高考数学复习不等式练习
考试要求：1、理解不等式的性质及其证明。2、掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用。3、掌握分析法、综合法、比较法证明简单的不等式。4、掌握简单不等式的解法。5、理解不等式：
1、若
为实数，则“
”是“
”的：
A．充分不必要条件 B．必要不充条件
C．充要条件 D．既不充分也不必要条件
2、设
的取值范围是：
A．
B．
C．
D．
3、设
、
分别是定义在R上的奇函数和偶函数，当
,
且
，则不等式
的解集是：
A.
B.
C.
D.
4、设函数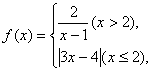
则使得
的自变量
的取值范围为
（A）
（B）
（C）
（D）
5、已知
，且
，则
、
的大小关系是
A. 
B. 
C. 
D. 不确定
6、下列命题中正确的是：
A. 
B.
C. 
D. 
7、若x<0，则2 + 3x + 的最大值是
8、已知a>b>0，那么a2 + 的最小值是
9、已知a,b
，且满足a
+ 3b = 1，则ab的最大值为___________________.
10、
是函数
恒为负值的___________条件
11、已知
是定义在R上的奇函数，当
时，
，那么不等式
的解集是
A.
B.
C. 
D．
12、若a，b∈R，则使 a + b >1成立的一个充分不必要条件是：
A． a + b ≥ 1 B． a ≥ 
且 b ≥ C．b <
D．a ≥ 1
13、设集合
，且
，那么实数a的取值范围是：
A．
B．
C．
D．
14、已知△ABC的三边长是a，b，c，且m为正数，求证 + > 。
15、已知函数
（1）判断函数
的增减性；
（2）若命题
为真命题，求实数x的取值范围.
16、已知函数
.
（1） 求
的值，使点
到直线
的距离最短为
；
（2） 若不等式
在
恒成立，求的取值范围.
三、不等式参考答案
1、A；2、A；3、D；4、D；5、A；6、B；7、
；8、16；9、
；
10、充分非必要；11、D；12、C；13、D
14、(略)
15、（1）
函数是
增函数；
（2）
，必有
时，
，不等式化为
故
;当
，
不等式化为
，这显然成立，此时
；
当
时，
，不等式化为
故
；综上所述知，使命题p为真命题的x的取值范围是
16、 解：（1）由题意得M到直线x + y
–1 = 0的距离
令
, 
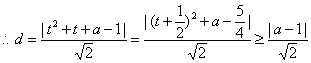
所以当
时，
，解得
或
（舍去），∴
（2）由
得
即
在恒成立. 也就是
在恒成立. 令
,则
, 即
在t∈[1，2]上恒成立
设
，则要使上述条件成立，只需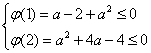
解得
, 即满足题意的a的取值范围是