高考数学复习二次函数测试题
1.(人教A版第27页A组第6题)解析式、待定系数法
若![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.
变式1:若二次函数![]() 的图像的顶点坐标为
的图像的顶点坐标为![]() ,与y轴的交点坐标为(0,11),则
,与y轴的交点坐标为(0,11),则
A.![]() B.
B.![]()
C.![]() D.
D.![]()
变式2:若![]() 的图像x=1对称,则c=_______.
的图像x=1对称,则c=_______.
变式3:若二次函数![]() 的图像与x轴有两个不同的交点
的图像与x轴有两个不同的交点![]() 、
、![]() ,且
,且![]() ,试问该二次函数的图像由
,试问该二次函数的图像由![]() 的图像向上平移几个单位得到?
的图像向上平移几个单位得到?
2.(北师大版第52页例2)图像特征
将函数![]() 配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.
配方,确定其对称轴,顶点坐标,求出它的单调区间及最大值或最小值,并画出它的图像.
变式1:已知二次函数![]() ,如果
,如果![]() (其中
(其中![]() ),则
),则![]()
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
 变式2:函数
变式2:函数![]() 对任意的x均有
对任意的x均有![]() ,那么
,那么![]() 、
、![]() 、
、![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
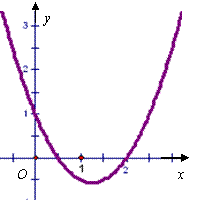
变式3:已知函数![]() 的图像如右图所示,
的图像如右图所示,
请至少写出三个与系数a、b、c有关的正确命题_________.
3.(人教A版第43页B组第1题)单调性
已知函数![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的单调区间;(2) 求
的单调区间;(2) 求![]() ,
,![]() 的最小值.
的最小值.
变式1:已知函数![]() 在区间
在区间![]() 内单调递减,则a的取值范围是
内单调递减,则a的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
变式2:已知函数![]() 在区间(,1)上为增函数,那么
在区间(,1)上为增函数,那么![]() 的取值范围是_________.
的取值范围是_________.
变式3:已知函数![]() 在
在![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围.
的取值范围.
4.(人教A版第43页B组第1题)最值
已知函数![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的单调区间;(2) 求
的单调区间;(2) 求![]() ,
,![]() 的最小值.
的最小值.
变式1:已知函数![]() 在区间[0,m]上有最大值3,最小值2,则m的取值范围是
在区间[0,m]上有最大值3,最小值2,则m的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
变式2:若函数![]() 的最大值为M,最小值为m,则M + m的值等于________.
的最大值为M,最小值为m,则M + m的值等于________.
变式3:已知函数![]() 在区间[0,2]上的最小值为3,求a的值.
在区间[0,2]上的最小值为3,求a的值.
5.(人教A版第43页A组第6题)奇偶性
已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() ≥0时,
≥0时,![]() .画出函数
.画出函数![]() 的图像,并求出函数的解析式.
的图像,并求出函数的解析式.
变式1:若函数![]() 是偶函数,则在区间
是偶函数,则在区间![]() 上
上![]() 是
是
A.增函数 B.减函数 C.常数 D.可能是增函数,也可能是常数
变式2:若函数![]() 是偶函数,则点
是偶函数,则点![]() 的坐标是________.
的坐标是________.
变式3:设![]() 为实数,函数
为实数,函数![]() ,
,![]() .
.
(I)讨论![]() 的奇偶性;(II)求
的奇偶性;(II)求![]() 的最小值.
的最小值.
6.(北师大版第64页A组第9题)图像变换
已知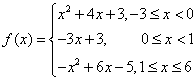 .
.
(1)画出函数的图象;(2)求函数的单调区间;(3)求函数的最大值和最小值.
变式1:指出函数![]() 的单调区间.
的单调区间.
变式2:已知函数![]() .
.
给下列命题:①![]() 必是偶函数;
必是偶函数;
②
当![]() 时,
时,![]() 的图像必关于直线x=1对称;
的图像必关于直线x=1对称;
③
若![]() ,则
,则![]() 在区间[a,+∞
在区间[a,+∞![]() 上是增函数;
上是增函数;
④![]() 有最大值
有最大值![]() .
.
其中正确的序号是________.③
变式3:设函数![]() 给出下列4个命题:
给出下列4个命题:
①当c=0时,![]() 是奇函数;
是奇函数;
②当b=0,c>0时,方程![]() 只有一个实根;
只有一个实根;
③![]() 的图象关于点(0,c)对称;
的图象关于点(0,c)对称;
④方程![]() 至多有两个实根.
至多有两个实根.
上述命题中正确的序号为 .
7.(北师大版第54页A组第6题)值域
求二次函数![]() 在下列定义域上的值域:
在下列定义域上的值域:
(1)定义域为![]() ;(2) 定义域为
;(2) 定义域为![]() .
.
变式1:函数![]() 的值域是
的值域是
A.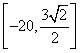 B.
B.![]() C.
C.![]() D.
D. ![]()
变式2:函数y=cos2x+sinx的值域是__________.
变式3:已知二次函数 f (x) = a x 2 + bx(a、b 为常数,且 a ≠ 0),满足条件 f (1 + x) = f (1-x),且方程 f (x) = x 有等根.
(1)求 f (x) 的解析式;
(2)是否存在实数 m、n(m < n),使 f (x) 的定义域和值域分别为 [m,n] 和 [3m,3n],如果
存在,求出 m、n 的值,如果不存在,说明理由.
8.(北师大版第54页B组第5题)恒成立问题
当![]() 具有什么关系时,二次函数
具有什么关系时,二次函数![]() 的函数值恒大于零?恒小于零?
的函数值恒大于零?恒小于零?
变式1:已知函数 f (x) = lg (a x 2 + 2x + 1) .
(I)若函数 f (x) 的定义域为 R,求实数 a 的取值范围;
(II)若函数 f (x) 的值域为 R,求实数 a 的取值范围.
变式2:已知函数![]() ,若
,若![]() 时,有
时,有![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
变式3:若f (x) = x 2 + bx + c,不论 a、b 为何实数,恒有 f (sin a )≥0,f (2 + cos b )≤0.
(I) 求证:b + c = -1;
(II) 求证: c≥3;
(III) 若函数 f (sin a ) 的最大值为 8,求 b、c 的值.
9.(北师大版第54页B组第1题)根与系数关系
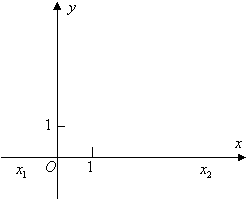 右图是二次函数
右图是二次函数![]() 的图像,它与x轴交于点
的图像,它与x轴交于点![]() 和
和![]() ,试确定
,试确定![]() 以及
以及![]() ,
,![]() 的符号.
的符号.
变式1:二次函数![]() 与一次函数
与一次函数![]() 在同一个直角坐标系的图像为
在同一个直角坐标系的图像为

变式2:直线![]() 与抛物线
与抛物线![]()
![]()
![]() 中至少有一条相交,则m的取值范围是.
中至少有一条相交,则m的取值范围是.
变式3:对于函数 f (x),若存在 x0 Î R,使 f (x0) = x0 成立,则称 x0 为 f (x) 的不动点.如果函数 f (x) = a x 2 + bx + 1(a > 0)有两个相异的不动点 x1、x2.
(I)若 x1 < 1 < x2,且 f (x) 的图象关于直线 x = m 对称,求证m > ;
(II)若 x1 < 2 且 x1-x2 = 2,求 b 的取值范围.
10.(北师大版第52页例3)应用
绿缘商店每月按出厂价每瓶3元购进一种饮料.根据以前的统计数据,若零售价定为每瓶4元,每月可销售400瓶;若每瓶售价每降低0.05元,则可多销售40瓶.在每月的进货量当月销售完的前提下,请你给该商店设计一个方安:销售价应定为多少元和从工厂购进多少瓶时,才可获得最大的利润?
 变式1:在抛物线
变式1:在抛物线![]() 与x轴所围成图形的内接矩形(一边在x轴上)中(如图),求周长最长的内接矩形两边之比,其中a是正实数.
与x轴所围成图形的内接矩形(一边在x轴上)中(如图),求周长最长的内接矩形两边之比,其中a是正实数.
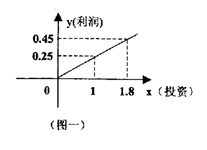
变式2:某民营企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图一;B产品的利润与投资的算术平方根成正比,其关系如图二(注:利润和投资单位:万元)
(1)
 分别将A、B两种产品的利润表示为投资的函数关系式;
分别将A、B两种产品的利润表示为投资的函数关系式;
(2)
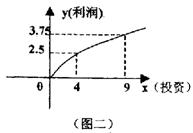 该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润?其最大利润约为多少元(精确到1万元)?
该企业已筹集到10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润?其最大利润约为多少元(精确到1万元)?
变式3:设a为实数,记函数![]() 的最大值为g(a) .
的最大值为g(a) .
(Ⅰ)求g(a);(Ⅱ)试求满足![]() 的所有实数a.
的所有实数a.
二次函数答案
1.(人教A版第27页A组第6题)解析式、待定系数法
变式1: 解:由题意可知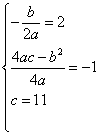 ,解得
,解得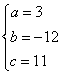 ,故选D.
,故选D.
变式2: 解:由题意可知![]() ,解得b=0,∴
,解得b=0,∴![]() ,解得c=2.
,解得c=2.
变式3:解:由题意可设所求二次函数的解析式为![]() ,
,
展开得![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
所以,该二次函数的图像是由![]() 的图像向上平移 单位得到的,它的解析式是
的图像向上平移 单位得到的,它的解析式是![]() ,即
,即![]() .
.
2.(北师大版第52页例2)图像特征
变式1: 解:根据题意可知![]() ,∴
,∴ ![]()
![]() ,故选D.
,故选D.
变式2: 解:∵![]() ,∴抛物线
,∴抛物线![]() 的对称轴是
的对称轴是![]() ,
,
∴ ![]() 即
即![]() ,
,
∴![]() ,∴
,∴![]() 、
、![]() 、
、![]() ,
,
 故有
故有![]() ,选C.
,选C.
变式3: 解:观察函数图像可得:
① a>0(开口方向);② c=1(和y轴的交点);
③ ![]() (和x轴的交点);④
(和x轴的交点);④![]() (
(![]() );
);
⑤ ![]() (判别式);⑥
(判别式);⑥ ![]() (对称轴).
(对称轴).
3.(人教A版第43页B组第1题)单调性
变式1: 解:函数![]() 图像是开口向上的抛物线,其对称轴是
图像是开口向上的抛物线,其对称轴是![]() ,
,
由已知函数在区间![]() 内单调递减可知区间
内单调递减可知区间![]() 应在直线
应在直线![]() 的左侧,
的左侧,
∴![]() ,解得
,解得![]() ,故选D.
,故选D.
变式2:解:函数![]() 在区间(,1)上为增函数,由于其图像(抛物线)开口向上,所以其对称轴
在区间(,1)上为增函数,由于其图像(抛物线)开口向上,所以其对称轴![]() 或与直线
或与直线![]() 重合或位于直线
重合或位于直线![]() 的左侧,即应有
的左侧,即应有![]() ,解得
,解得![]() ,
,
∴ ![]() ,即
,即![]() .
.
变式3:解:函数![]() 的图像是开口向下的抛物线,经过坐标原点,对称轴是
的图像是开口向下的抛物线,经过坐标原点,对称轴是![]() ,
,
∵ 已知函数在![]() 上是单调函数,∴ 区间
上是单调函数,∴ 区间![]() 应在直线
应在直线![]() 的左侧或右侧,
的左侧或右侧,
 即有
即有![]() 或
或![]() ,解得
,解得![]() 或
或![]() .
.
4.(人教A版第43页B组第1题)最值
变式1: 解:作出函数![]() 的图像,
的图像,
开口向上,对称轴上x=1,顶点是(1,2),和y轴的交点是(0,3),
∴m的取值范围是![]() ,故选C.
,故选C.
变式2: 解:函数有意义,应有![]() ,解得
,解得![]() ,
,
∴ ![]() Þ
Þ ![]() Þ
Þ ![]() ,
,
∴ M=6,m=0,故M + m=6.
变式3: 解:函数![]() 的表达式可化为
的表达式可化为![]() .
.
① 当![]() ,即
,即![]() 时,
时,![]() 有最小值
有最小值![]() ,依题意应有
,依题意应有![]() ,解得
,解得![]() ,这个值与
,这个值与![]() 相矛盾.
相矛盾.
②当![]() ,即
,即![]() 时,
时,![]() 是最小值,依题意应有
是最小值,依题意应有![]() ,解得
,解得![]() ,又∵
,又∵![]() ,∴
,∴![]() 为所求.
为所求.
③当![]() ,即
,即![]() 时,
时,![]() 是最小值,
是最小值,
依题意应有![]() ,解得
,解得![]() ,又∵
,又∵![]() ,∴
,∴![]() 为所求.
为所求.
综上所述,![]() 或
或![]() .
.
5.(人教A版第43页A组第6题)奇偶性
变式1: 解:函数![]() 是偶函数 Þ
是偶函数 Þ ![]() Þ
Þ ![]() ,
,
当![]() 时,
时,![]() 是常数;当
是常数;当![]() 时,
时,![]() ,在区间
,在区间![]() 上
上![]() 是增函数,故选D.
是增函数,故选D.
变式2:解:根据题意可知应有![]() 且
且![]() ,即
,即![]() 且
且![]() ,∴点
,∴点![]() 的坐标是
的坐标是![]() .
.
变式3: 解:(I)当![]() 时,函数
时,函数![]() ,此时,
,此时,![]() 为偶函数;
为偶函数;
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() ,此时
,此时![]() 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(II)(i)当![]() 时,
时,![]() ,
,
若![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,从而函数
上单调递减,从而函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
若![]() ,则函数
,则函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,且
,且![]() .
.
(ii)当![]() 时,函数
时,函数![]() ,
,
若![]() ,则函数
,则函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,且
,且![]() ,
,
若![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,从而函数
上单调递增,从而函数![]() 在
在![]() 上的最小值为
上的最小值为![]() .
.
综上,当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() .
.
6.(北师大版第64页A组第9题)图像变换
变式1: 解:函数可转化为二次函数,作出函数图像,由图像可得单调区间.
 当
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
作出函数图像,由图像可得单调区间.
在![]() 和
和![]() 上,函数是增函数;在
上,函数是增函数;在![]() 和
和![]() 上,函数是减函数.
上,函数是减函数.
变式2:
解:若![]() 则
则![]() ,显然不是偶函数,所以①是不正确的;
,显然不是偶函数,所以①是不正确的;
若![]() 则
则![]() ,满足
,满足![]() ,但
,但![]() 的图像不关于直线x=1对称,所以②是不正确的;
的图像不关于直线x=1对称,所以②是不正确的;
若![]() ,则
,则![]() ,图像是开口向上的抛物线,其对称轴是
,图像是开口向上的抛物线,其对称轴是![]() ,∴
,∴![]() 在区间[a,+∞
在区间[a,+∞![]() 上是增函数,即③是正确的;
上是增函数,即③是正确的;
显然函数![]() 没有最大值,所以④是不正确的.
没有最大值,所以④是不正确的.
变式3: 解: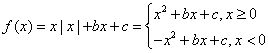 ,
,
(1)当c=0时,![]() ,满足
,满足![]() ,是奇函数,所以①是正确的;
,是奇函数,所以①是正确的;
(2)当b=0,c>0时,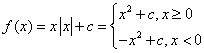 ,
,
方程![]() 即
即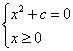 或
或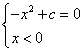 ,
,
显然方程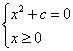 无解;方程
无解;方程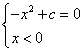 的唯一解是
的唯一解是![]() ,所以② 是正确的;
,所以② 是正确的;
(3)设![]() 是函数
是函数![]() 图像上的任一点,应有
图像上的任一点,应有![]() ,
,
而该点关于(0,c)对称的点是![]() ,代入检验
,代入检验![]() 即
即![]() ,也即
,也即![]() ,所以
,所以![]() 也是函数
也是函数![]() 图像上的点,所以③是正确的;
图像上的点,所以③是正确的;
(4)若![]() ,则
,则![]() ,显然方程
,显然方程![]() 有三个根,所以④ 是不正确的.
有三个根,所以④ 是不正确的.
7.(北师大版第54页A组第6题)值域
变式1: 解:作出函数![]() 的图象,容易发现在
的图象,容易发现在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,求出
上是减函数,求出![]() ,
,![]() ,
,![]() ,注意到函数定义不包含
,注意到函数定义不包含![]() ,所以函数值域是
,所以函数值域是![]() .
.
变式2:解:∵ y= cos2x+sinx=-2sin2x+sinx+1,令t= sinx Î [-1,1],
则y=-2t2+t+1,其中tÎ [-1,1],
∴y Î [-2, ],即原函数的值域是[-2, ].
变式3: 解:(I) ∵ f (1 + x) = f (1-x),
∴ - = 1,
又方程 f (x) = x 有等根 Û a x 2 + (b-1) x = 0 有等根,
∴ △= (b-1) 2 = 0 Þ b = 1 Þ a = -,
∴ f (x) = -x 2 + x.
(II) ∵ f (x) 为开口向下的抛物线,对称轴为 x = 1,
1° 当 m≥1 时,f (x) 在 [m,n] 上是减函数,
∴ 3m = f (x)min = f (n) = -n 2 + n (*),
3n = f (x)max = f (m) = -m 2 + m,
两式相减得:3 (m-n) = -(n 2-m 2) + (n-m),
∵ 1≤m < n,上式除以 m-n 得:m + n = 8,
代入 (*) 化简得:n 2-8n + 48 = 0 无实数解.
2° 当 n≤1 时,f (x) 在 [m,n] 上是增函数,
∴ 3m = f (x)min = f (m) = -m 2 + m,
3n = f (x)max = f (n) = -n 2 + n,
∴ m = -4,n = 0.
3° 当 m≤1≤n 时,对称轴 x = 1 Î [m,n],
∴ 3n = f (x)max = f (1) = Þ n = 与 n≥1 矛盾.
综合上述知,存在 m = -4、n = 0 满足条件.
8.(北师大版第54页B组第5题)恒成立问题
变式1: 解:(I) 函数 f (x) 的定义域为 R,即不等式a x 2 + 2x + 1 > 0 的解集为 R,
∴应有 Þ a > 1,
∴ 实数 a 的取值范围是(1,+¥) .
(II) 函数 f (x) 的值域为 R,即a x 2 + 2x + 1 能够取 (0,+¥) 的所有值.
1° 当 a = 0 时,a x 2 + 2x + 1 = 2x + 1满足要求;
2° 当 a ≠ 0 时,应有 Þ 0 < a≤1.
∴ 实数 a 的取值范围是[0,1] .
变式2: 解法一:(转化为最值)
![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
⑴![]() ,
, ![]() ;
;
⑵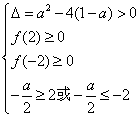 ,
,![]() .
.
综上所述![]() .
.
解法二:(运用根的分布)
⑴当![]() ,即
,即![]() 时,应有
时,应有![]() , 即
, 即![]() ,
,![]() 不存在;
不存在;
⑵当![]() ,即
,即![]() 时,应有
时,应有![]() ,
,
即![]() ,
,![]() ;
;
⑶当![]() ,即
,即![]() 时,应有
时,应有![]() ,即
,即![]() ,
, ![]()
综上所述![]() .
.
变式3: 证明:(I) 依题意,f (sin ) = f (1)≥0,f (2 + cos p) = f (1)≤0,
∴ f (1) = 0 Þ 1 + b + c = 0 Þ b + c = -1,
(II) 由 (I) 得: f (x) = x 2-(c + 1) x + c (*)
∵ f (2 + cos b )≤0 Þ (2 + cos b ) 2-(c + 1) (2 + cos b ) + c≤0
Þ (1 + cos b ) [c-(2 + cos b )]≥0,对任意 b 成立.
∵ 1 + cos b ≥0 Þ c≥2 + cos b ,
∴ c≥(2 + cos b )max = 3.
(III) 由 (*) 得:f (sin a ) = sin 2a-(c + 1) sin a + c,
设 t = sin a ,则g(t) = f (sin a ) = t 2-(c + 1) t + c,-1≤t≤1,
这是一开口向上的抛物线,对称轴为 t = ,
由 (II) 知:t≥= 2,
∴ g(t) 在 [-1,1] 上为减函数.
∴ g(t)max = g(-1) = 1 + (c + 1) + c = 2c + 2 = 8,
∴ c = 3
∴ b = -c-1 = -4.
9.(北师大版第54页B组第1题)根与系数关系
变式1: 解:二次函数![]() 与一次函数图象
与一次函数图象![]() 交于两点
交于两点![]() 、
、![]() ,由二次函
,由二次函
数图象知![]() 同号,而由
同号,而由![]() 中一次函数图象知
中一次函数图象知![]() 异号,互相矛盾,故舍去
异号,互相矛盾,故舍去![]() .
.
又由![]() 知,当
知,当![]() 时,
时,![]() ,此时与
,此时与![]() 中图形不符,当
中图形不符,当![]() 时,
时,![]() ,与
,与![]() 中图形相符.
中图形相符.
变式2: 解:原命题可变为:求方程![]() ,
,![]() ,
,
![]() 中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的
中至少有一个方程有实数解,而此命题的反面是:“三个方程均无实数解”,于是,从全体实数中除去三个方程均无实数解的![]() 的值,即得所求.
的值,即得所求.
解不等式组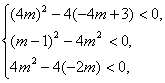 得
得 ![]() ,
,
故符合条件的![]() 取值范围是
取值范围是![]() 或
或![]() .
.
变式3: 解:(I) 由 f (x) 表达式得 m = -,
∵ g(x) = f (x)-x = a x 2 + (b-1) x + 1,a > 0,
由 x1,x2 是方程 f (x) = x的两相异根,且 x1 < 1 < x2,
∴ g(1) < 0 Þ a + b < 0 Þ -> 1 Þ -> ,即 m > .
(II) △= (b-1) 2-4a > 0 Þ (b-1) 2 > 4a,
x1 + x2 = ,x1x2 = ,
∴ x1-x2 2 = (x1 + x2) 2-4x1x2 = () 2-= 2 2,
∴ (b-1) 2 = 4a + 4a 2 (*)
又 x1-x2 = 2,
∴ x1、x2 到 g(x) 对称轴 x = 的距离都为1,
要 g(x) = 0 有一根属于 (-2,2),
则 g(x) 对称轴 x = Î (-3,3),
∴ -3 < < 3 Þ a > b-1 ,
把代入 (*) 得:(b-1) 2 > b-1 + (b-1) 2,
解得:b < 或 b > ,
∴ b 的取值范围是:(-¥, )∪( ,+¥).
10.(北师大版第52页例3)应用
变式1: 解:设矩形ABCD在x轴上的边是BC,BC的长是x(0<x<a),
则B点的坐标为![]() ,A点的坐标为
,A点的坐标为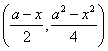 .
.
设矩形ABCD的周长为P,
则P=2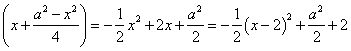 (0<x<a).
(0<x<a).
① 若a>2,则当x=2时,矩形的周长P有最大值,这时矩形两边的长分别为2和![]() ,两边之比为8:
,两边之比为8:![]() ;
;
②若0 <a≤2,此时函数P=![]() 无最大值,也就是说周长最大的内接矩形不存在.
无最大值,也就是说周长最大的内接矩形不存在.
综上所述,当a>2时,周长最大的内接矩形两边之比为8:![]() ;当0 <a≤2时,周长最大的内接矩形不存在.
;当0 <a≤2时,周长最大的内接矩形不存在.
变式2: 解:(I) 依题意设 A、B 两种产品的利润表示为投资的函数关系式分别为
f (x) = kx,g(x) = m,
由 f (1) = k = 0.25, g(4) = 2m = 2.5 Þ m = ,
∴ f (x) = x(x≥0),g(x) = .
(II) 设企业在 B 产品投资 x 万元,则在 A 产品投资 10-x 万元,
∴ 企业的利润 y = (10-x) + = [-(-) 2 + ](0≤x≤10),
∴ = ,即 x = 6.25 万元时,企业获得最大利润 ≈4 万元.
答:在 A 产品投资 3.75 万元,在 B 产品投资 6.25 万元,企业获得最大利润约 4 万元.
变式3:
解:设![]() ,要使
,要使![]() 有意义,必须
有意义,必须![]() 且
且![]() ,即
,即![]() ,
,
∵![]() ,且
,且![]() ……①
……①
∴![]() 的取值范围是
的取值范围是![]() .
.
由①得:![]() ,
,
不妨设![]()
![]() ,
,![]() .
.
(I)由题意知![]() 即为函数
即为函数![]()
![]() ,
,![]() 的最大值,
的最大值,
当![]() 时,
时,![]() ,
,![]() ,有
,有![]() =2;
=2;
当![]() 时,此时直线
时,此时直线![]() 是抛物线
是抛物线![]()
![]() 的对称轴,
的对称轴,
∴可分以下几种情况进行讨论:
(1)当![]() 时,函数
时,函数![]() ,
,![]() 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由![]() 知
知![]() 在
在![]() 上单调递增,故
上单调递增,故![]()
![]()
![]() ;
;
(2)当![]() 时,,函数
时,,函数![]() ,
,![]() 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若![]()
![]() 即
即![]() 时,
时,![]()
![]() ,
,
若![]()
![]() 即
即![]() 时,
时,![]()
![]() ,
,
若![]()
![]() 即
即![]() 时,
时,![]()
![]()
![]() .
.
综上所述,有![]() =
=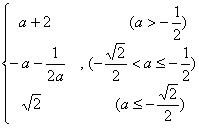 .
.
(II)若a>0,则>0,此时g(a)=g( ) Û a+2= +2 Û a = Þa =1(舍去a=-1);
若-<a<0,则<-2,此时g(a)=g( ) Û a+2=Þ a=-2+<-(舍去);
若-<a≤-,则-2≤<-,
此时g(a)=g( ) Û -a-= Þ a=- (舍去);
若-≤a≤-,则-≤≤-,
此时g(a)=g( ) Û =恒成立;
若-2≤a<-,则-<≤-,
此时g(a)=g( ) Û =-a-Þ a=- (舍去);
若a<-2,则-<<0,
此时g(a)=g( ) Û = a+2Þ a=-2+>-2 (舍去) .
综上所述,满足![]() 的所有实数a为:
的所有实数a为:![]() 或
或![]() .
.