高考数学复习导数变式题(命题人:广大附中 王映)
一 导数的概念与运算
1。如果质点A按规律s=2t3运动,则在t=3 s时的瞬时速度为( )
A. 6m/s B. 18m/s C. 54m/s D. 81m/s
解析:∵s′=6t2,∴s′t=3=54. 答案:C
变式:定义在D上的函数![]() ,如果满足:
,如果满足:![]() ,
,![]() 常数
常数![]() ,都有
,都有![]() ≤M成立,则称
≤M成立,则称![]() 是D上的有界函数,其中M称为函数的上界.
是D上的有界函数,其中M称为函数的上界.
文(1)若已知质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
理(2)若已知质点的运动方程为![]() ,要使在
,要使在![]() 上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
上的每一时刻的瞬时速度是以M=1为上界的有界函数,求实数a的取值范围.
解: (1) ∵![]() . 由
. 由![]() ≤1,得
≤1,得![]() ≤1
≤1
∴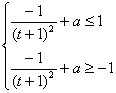
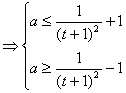
令![]() ,显然
,显然![]() 在
在![]() 上单调递减,
上单调递减,
则当t→+∞时,![]() →1. ∴
→1. ∴![]()
令![]() ,显然
,显然![]() 在
在![]() 上单调递减,
上单调递减,
则当![]() 时,
时,![]() ∴
∴![]()
∴0≤a≤1;
故所求a的取值范围为0≤a≤1.
(2)∵![]() . 由
. 由![]() ≤1,得
≤1,得![]() ≤1
≤1
∴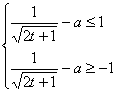
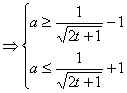
令![]() ,则
,则![]() .
.
当![]() 时,有
时,有![]() ,
,
∴![]() 在[0,+∞
在[0,+∞![]() 上单调递减.
上单调递减.
故当t=0 时,有![]() ;
;
又![]() ,当t→+∞时,
,当t→+∞时,![]() →0,
→0,
∴ ![]() ,从而有
,从而有![]() ≤0,且
≤0,且![]() . ∴0≤a≤1;
故所求a的取值范围为0≤a≤1.
. ∴0≤a≤1;
故所求a的取值范围为0≤a≤1.
2.已知![]() 的值是( )
的值是( )
A.
![]() B.
2 C.
B.
2 C. ![]() D. -2
D. -2
解:
![]()
得![]() 选A
选A
变式1:![]() ( )
( )
A.-1 B.-2 C.-3 D.1
解:
![]() .
.
选B.
变式2:![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
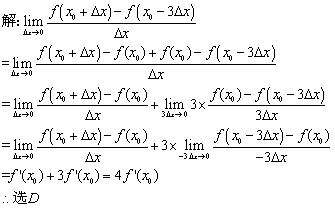
3.人教版选修1-1第84页例2,选修2-2第8页例2:
根据所给的函数图像比较![]()
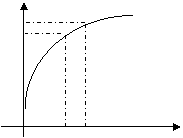
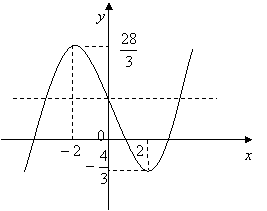
变式:函数![]() 的图像如图所示,下列数值排序正确的是( )
的图像如图所示,下列数值排序正确的是( )
 A.
A. ![]() y
y
B. ![]()
C. ![]()
D. ![]() O 1
2 3 4 x
O 1
2 3 4 x
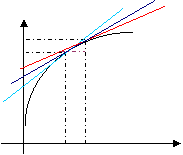
解:设x=2,x=3时曲线上的点为A、B,点A处的切线为AT
点B处的切线为BQ, T
![]()
![]() y
B
y
B
![]()
![]() A
A
如图所示,切线BQ的倾斜角小于
直线AB的倾斜角小于 Q
切线AT的倾斜角
![]()
![]()
![]() O 1 2
3 4 x
O 1 2
3 4 x
所以选B
4.人教版选修1-1第93页习题A组第4题,选修2-2第18页习题A组第4题,
求所给函数的导数:
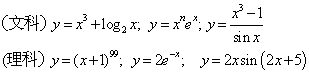 。
。
变式:
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,![]() >0.
>0.
且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A.(-3,0)∪(3,+∞) B.(-3,0)∪(0, 3)
C.(-∞,- 3)∪(3,+∞) D.(-∞,- 3)∪(0, 3)

5.人教版选修1-1第93页A组第6题、选修2-2第18页A组第6题
已知函数![]() .(1)求这个函数的导数;(2)求这个函数在点
.(1)求这个函数的导数;(2)求这个函数在点![]() 处的切线的方程.
处的切线的方程.
变式1:已知函数![]() .(1)求这个函数在点
.(1)求这个函数在点![]() 处的切线的方程;
处的切线的方程;
(2)过原点作曲线y=ex的切线,求切线的方程.
解:(1)依题意得:切点为![]() ,
,
由点斜式得切线方程![]() ,
,
即![]() .
.
(2)
设切点为![]()
由点斜式得![]() ,
,
![]() 切线过原点,
切线过原点,![]()
切点为![]()
![]() 由点斜式,得:
由点斜式,得:![]() 即:
即:![]()
变式2:函数y=ax2+1的图象与直线y=x相切,则a=( )
A.
![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
解:设切点为![]() ①
①
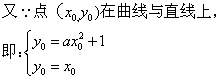 ②
②
由①、②得![]() ,选B
,选B
说明:1.在“某点处的切线”与“过某点的切线”意义不同,注意审题,后者一定要先“设切点的坐标” 2.求切线方程的步骤是:(1)明确切点;(2)确定该点处的切线的斜率(即该点处的导数值);(3)若切点不明确,则应考虑先设切点.
6.人教版选修1-1第99页例2选修2-2第25页例2
判断下列函数的单调性,并求出单调区间:
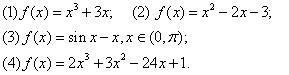
变式1:函数![]() 的一个单调递增区间是
的一个单调递增区间是
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
解:![]()
![]()
![]() ,选A
,选A
或![]() (理科要求:复合函数求导)
(理科要求:复合函数求导)
变式2:(1) 已知函数![]() (1)若函数的单调递减区间是(-3,1),则
(1)若函数的单调递减区间是(-3,1),则![]() 的值是
. (2)若函数在
的值是
. (2)若函数在![]() 上是单调增函数,则
上是单调增函数,则![]() 的取值范围是
.
的取值范围是
.
解: (1)若函数的单调递减区间是(-3,1)![]() ,(2) 若函数在
,(2) 若函数在![]() 上是单调增函数
上是单调增函数 ![]()
解:(1)![]() ,因为函数的单调递减区间是(-3,1)
,因为函数的单调递减区间是(-3,1)![]() ,
,
所以-3,1是方程![]() 的两个实数根,由韦达定理,
的两个实数根,由韦达定理,![]() (草图略)
(草图略)
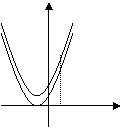 (2)若函数在
(2)若函数在![]() 上是单调增函数
上是单调增函数![]() ,
,
如图示,分类讨论:
① 当![]() 即
即![]() 即
即![]() 条件成立;
条件成立;
②  当
当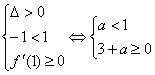 ,即
,即 ![]() 条件成立;
条件成立;
综上,![]() 条件成立,
条件成立,![]() 为所求.
为所求.
变式3: 设![]() ,点P(
,点P(![]() ,0)是函数
,0)是函数![]() 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用![]() 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数![]() 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求![]() 的取值范围.
的取值范围.
解:(I)因为函数![]() ,
,![]() 的图象都过点(
的图象都过点(![]() ,0),所以
,0),所以![]() ,
,
即![]() .因为
.因为![]() 所以
所以![]() .
.
![]()
又因为![]() ,
,![]() 在点(
在点(![]() ,0)处有相同的切线,所以
,0)处有相同的切线,所以![]()
而![]()
将![]() 代入上式得
代入上式得![]() 因此
因此![]() 故
故![]() ,
,![]() ,
,![]()
(II)解法一![]() .
.
当![]() 时,函数
时,函数![]() 单调递减.
单调递减.
由![]() ,若
,若![]() ;若
;若![]()
由题意,函数![]() 在(-1,3)上单调递减,则
在(-1,3)上单调递减,则
![]()
所以![]()
所以![]() 的取值范围为
的取值范围为![]()
解法二:![]()
因为函数![]() 在(-1,3)上单调递减,且
在(-1,3)上单调递减,且![]() 是(-1,3)
是(-1,3)
上的抛物线,
所以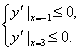 即
即![]() 解得
解得![]()
所以![]() 的取值范围为
的取值范围为![]()
7.人教版选修1-1第103页例4 ,选修2-2第29页例4
求函数![]() 的极值.
的极值.
人教版选修1-1第106页例5 ,选修2-2第32页例5
求函数![]() 在
在![]() 上的最大值与最小值..
上的最大值与最小值..
变式1:
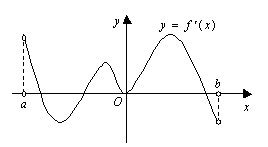 函数
函数![]() 的定义域为开区间
的定义域为开区间![]() ,导函数
,导函数![]() 在
在![]() 内的图象如图所示,则函数
内的图象如图所示,则函数![]() 在开区间
在开区间![]() 内有极小值点( )
内有极小值点( )
A.1个
B.2个
C.3个
D.4个
解:注意审题,题目给出的是导函数的图像。先由导函数取值的正负确定函数的单调性,然后列表可判断函数极小值点的个数。选A
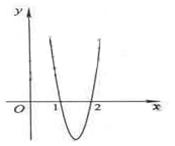 变式2:已知函数
变式2:已知函数![]() 在点
在点![]() 处取得极大值
处取得极大值![]() ,其导函数
,其导函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,如图所示.求:
,如图所示.求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ)![]() 的值.
的值.
解:
(Ⅰ)由图得
| X | (0,1) | 1 | (1,2) | 2 | |
|
| | 0 |
| 0 |
|
|
|
| 极大值 |
| 极小值 |
|
则![]() =1;
=1;
(Ⅱ)依题意得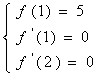 即
即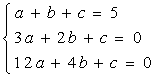
![]()
![]() .
.
变式3:
若函数![]() ,当
,当![]() 时,函数
时,函数![]() 有极值
有极值![]() ,
,
(1)求函数的解析式;
(2)若函数![]() 有3个解,求实数
有3个解,求实数![]() 的取值范围.
的取值范围.
解:![]()
(1) 由题意:
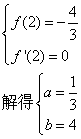
![]() 所求解析式为
所求解析式为![]()
(2)由(1)可得:![]()
令![]() ,得
,得![]() 或
或![]()
当![]() 变化时,
变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
| — |
|
|
|
| 单调递增↗ |
| 单调递减↘ |
| 单调递增↗ |
因此,当![]() 时,
时,![]() 有极大值
有极大值![]()
 当
当![]() 时,
时,![]() 有极小值
有极小值![]()
![]() 函数
函数![]() 的图象大致如图:……13分
y=k
的图象大致如图:……13分
y=k
由图可知:![]()
变式4:已知函数![]() ,对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
,对xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范围。
解:
f¢(x)=3x2-x-2=(3x+2)(x-1),函数f(x)的单调区间如下表:
| X | (-¥,- | - | (- | 1 | (1,+¥) |
| f¢(x) | + | 0 | - | 0 | + |
| f(x) | | 极大值 | ¯ | 极小值 | |
f(x)=x3-![]() x2-2x+c,xÎ〔-1,2〕,当x=-
x2-2x+c,xÎ〔-1,2〕,当x=-![]() 时,f(x)=
时,f(x)=![]() +c为极大值,
+c为极大值,
而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)<c2(xÎ〔-1,2〕)恒成立,只需c2>f(2)=2+c
解得c<-1或c>2
三、导数的在研究函数中的应用及生活中的优化问题
8.人教版选修1-1第108页B 组习题,选修2-2第34页B组习题
利用函数的单调性,证明:![]()
变式1:证明:![]() ,
,![]()
证明:(1)构造函数![]() ,
,
![]()
![]() ,当
,当![]()
![]() ,得下表
,得下表
|
|
|
| |
|
| + | 0 | — |
|
| 单调递增 | 极大值 | 单调递减 |
![]() 总有
总有![]()
![]()
![]()
另解![]()
![]() ,当
,当![]()
![]() ,
,
当![]() ,
,![]() 单调递增,
单调递增,![]() ……①
……①
当![]() ,
,![]() 单调递减,
单调递减,![]() ………………②
………………②
当![]()
![]() …………………………………………………………③
…………………………………………………………③
综合①②③得:当![]() 时,
时,![]()
![]()
![]()
(2)构造函数![]()
![]() ,
,
当![]()
![]() ,当
,当![]()
![]() 单调递减;
单调递减;
当![]()
![]() 单调递增;
单调递增;![]() 极小值=
极小值=![]() ,
,
![]() 总有
总有![]()
![]() 即:
即:![]() .
.
综上(1)(2)不等式![]() 成立.
成立.
变式:(理科)设函数f(x)=(1+x)2-ln(1+x)2.若关于x的方程f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,求实数a的取值范围.
解:
方程f(x)=x2+x+a, 即x-a+1-ln(1+x)2=0,记g(x)=x-a+1-ln(1+x)2.
所以![]() .由
.由![]() >0,得x<-1或x>1,由
>0,得x<-1或x>1,由![]() <0
<0
得-1<x<1.
所以g(x)在[0,1]上递减,在[1,2]上递增,为使f(x)=x2+x+a在[0,2]上恰好有两个相异的实根,只须g(x)=0在![]() 上各有一个实根,于是有
上各有一个实根,于是有
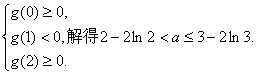
9. 函数![]() 若
若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
解:由![]() ,得
,得![]()
![]() 单调递增;
单调递增;
又![]()
![]()
![]() ,
,
所以![]() 是奇函数.
是奇函数.![]()
![]() ,
,
![]()
![]() 在
在![]() 上单调递增,
上单调递增, ![]() 恒成立,即:
恒成立,即:![]() 恒成立,分类:①当
恒成立,分类:①当![]() 恒成立,
恒成立,![]() 适合;
适合;
②当![]()
![]() 恒成立
恒成立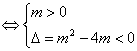 解得:
解得:![]()
综上,![]()
说明:(1)通过研究函数的性质(单调性与奇偶性),利用函数的性质解决不等式问题,是函数思想的重要应用.(2)找寻使![]() 恒成立的条件实际上依然用的是函数图像(数形结合)的函数思想.
恒成立的条件实际上依然用的是函数图像(数形结合)的函数思想.
变式:设函数![]() 若
若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:由![]() ,得
,得![]()
![]() 单调递增;
单调递增;
又![]()
![]()
![]() ,
,
所以![]() 是奇函数.
是奇函数.![]() ,
,
![]() 恒成立,即
恒成立,即![]() 恒成立.
恒成立.
①当![]() 成立;
成立;![]() ②当
②当![]()
![]()
![]()
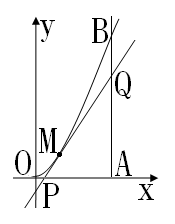
10.如图,曲线段OMB是函数![]() 的图象,
的图象,![]() 轴于点A,曲线段OMB上一点M
轴于点A,曲线段OMB上一点M![]() 处的切线PQ交x轴于点P,交线段AB于点Q
处的切线PQ交x轴于点P,交线段AB于点Q
(1)若t已知,求切线PQ的方程 (2)求![]() 的面积的最大值
的面积的最大值
 解:(1)
解:(1)![]() ,所以过点M的切线的斜率为
,所以过点M的切线的斜率为![]()
由点斜式得切线PQ方程为![]() ,
,
即![]() ……①
……①
(2)![]() …………②
…………②
对①令x=6得![]() …………③
…………③
令y=0得![]() …………④
…………④
③④代入②得![]()
![]() ,令
,令![]() 解得
解得![]()
| T | (0,4) | 4 | (4,6) |
| S’ | + | 0 | - |
| S | 增 | 极大值64 | 减 |
所以当t=4时![]() 有极大值64,
有极大值64,
所以当t=4时,![]() 的面积的最大值为64.
的面积的最大值为64.
11.用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻折900角,再焊接而成,问该容器的高为多少时,容器的容积最大?最大的容积是多少?
解:设容器的高为x,容器的体积为V.
则![]() (0 < x < 24)
(0 < x < 24)
=![]() x
x
∵![]() x
x
由![]()
∴![]()
所以 当![]()
又![]()
所以 ![]() 0
0
答:该容器的高为10cm时,容器有最大容积19600![]()
12.某厂生产某种产品![]() 件的总成本
件的总成本![]() (万元),已知产品单价的平方与产品件数
(万元),已知产品单价的平方与产品件数![]() 成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
成反比,生产100件这样的产品单价为50万元,产量定为多少时总利润最大?
分析:先建立总利润的目标函数,总利润=总销售量-总成本C(x)= 产品件数*产品单价-C(x),因而应首先求出产品单价P(x)的解析式.
解:设产品的单价P元,据已知,![]() ,
,
![]()
![]() 设利润为y万元,则
设利润为y万元,则
![]()
![]()
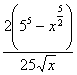 ,
,![]()
![]() 递增;
递增;![]() 递减,
递减,
![]() 极大=
极大=![]() 最大.
最大.
答:当产量为25万件时,总利润最大
四、理科定积分、微积分
选修2-2第59页例1、例2
计算下列定积分:
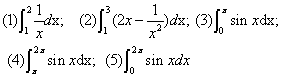
变式1:计算:;
(1)![]() ;(2)
;(2)![]()
解:.(1)
![]()
![]()
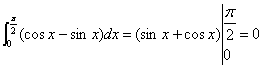
(2)利用导数的几何意义:![]() 与x=0,x=2所围图形是以(0,0)为圆心,2为半径的四分之一个圆,其面积即为
与x=0,x=2所围图形是以(0,0)为圆心,2为半径的四分之一个圆,其面积即为![]() (图略)
(图略)
变式2: 求将抛物线![]() 和直线
和直线![]() 围成的图形绕
围成的图形绕![]() 轴旋转一周得到的几何体的体积.
轴旋转一周得到的几何体的体积.
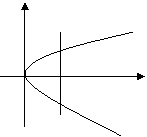 分析:利用定积分的定义解题,应当画出草图.
分析:利用定积分的定义解题,应当画出草图.
解:先求出抛物线![]() 和直线
和直线![]() 交点坐标(1,1),(1,-1)
交点坐标(1,1),(1,-1)
利用定积分的定义易得:
![]()
![]()
![]()
变式3:在曲线![]() 上某一点A处作一切线使之与曲线以及
上某一点A处作一切线使之与曲线以及![]() 轴所围的面积为
轴所围的面积为![]() ,试求:(1)切点A的坐标;(2)在切点A的切线方程.
,试求:(1)切点A的坐标;(2)在切点A的切线方程.