高考数学全国统一模拟考试
数 学(江苏卷)(模拟一)

第I卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,恰有一项是符合题目要求的。
1. 已知集合![]() ,
,![]() ,
,![]() ∩
∩![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 数列![]() (
(![]() )中,
)中,![]() ,且
,且![]() ,则
,则![]()
A.1 B.3 C.5 D.无法确定
3. ![]() 的展开式中常数项等于20,则
的展开式中常数项等于20,则![]() 等于
等于
A.4 B.6 C.8 D.10
4. 空间直线![]() 是成
是成![]() 的异面直线,分别过
的异面直线,分别过![]() 作平面
作平面![]() ,使
,使![]() 也成
也成![]() .这样的平面
.这样的平面![]()
A.有无穷对 B.只有5对 C.只有3对 D. 只有1对
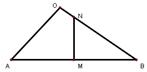 5. 如图
5. 如图![]() ,
,![]() 是边
是边![]() 的垂直平分线,交
的垂直平分线,交![]() 于点N,设
于点N,设![]() ,且
,且![]() ,则
,则![]()
A.![]() B.
B.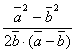
C.![]() D.
D.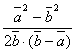
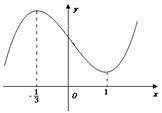 6. 函数
6. 函数![]() 的部分图像如图所示,若方程
的部分图像如图所示,若方程![]() 恰有两个不等根,则有
恰有两个不等根,则有
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D. 以上都不对
D. 以上都不对
7.已知不等式![]() 对于
对于![]() ,
,![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B.![]() C
C![]() . D.
. D.
![]()
8.椭圆![]() 的中心、右焦点、右顶点、右准线与
的中心、右焦点、右顶点、右准线与![]() 轴的交点依次为O、F、A、H,则
轴的交点依次为O、F、A、H,则![]() 的最小值为
的最小值为
A.2 B.3 C. 4 D.不能确定
9.某学校的生物实验室里有一个鱼缸,里面有12条大小差不多的金鱼,8条红色,4条黑色,实验员每次都是随机的从鱼缸中有放回的捞取1条金鱼.若该实验员每周一、二、三3天有课,且每天上、下午各一节,每节课需要捞一条金鱼使用,用过放回.则该实验员在本周有课的这三天中,星期一上、下午所捞到的两条金鱼为同色,且至少有一天捞到不同的颜色金鱼的概率是
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
10.设方程![]() 的两根为
的两根为![]() ,
,![]() (
(![]() <
<![]() ),则
),则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第II卷(非选择题 共100分)
二、填空题:本大题共6小题,每小题5分,共30分。不需要写出解答过程,请把答案直接填空在答题卡相应位置上。
11.垂直于直线x-3y=0且与曲线![]() 相切的直线方程为 ▲ .
相切的直线方程为 ▲ .
12.若x、y满足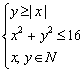 ,则
,则![]() 的最大值为 ▲ .
的最大值为 ▲ .
13.数列{an}中,![]() ,
,![]() ,且
,且![]() ,则常数t= ▲ .
,则常数t= ▲ .
14. 椭圆![]() 的左准线为
的左准线为![]() ,左右焦点分别为
,左右焦点分别为![]() 抛物线
抛物线![]() 的准线为
的准线为![]() ,一个焦点为
,一个焦点为![]() ,
,![]() 与
与![]() 的一个交点为
的一个交点为![]() ,则
,则![]() = ▲ .
= ▲ .
15.![]() 中,
中,![]() 分别是角
分别是角![]() 的对边,已知
的对边,已知![]() ,
,![]() ,现有以下判断:
,现有以下判断:
① ![]() 不可能等于15
不可能等于15
② 若![]() ,则
,则![]()
③ ![]()
④ 若![]() ,则
,则![]() 有两解
有两解
⑤ 作![]() 关于
关于![]() 的对称点
的对称点![]() ,则
,则![]() 的最大值是
的最大值是![]()
⑥ 若![]() 为定点,则动点
为定点,则动点![]() 的轨迹围成的封闭图形的面积是
的轨迹围成的封闭图形的面积是![]() .
.
请将所有正确的判断序号填在横线上 ▲ .
16. 已知函数![]() 且不等式
且不等式![]() 的解集 ▲ .
的解集 ▲ .
三、解答题:本大题共5小题,共70分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分
![]() 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为![]() 、
、![]() 、
、![]() ,已知
,已知![]()
(1)求![]() 的值;
的值;
(2)求![]() 的面积。
的面积。
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
已知![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]() 。
。
(1)当点![]() 在
在![]() 轴上移动时,求
轴上移动时,求![]() 点的轨迹
点的轨迹![]() 的方程;
的方程;
(2)设![]() 为轨迹
为轨迹![]() 上两点,
上两点,![]() ,
,![]() ,
,![]() ,若存在实数
,若存在实数![]() ,使
,使![]() ,且
,且![]() ,求
,求![]() 的值。
的值。
19.(本题满分14分)本题共3个小题,第1小题满分4分,第2小题满分5分,第3小题满分5分
如图,已知正三棱柱![]() 中,
中,![]() ,
,![]() ,三棱锥
,三棱锥![]() 中,
中,
![]() 平面
平面![]() ,且
,且![]() 。
。
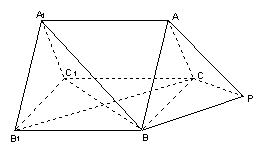 (1)求证:
(1)求证:![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。
20.(本题满分15分)本题共2个小题,第1小题满分7分,第2小题满分8分
已知函数![]() 和
和![]() (其中
(其中![]() ),
),![]() ,
,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)方程![]() 有几个实根?为什么?
有几个实根?为什么?
21.(本题满分15分)本题共2个小题,第1小题满分8分,第2小题满分7分
已知数列{an}满足![]() ,
,![]() ,
,![]() ,
,![]() 为正数 .
为正数 .
(1)若![]() 对
对![]() 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)是否存在![]() ,使得对任意正整数
,使得对任意正整数![]() 都有
都有![]() ?若存在,求出
?若存在,求出![]() 的值;
的值;
若不存在,请说明理由。
高考数学全国统一模拟考试
答题卷(模拟一)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,恰有一项是符合题目要求的。
请将你认为正确的答案填在下面的表格中:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:本大题共6小题,每小题5分,共30分。不需要写出解答过程,请把答案直接填空在答题卡相应位置上。
11、 ;12、 ;
13、 ;14、 ;
15、 ;16、 .
三、解答题:本大题共5小题,共70分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分
解:(1)
(2)
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
解:(1)
(2)
19.(本题满分14分)本题共3个小题,第1小题满分4分,第2小题满分5分,第3小题满分5分
 解:
解:
(1)
(2)
(3)
20.(本题满分15分)本题共2个小题,第1小题满分7分,第2小题满分8分
解:
(1)
(2)
21.(本题满分15分)本题共2个小题,第1小题满分8分,第2小题满分7分
解:
(1)
(2)
高考数学全国统一模拟考试
参考答案与评份标准
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,恰有一项是符合题目要求的。
请将你认为正确的答案填在下面的表格中:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | B | A | B | A | D | C | C | D |
二、填空题:本大题共6小题,每小题5分,共30分。不需要写出解答过程,请把答案直接填空在答题卡相应位置上。
11、![]() 12、7
13、10
12、7
13、10
14、1
15、①②③⑤
16、![]()
三、解答题:本大题共5小题,共70分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
17.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分
解: (1)由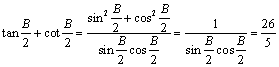 ,得
,得![]() ------------3分
------------3分
![]() 为锐角,
为锐角,![]() , -------5分
, -------5分
![]() --------------------------6分
--------------------------6分
(2)![]()
![]() ---8分
---8分
又![]() ,
,![]() ,得
,得![]() ,
--------------------------10分
,
--------------------------10分
![]() --------------------------12分
--------------------------12分
(若通过![]() 得出
得出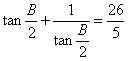 ,求出
,求出![]() ,
,
未舍去![]() ,
,![]() 得两解,扣2分.)
得两解,扣2分.)
18.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分
解: (1)设点![]() ,由
,由![]() 得
得![]() ,
,![]() ,
,
由![]() ,得
,得![]() , ------------------------4分
, ------------------------4分
即![]() .
---------------------6分
.
---------------------6分
(2)由(1)知![]() 为抛物线
为抛物线![]() :
:![]() 的焦点,
的焦点,![]() 为过焦点
为过焦点![]() 的直线与
的直线与![]() 的两个交点.
的两个交点.
①当直线![]() 斜率不存在时,得
斜率不存在时,得![]() ,
,![]() ,
,![]() . ----8分
. ----8分
②当直线斜率存在且不为0时,设![]() ,代入
,代入![]() 得
得
![]() .设
.设![]() ,
,
则![]() ,得
,得![]() , ----12分
, ----12分
(或![]() )
)
![]() ,此时
,此时![]() ,由
,由![]() 得
得
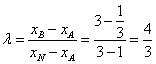 。
---------------14分
。
---------------14分
19.(本题满分14分)本题共3个小题,第1小题满分4分,第2小题满分5分,第3小题满分5分
.解法一:
(1)在![]() 中,
中,![]() ,
,![]() ,
,
∴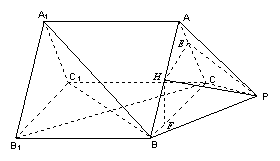
![]() ,取
,取![]() 中点
中点![]() ,
,
![]() ,
, ![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,又
,又![]() 均为锐角,∴
均为锐角,∴![]() , ---------------2分
, ---------------2分
![]() ,又
,又![]() 外,
外, ![]() . ---------------4分
. ---------------4分
(2)∵平面![]()
![]() 平面
平面![]() ,∴
,∴![]() ,过
,过![]() 作
作![]() 于
于![]() ,连结
,连结![]() ,则
,则![]() ,
,
![]() 为二面角
为二面角![]() 的平面角, ------------------------6分
的平面角, ------------------------6分
易知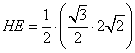 =
=![]() ,∴
,∴![]() ,
,
![]() 二面角
二面角![]() 的大小为
的大小为![]() . ------------------------9分
. ------------------------9分
(其它等价答案给同样的得分)
(3)![]() ,
,![]() 点到平面
点到平面![]() 的距离,就是
的距离,就是![]() 到平面
到平面![]() 的距离,-------------------------------11分
的距离,-------------------------------11分
过![]() 作
作![]() 于
于![]() ,则
,则![]() ,
,![]() 的长度即为所求, 由上
的长度即为所求, 由上![]() (或用等体积
(或用等体积![]() 求)----------------------------------14分
求)----------------------------------14分
解法二:
如图,建立图示空间直角坐标系.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)![]()
(2)利用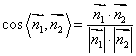 ,其中
,其中![]() 分别为两个半平面的法向量,
分别为两个半平面的法向量,
或利用![]() 求解.
求解.
(3)利用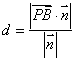 ,其中
,其中![]() 为平面
为平面![]() 的法向量。
的法向量。
20.(本题满分15分)本题共2个小题,第1小题满分7分,第2小题满分8分
解: (1)∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() . 1分
. 1分
![]() ,即
,即![]() ,∴
,∴![]() . 3分
. 3分
①当![]() ,即
,即![]() 时,上式不成立.……………………………4分
时,上式不成立.……………………………4分
②当![]() ,即
,即![]() 时,
时,![]() .由条件
.由条件![]() ,得到
,得到![]() .
.
由![]() ,解得
,解得![]() 或
或![]() . ……………………5分
. ……………………5分
由![]() ,解得
,解得![]() 或
或![]() .…………………………6分
.…………………………6分
![]() m的取值范围是
m的取值范围是![]() 或
或![]() . ………………………7分
. ………………………7分
(2)有一个实根.…………………………………………………………9分
![]() ,即
,即![]() .
.
记![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,![]()
![]() . ………………………10分
. ………………………10分
![]() △>0,故
△>0,故![]() 有相异两实根
有相异两实根![]() .
.
![]() ,∴
,∴ 显然
显然![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() . …………12分
. …………12分
于是![]()
![]()
![]()
![]()
![]()
![]() .
.
而![]() 为三次函数
为三次函数![]() 的极小值点,故
的极小值点,故![]() 与x轴只有一个交点.
与x轴只有一个交点.
∴ 方程![]() 只有一个实根.…………………………15分
只有一个实根.…………………………15分
21.(本题满分15分)本题共2个小题,第1小题满分8分,第2小题满分7分
解: (1)∵![]() 为正数,
为正数,![]() ①,
①,![]() =1,∴
=1,∴![]() >0(n∈N*),……… 1分
>0(n∈N*),……… 1分
又![]() ②,①—②两式相减得
②,①—②两式相减得![]() ,
,
∴![]() 与
与![]() 同号,
---------------------4分
同号,
---------------------4分
∴![]() 对n∈N*恒成立的充要条件是
对n∈N*恒成立的充要条件是![]() >0.
---------------------7分
>0.
---------------------7分
由![]() =
=![]() >0,得
>0,得![]() >7 . ---------------------8分
>7 . ---------------------8分
(2)证法1:假设存在![]() ,使得对任意正整数
,使得对任意正整数![]() 都有
都有![]() .
.
则![]() ,则
,则![]() >17 .
--------------------9分
>17 .
--------------------9分
另一方面,![]() =
=![]() =
=![]()
![]() ,---------11分
,---------11分
∴![]()
![]() ,
,![]()
![]() ,……,
,……,![]()
![]() ,
,
∴![]()
![]() ,∴
,∴![]()
![]() =
=![]() , ①
, ①
--------------------------------14分
当m>16时,由①知,![]() ,不可能使
,不可能使![]() 对任意正整数n恒成立,
对任意正整数n恒成立,
--------------------------------15分
∴m≤16,这与![]() >17矛盾,故不存在m,使得对任意正整数n都有
>17矛盾,故不存在m,使得对任意正整数n都有![]() .
.
--------------------------------16分
(2)证法2:假设存在m,使得对任意正整数n都有![]() .
.
则![]() ,则
,则![]() >17 .
--------------------9分
>17 .
--------------------9分
另一方面,![]() ,
------------------11分
,
------------------11分
∴![]() ,
,![]() ,……,
,……,![]() ,
,
∴![]() ,
,![]() ①
-----------------14分
①
-----------------14分
当m>16时,由①知,![]() ,不可能使
,不可能使![]() 对任意正整数恒成立, --15分
对任意正整数恒成立, --15分
∴m≤16,这与![]() >17矛盾,故不存在m,使得对任意正整数n都有
>17矛盾,故不存在m,使得对任意正整数n都有![]() 。 ---16分
。 ---16分