高考数学全真模拟冲刺试卷
第Ⅰ卷(选择题共60分)
一、选择题:本大题共12小题,每小题5分,共60分.
1.已知集合![]() ,若
,若![]() ,则
,则![]() 等于 ( )
等于 ( )
A. 1 B. 2 C. 1或2 D 8
2.若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,那么函数解析式为![]() ,值域为
,值域为![]() 的“同族函数”共有 ( )
的“同族函数”共有 ( )
A.7个 B.8个 C.9个 D.10个
3.数列![]() 中,
中,![]() ,
,![]() ,且数列
,且数列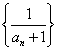 是等差数列,则
是等差数列,则![]() 等于 ( )
A.
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
4.把函数![]() 的图象沿向量
的图象沿向量![]() 的方向平移后,所得的图象关于y轴对称,则m的最小值是
(
)
的方向平移后,所得的图象关于y轴对称,则m的最小值是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、O是平面上一定点,A、B、C是平面上不共线的三个点,动点P满点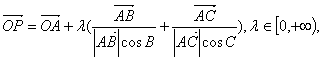 ,则P点的轨迹一定通过
,则P点的轨迹一定通过![]() 的
的
A.重心 B.垂心 C.内心 D.外心 ( )
6.过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于A、B两点,如果
交于A、B两点,如果![]() ,则 ( )
,则 ( )
A.![]() 的方程为
的方程为![]() ;
;
B.![]() 的方程为
的方程为![]() ;
;
C.![]() 的方程为
的方程为![]() ;
;
D.![]() 的方程为
的方程为![]() ;
;
7.F1、F2是双曲线![]() 的焦点,点P在双曲线上,若点P到焦点F1的距离等于9,则点P到焦点F2的距离为
( )
的焦点,点P在双曲线上,若点P到焦点F1的距离等于9,则点P到焦点F2的距离为
( )
A.1 B.17 C.1或17 D.6
8.已知复数![]() =a+i,z2=1+a 2 i,若
=a+i,z2=1+a 2 i,若![]() 是实数,则实数a的值等于
( )
是实数,则实数a的值等于
( )
A.1 B.-1 C.-2 D.2
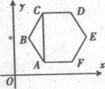 9.如图正六边形ABCDEF中,AC∥y轴.从六个顶点中任取三点,使这三点能确定一条形如y=ax 2+bx+c (a≠0)的抛物线的概率是 ( )
9.如图正六边形ABCDEF中,AC∥y轴.从六个顶点中任取三点,使这三点能确定一条形如y=ax 2+bx+c (a≠0)的抛物线的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.条件中能使命题“a//b且b//c![]() a//c”为真命题的条件的个数是 ( )
a//c”为真命题的条件的个数是 ( )
① a,b,c都表示直线; ② a,b,c中有两个表示直线,另一个表示平面;
③ a,b,c都表示平面; ④ a,b,c中有两个表示平面,另一个表示直线;
A. 1个 B.2个 C.3个 D.4个
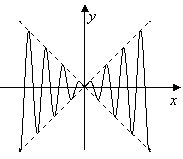 11.如图,虚线部分是四个象限的角平分线,实线部分是函数
11.如图,虚线部分是四个象限的角平分线,实线部分是函数
![]() 的部分图像,则
的部分图像,则![]() 可能是
( )
可能是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.一机器猫每秒钟前进或后退一步,程序设计师让机器猫以前进3步,然后再后退2步的规律移动。如果将此机器猫放在数轴的原点,面向正方向,以1步的距离为1单位长移动。令P(n)表示第n秒时机器猫所在位置的坐标,且P(0)=0,则下列结论中错误的是 ( )
A.P(3)=3 B.P(5)=1 C.P(101)=21 D.P(101)> P(104)
第Ⅱ卷(非选择题共120分)
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上.
13.在平面直角坐标系中,x轴的正半轴上有2006个点,y轴的正半轴上有2007个点,这4013个点任意两点连线,则所有连线段的交点落入第一象限的最多有______个.(用式子作答)
14.若不等式![]() 的解集为
的解集为![]() ,则实数的取值范围是______________
,则实数的取值范围是______________
15.若![]() ,则
,则
![]() ______(用数字作答).
______(用数字作答).
16.对于直角坐标平面内的任意两点![]() ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”:![]() 。给出下列三个命题:①若点C在线段AB上,则
。给出下列三个命题:①若点C在线段AB上,则![]() ②在△ABC中,若∠C=900,则
②在△ABC中,若∠C=900,则![]() ③在△ABC中
③在△ABC中![]() 。其中真命题的是______________
。其中真命题的是______________
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
17.(本题12分)在△ABC中,已知角A,B,C所对的三条边分别是a,b,c,且满足b2 = ac.
(1)求角B取值范围; (2)求函数![]() 的取值范围.
的取值范围.
18.(本题12分)小张有一只放有a个红球,b个黄球,c个白球的箱子,且a+b+c =6 (a,b,c![]() N),小刘有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
N),小刘有一只放有3个红球,2个黄球,1个白球的箱子,两人各自从自己的箱子中任取一球,规定:当两球同色时小张胜,异色时小刘胜.
(1) 用a、b、c表示小张胜的概率;
(2) 若又规定当小张取红、黄、白球而胜的得分分别为1分、2分、3分,否则得0分,求小张得分的期望的最大值及此时a、b、c的值.
19.(本题12分)设函数![]() 其中
其中![]() .
.
(1)
若![]() ,且函数
,且函数![]() 的最大值为2,最小值为
的最大值为2,最小值为![]() ,求
,求![]() 的解析式;
的解析式;
(2)在(1)的条件下设函数![]() 在
在![]() 上的值域是
上的值域是![]() ,试求
,试求![]() 的取值范围.
的取值范围.
20.(本题12分)直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为a的菱形,且![]() ,侧棱AA1长等于3a,O为底面ABCD对角线的交点.
,侧棱AA1长等于3a,O为底面ABCD对角线的交点.
(1)求证:OA1∥平面B1CD1;
(2)求异面直线AC与A1B所成的角;
(3)在棱![]() 上取一点F,问AF为何值时,C1F⊥平面BDF?
上取一点F,问AF为何值时,C1F⊥平面BDF?
21.(本题12分)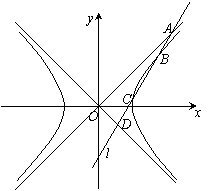 已知双曲线M:x2-y2=1,直线l与双曲线M的实轴不垂直,且依次交直线y=x、双曲线M、直线y=-x于A、B、C、D 四点,O为坐标原点.
已知双曲线M:x2-y2=1,直线l与双曲线M的实轴不垂直,且依次交直线y=x、双曲线M、直线y=-x于A、B、C、D 四点,O为坐标原点.
(1) 若![]() ,求△AOD的面积;
,求△AOD的面积;
(2) 若△BOC的面积等于△AOD面积的![]() ,求证:
,求证: ![]() .
.
22.(本题14分)已知数列![]() 满足
满足![]() >0,且对一切n∈N+ ,有ni=1=,其中Sn=ni=1ai,
>0,且对一切n∈N+ ,有ni=1=,其中Sn=ni=1ai,
(1) 求证:对一切n∈N+,有-an+1=2Sn;
(2) 求数列![]() 的通项公式;
的通项公式;
(3) 求证:nk=1<3.
数学答案
一、选择题
1、答案C。由集合N中的不等式得0<x<3,又由于![]() ,故
,故![]() ,所以a=1或2
,所以a=1或2
2、答案C。
分别令x2=1和4得x=![]() 。要使得值域为
。要使得值域为![]() ,定义域必含
,定义域必含![]() 中的至少一个和
中的至少一个和![]() 中的至少一个。所以组合起来有如下9种:
中的至少一个。所以组合起来有如下9种:![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
3、答案B。数列![]() 的公差为
的公差为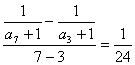 ,所以
,所以![]() =
=![]() ,因此
,因此![]() =
=![]()
4、答案C。![]() =
=![]() ,按a平移得
,按a平移得![]() ,令
,令![]() =
=![]() ,得
,得![]() ,当k=1时m取得最小正值
,当k=1时m取得最小正值![]() 。
。
5、答案B。由结构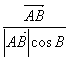 想到向量的数量积,原式即为
想到向量的数量积,原式即为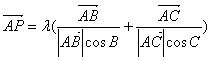 ,等式两边同时点乘
,等式两边同时点乘![]() ,得
,得![]() ,所以P过
,所以P过![]() 的垂心。
的垂心。
6、答案A。由![]() 得圆心到直线
得圆心到直线![]() 的距离为3,再由点到直线的距离公式得直线
的距离为3,再由点到直线的距离公式得直线![]() 的斜率是
的斜率是![]() ,得到一个解,说明可能存在的另一条直线的斜率不存在,故去验证得A答案。
,得到一个解,说明可能存在的另一条直线的斜率不存在,故去验证得A答案。
7、答案D。由于双曲线中a+c=4+6=10>9,所以点P只能在靠近焦点F1的那一支上,故![]()
8、答案B
。 ![]() ,故a 3+1=0,得a =-1.
,故a 3+1=0,得a =-1.
9、答案 C。 由二次函数的性质知三点可确定一条抛物线,但两点连线不能与纵轴平行,
故其概率为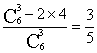
10、答案B。①由公理4可得,③是两平面平行的判定定理,②和④可通过一一验证来否定。
11、答案A。由图知此函数是偶函数,故排除B与D,又函数图象落在![]() 区域内,所以选A。
区域内,所以选A。
12、答案D。由于“机器猫以前进3步,然后再后退2步的规律移动”,因此可以认为机器猫的运动以5为周期向前前进1步。易推A与B成立,101除以5得20余1,所以P(101)=21,而104除以5得20余4,故P(104)=22 > P(101)
二、填空题:
13、答案为![]() 。 构造凸四边形,凸四边形对角线的交点在凸四边形内,故最多有
。 构造凸四边形,凸四边形对角线的交点在凸四边形内,故最多有![]() 个点。
个点。
14、答案为![]() 。令
。令![]() ,它表示以(2,0)为圆心、2为半径的上半个圆;令
,它表示以(2,0)为圆心、2为半径的上半个圆;令![]() ,它表示一条过原点的直线。现要使得
,它表示一条过原点的直线。现要使得![]() 在0<x≤4成立,即在0<x≤4时直线落在半圆下方,故斜率
在0<x≤4成立,即在0<x≤4时直线落在半圆下方,故斜率![]() 。
。
15、答案为0。 两边求导,再分别把x赋值x=2,x=0,最后把所得两式相乘即得.
16、答案为①。设![]() ,利用定义知①成立;②③验证可以先这样建系:以C为原点,CA为x轴的正向建系,则
,利用定义知①成立;②③验证可以先这样建系:以C为原点,CA为x轴的正向建系,则![]() ,故②不成立,③不成立。
,故②不成立,③不成立。
三、解答题:
17.(1)由b2=ac和由余弦定理,得
![]() ……………………………2分
……………………………2分
≥![]() . ……………………………4分
. ……………………………4分
又∵B∈(0,π), ∴ 0<B≤![]() . ……………………………6分
. ……………………………6分
(2)![]() =
=![]()
=![]() , ……………………………8分
, ……………………………8分
又 0<B≤![]() ,∴
,∴![]() <B+
<B+![]() ≤
≤![]() .……………………………10分
.……………………………10分
∴ ![]() ,即原函数的值域是(1,
,即原函数的值域是(1,![]() ).………………12分
).………………12分
18、解:(1)P(小张胜)=P(两人均取红球)+P(两人均取黄球)+P(两人均取白球)
=![]() +
+ ![]() +
+ ![]() =
=![]() ……………………………5分
……………………………5分
(2)
设小张的得分为随机变量![]() ,则
,则
P(![]() =3)=
=3)= ![]() ,P(
,P(![]() =2)=
=2)= ![]() ,P(
,P(![]() =1)=
=1)= ![]() ,
,
P(![]() =0)=1一P(小张胜)=1一
=0)=1一P(小张胜)=1一![]() ,……………………………9分
,……………………………9分
∴E![]() =3×
=3×![]() +2×
+2×![]() +1×
+1×![]() +0×(1一
+0×(1一![]() )
)
= ![]()
∵ a,b,c∈N,a+b+c=6,∴b=6,此时a=c=0,
∴当b=6时,E![]() =
= ![]() ,此时a=c=0,b=6…………………12分
,此时a=c=0,b=6…………………12分
19.解:(1)因为 ![]()
又 ![]() ,所以
,所以 ![]() 因为
因为 ![]() ,…………………2分
,…………………2分
所以 当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
…………………4分
;
…………………4分
解得:![]()
所以 ![]() ;
…………………6分
;
…………………6分
(2)
因为![]()
又![]() …………………8分
…………………8分
因为 当![]()
![]() 时,值域为
时,值域为![]() .
.
所以 ![]() 或
或![]() , …………………10分
, …………………10分
所以 ![]() ,
,
所以 ![]() . …………………12分
. …………………12分
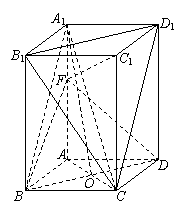
20.(方法一)(1) 连A1C1,设其与B1D1交于点O1.
∵A1O1![]() OC, ∴四边形A1O1OC为平行四边形,
OC, ∴四边形A1O1OC为平行四边形,
∴OA1//O1C, ![]() 平面B1CD1,
平面B1CD1, ![]() 平面B1CD1,
平面B1CD1,
∴OA1∥平面B1CD1.…………………………3分
(2) ∵A1C1//AC,∴![]() 就是异面直线AC与A1B所成的角或其补角.
就是异面直线AC与A1B所成的角或其补角.
由题意得![]()
根据余弦定理得 ![]() ……………………6分
……………………6分
故异面直线AC与A1B所成的角为![]() …………………………………7分
…………………………………7分
(3) ∵ABCD是菱形,∴![]() 又
又![]() ∴
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ……………………………………………9分
……………………………………………9分
故C1F⊥平面BOF ![]()
![]() ∴
∴![]() .……………10分
.……………10分
设![]() ,则
,则![]() ∴
∴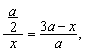 即
即![]()
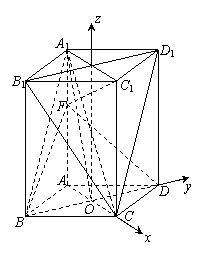 解得
解得![]()
故当AF![]() 时,C1F⊥平面BOF.………………………12分
时,C1F⊥平面BOF.………………………12分
(方法二) 以O为原点,OC、OD所在直线分别为
x轴、y轴,则O(0, 0, 0), ![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .……………3分
.……………3分
(1) ![]()
![]()
∴![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴OA1∥平面B1CD1.……………………………………………………………………5分
(2)![]() ,
,
![]() ,
,
于是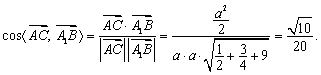
故异面直线AC与A1B所成的角为![]() ……………………………………8分
……………………………………8分
(3) 设![]() 为
为![]() 上任意一点,则
上任意一点,则![]() .
.
∵![]() ,于是C1F⊥平面BOF
,于是C1F⊥平面BOF![]()
![]()
解得![]() . 即
. 即![]() 时,C1F⊥平面BOF.………………………12分
时,C1F⊥平面BOF.………………………12分
21.(1)设![]()
得![]() …………………………………………2分
…………………………………………2分
显然![]() ,
,
即![]() .
.
设![]()
![]() ………………………………………………4分
………………………………………………4分
设![]()
由![]() 。
。
![]() , 所以
, 所以![]() 。………………………………6分
。………………………………6分
所以 ![]() , 整理,得
, 整理,得 ![]() .
.
![]() ,
, ![]()
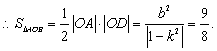 …………………………………………………8分
…………………………………………………8分
(2)设![]()
![]()
![]() ,
,
![]() ……………………………………10分
……………………………………10分
![]() ,
, ![]() ,
, ![]() .
.
又![]() ,
, ![]() …12分
…12分
22. (1) 由ni=1![]() =Sn2, (1)
=Sn2, (1)
得n+1i=1![]() =Sn+12, (2)
…………………2分
=Sn+12, (2)
…………………2分
(2)-(1),得![]() =(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1)
an+1.
=(Sn+1+Sn)(Sn+1-Sn)=(2 Sn+an+1)
an+1.
∵ an+1 >0,∴an+12-![]() =2Sn. …………………4分
=2Sn. …………………4分
(2)由an+12-![]() =2Sn,及an2-an =2Sn-1 (n≥2),
=2Sn,及an2-an =2Sn-1 (n≥2),
两式相减,得(an+1+ an)( an+1-an)= an+1+ an.
∵an+1+ an >0,∴an+1-an =1(n≥2) …………………6分
当n=1,2时,易得a1=1,a2=2,∴an+1 - an =1(n≥1).…………………8分
∴{ an}成等差数列,首项a1=1,公差d=1,故an=n . …………………9分
(3)nk=1![]() =nk=1
=nk=1![]() <1+nk=2
<1+nk=2
<1+nk=2=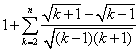
=1+ nk=2(- ) =1+1+![]() -
-![]() - <2+
- <2+![]() <3.
<3.
…………………14分