高考数学函数复习练习
今天,我怕谁之三
1.(1)设![]() 是集合
是集合![]() 到
到![]() 的映射,下列说法正确的是
的映射,下列说法正确的是
A、![]() 中每一个元素在
中每一个元素在![]() 中必有象 B、
中必有象 B、![]() 中每一个元素在
中每一个元素在![]() 中必有原象
中必有原象
C、![]() 中每一个元素在
中每一个元素在![]() 中的原象是唯一的 D、
中的原象是唯一的 D、![]() 是
是![]() 中所在元素的象的集合
中所在元素的象的集合
(2)点![]() 在映射
在映射![]() 的作用下的象是
的作用下的象是![]() ,则在
,则在![]() 作用下点
作用下点![]() 的原象为点________
的原象为点________
(3)设集合![]() ,映射
,映射![]() 满足条件“对任意的
满足条件“对任意的![]() ,
,![]() 是奇数”,这样的映射
是奇数”,这样的映射![]() 有____个;
有____个;
2.(1)已知函数![]() ,
,![]() ,那么集合
,那么集合![]() 中所含元素的个数有 个;
中所含元素的个数有 个;
(2)若函数![]() 的定义域、值域都是闭区间
的定义域、值域都是闭区间![]() ,则
,则![]() =
=
(3)函数![]() 定义域是[
定义域是[![]() ]
]![]() ,则函数的值域中共有
个整数。
,则函数的值域中共有
个整数。
3.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“文峰函数”,那么解析式为![]() ,值域为{4,1}的“文峰函数”共有______个
,值域为{4,1}的“文峰函数”共有______个
4.(1)函数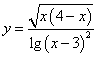 的定义域是__
_
的定义域是__
_
(2)函数![]() 的定义域是 A.
的定义域是 A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(3)设![]() ,则
,则![]() 的定义域为 ( )
的定义域为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(4)若函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 的定义域为________
的定义域为________
(5)已知函数f(x)的定义域为(0,1),求f(x-2)的定义域.
(6)已知函数f(2x+1)的定义域为(0,1),求f(x)的定义域.
(7)已知![]() 的图象过点(2,1),则
的图象过点(2,1),则![]() 的值域为_____
的值域为_____
5(1)![]() 的值域为_____(2)
的值域为_____(2)![]() 的值域为____
的值域为____
(3)![]() 的值域为_____(4)求函数
的值域为_____(4)求函数![]() 的值域
.
的值域
.
(5)求函数![]() 的值域
。(6)求函数
的值域
。(6)求函数![]() 的值域
。
的值域
。
(7)求函数y=![]() 的值域
。(8)求函数y=
的值域
。(8)求函数y=![]() 的值域
。(9)求函数
的值域
。(9)求函数![]() 的值域
。(10)求函数
的值域
。(10)求函数![]() 的值域
。
的值域
。
(11)求函数![]() 的值域
。(12)求函数y=x-
的值域
。(12)求函数y=x-![]() 的值域
。
的值域
。
(13)求函数![]() 的值域
(14)求函数
的值域
(14)求函数![]() 的值域
的值域
(15)求函数![]() ,
,![]() 的最小值 。
的最小值 。
友情提示
1.映射![]() : A
: A![]() B的概念。在理解映射概念时要注意:
B的概念。在理解映射概念时要注意:
⑴A中元素必须都有象且唯一;⑵B中元素不一定都有原象,但原象不一定唯一。
2.函数![]() : A
: A![]() B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与
B是特殊的映射。特殊在定义域A和值域B都是非空数集!据此可知函数图像与![]() 轴的垂线至多有一个公共点,但与
轴的垂线至多有一个公共点,但与![]() 轴垂线的公共点可能没有,也可能有任意个。
轴垂线的公共点可能没有,也可能有任意个。
3. 同一函数的概念。构成函数的三要素是定义域,值域和对应法则。而值域可由定义域和对应法则唯一确定,因此当两个函数的定义域和对应法则相同时,它们一定为同一函数。
4. 求函数定义域的常用方法(在研究函数问题时要树立定义域优先的原则):
(1)根据解析式要求如偶次根式的被开方大于零,分母不能为零,对数![]() 中
中![]() 且
且![]() ,三角形中
,三角形中![]() , 最大角
, 最大角![]() ,最小角
,最小角![]() 等。(2)根据实际问题的要求确定自变量的范围。
等。(2)根据实际问题的要求确定自变量的范围。
(3)复合函数的定义域:若已知![]() 的定义域为
的定义域为![]() ,其复合函数
,其复合函数![]() 的定义域由不等式
的定义域由不等式![]() 解出即可;若已知
解出即可;若已知![]() 的定义域为
的定义域为![]() ,求
,求![]() 的定义域,相当于当
的定义域,相当于当![]() 时,求
时,求![]() 的值域(即
的值域(即![]() 的定义域)。
的定义域)。
5.求函数值域(最值)的方法:
(1)配方法――二次函数(二次函数在给出区间上的最值有两类:一是求闭区间![]() 上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),
上的最值;二是求区间定(动),对称轴动(定)的最值问题。求二次函数的最值问题,勿忘数形结合,注意“两看”:一看开口方向;二看对称轴与所给区间的相对位置关系),
(2)换元法――通过换元把一个较复杂的函数变为简单易求值域的函数,其函数特征是函数解析式含有根式或三角函数公式模型,
(3)函数有界性法――直接求函数的值域困难时,可以利用已学过函数的有界性,来确定所求函数的值域,最常用的就是三角函数的有界性,
(4)单调性法――利用一次函数,反比例函数,指数函数,对数函数等函数的单调性,
(5)数形结合法――函数解析式具有明显的某种几何意义,如两点的距离、直线斜率、等等,
注意:求两点距离之和时,要将函数式变形,使两定点在![]() 轴的两侧,而求两点距离之差时,则要使两定点在
轴的两侧,而求两点距离之差时,则要使两定点在![]() 轴的同侧。
轴的同侧。
(6)判别式法――对分式函数(分子或分母中有一个是二次)都可通用,但这类题型有时也可以用其它方法进行求解,不必拘泥在判别式法上,也可先通过部分分式后,再利用均值不等式:
①![]() 型,可直接用不等式性质,②
型,可直接用不等式性质,②![]() 型,先化简,再用均值不等式,③
型,先化简,再用均值不等式,③![]() 型,通常用判别式法;④
型,通常用判别式法;④![]() 型,可用判别式法或均值不等式法,
型,可用判别式法或均值不等式法,
(7)不等式法――利用基本不等式![]() 求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
求函数的最值,其题型特征解析式是和式时要求积为定值,解析式是积时要求和为定值,不过有时须要用到拆项、添项和两边平方等技巧。
(8)导数法――一般适用于高次多项式函数
提醒:(1)求函数的定义域、值域时,你按要求写成集合形式了吗?
(2)函数的最值与值域之间有何关系?
1.(1)A;(2)(2,-1);(3)12;2.(1)0或1;(2)2(3).![]() 个3. 9;4.(1)
个3. 9;4.(1)![]() ;
;
(2)B.(3)(B)(4) [1,5](5){x|2<x<3};(6){x|1<x<3}(7) [2, 5]5(1)![]() (2)
(2)![]()
(3)(0,1);(4)![]() .(5)
.(5)![]() 。(6)
。(6)![]() 。(7){y y>1 或y
。(7){y y>1 或y![]()
![]() 且y
且y![]() R}.
R}.
(8)![]() (9)
(9)![]() .(10)
.(10)![]() (11)
(11)![]() 。(12){y y
。(12){y y![]() 1且y
1且y![]() R}.(13)
R}.(13)![]() .(14)
.(14)![]() 。
。
(15)(答:-48)
函数基本概念回归课本复习材料2
今天,我怕谁之四
6.(1)设函数![]() ,则使得
,则使得![]() 的自变量
的自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)已知![]() ,则不等式
,则不等式![]() 的解集是________
的解集是________
(3)已知函数![]() ,满足
,满足![]() ,当
,当![]()
![]() 。求函数
。求函数![]() 在
在![]() 上的解析式
上的解析式
(4)函数![]() 是偶函数,
是偶函数,![]()
![]() 。求
。求![]()
![]() 得表达式
。
得表达式
。
(5)已知奇函数![]() ,当
,当![]()
![]() 。求函数
。求函数![]() 的解析式
的解析式
7.1)已知二次函数![]() 的对称轴为
的对称轴为![]() ,截
,截![]() 轴上的弦长为
轴上的弦长为![]() ,且过点
,且过点![]() ,求函数的解析式
.
,求函数的解析式
.
(2)已知二次函数![]() 的二次项系数为
的二次项系数为![]() ,且方程
,且方程![]() 的解分别是-1,3,若方程
的解分别是-1,3,若方程![]() 有两个相等的实数根,求
有两个相等的实数根,求![]() 的解析式
的解析式
(3)已知![]() 求
求![]() 的解析式
;
的解析式
;
(4)已知![]() ,求
,求![]() (5)已知
(5)已知![]() ,求
,求![]()
(5)已知![]() ,求
,求![]() 的解析式
;
的解析式
;
(6)已知![]() 是奇函数,
是奇函数,![]() 是偶函数,且
是偶函数,且![]() +
+![]() =
=![]() ,则
,则![]() = __。
= __。
8. (1)函数![]() 在区间[1, 2]上存在反函数的充要条件是
在区间[1, 2]上存在反函数的充要条件是
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
![]()
![]()
(2)函数![]() 的反函数不是
的反函数不是![]() ,而是
。
,而是
。
(3)设![]() .求
.求![]() 的反函数
的反函数![]()
(4)已知函数![]() 的图象过点(1,1),那么
的图象过点(1,1),那么![]() 的反函数的图象一定经过点____
的反函数的图象一定经过点____
(5)已知函数![]() ,若函数
,若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,求
对称,求![]() 的值
的值
(6)已知函数![]() ,则方程
,则方程![]() 的解
的解![]() ______;
______;
(7)设函数f(x)的图象关于点(1,2)对称,且存在反函数![]() ,f (4)=0,则
,f (4)=0,则![]() =
=
(8)已知函数![]() 的图象
的图象
过(1,2),则函数![]() 的图象一定经过
的图象一定经过
9.(1)函数![]() 是奇函数,定义域是
是奇函数,定义域是![]() ,则
,则![]()
(2)判断函数![]() 的奇偶性____(3)判断
的奇偶性____(3)判断![]() 的奇偶性___.
的奇偶性___.
(4)若定义在R上的偶函数![]() 在
在![]() 上是减函数,且
上是减函数,且![]() =2,则不等式
=2,则不等式![]() 的解集为
的解集为
(5) 判断下列函数![]() 的奇偶性
(6)判断下列函数
的奇偶性
(6)判断下列函数![]() 奇偶性
奇偶性
(7) 判断下列各函数f(x)=![]() 的奇偶性: (8)若
的奇偶性: (8)若![]() 为奇函数,则实数
为奇函数,则实数![]() =
=
(9)若将函数![]() ,表示成一个奇函数
,表示成一个奇函数![]() 和一个偶函数
和一个偶函数![]() 之和,则
之和,则![]() =____
=____
友 情 提 示 6.分段函数的概念。分段函数是在其定义域的不同子集上,分别用几个不同的式子来表示对应关系的函数,它是一类较特殊的函数。在求分段函数的值![]() 时,一定首先要判断
时,一定首先要判断![]() 属于定义域的哪个子集,然后再代相应的关系式;分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。
属于定义域的哪个子集,然后再代相应的关系式;分段函数的值域应是其定义域内不同子集上各关系式的取值范围的并集。
7.求函数解析式的常用方法:
(1)待定系数法――已知所求函数的类型(二次函数的表达形式有三种:一般式:![]() ;顶点式:
;顶点式:![]() ;零点式:
;零点式:![]() ,要会根据已知条件的特点,灵活地选用二次函数的表达形式)。
,要会根据已知条件的特点,灵活地选用二次函数的表达形式)。
(2)代换(配凑)法――已知形如![]() 的表达式,求
的表达式,求![]() 的表达式。这里需值得注意的是所求解析式的定义域的等价性,即
的表达式。这里需值得注意的是所求解析式的定义域的等价性,即![]() 的定义域应是
的定义域应是![]() 的值域。
的值域。
(3)方程的思想――已知条件是含有![]() 及另外一个函数的等式,可抓住等式的特征对等式的进行赋值,从而得到关于
及另外一个函数的等式,可抓住等式的特征对等式的进行赋值,从而得到关于![]() 及另外一个函数的方程组。
及另外一个函数的方程组。
8. 反函数:(1)存在反函数的条件是对于原来函数值域中的任一个![]() 值,都有唯一
值,都有唯一![]() 值与之对应,单调函数一定存在反函数,但反之不成立;偶函数只有
值与之对应,单调函数一定存在反函数,但反之不成立;偶函数只有![]() 有反函数;周期函数一定不存在反函数。
有反函数;周期函数一定不存在反函数。
(2)求反函数的步骤:①反求![]() ;②互换
;②互换 ![]() 、
、![]() ;③注明反函数的定义域(原来函数的值域)。注意函数
;③注明反函数的定义域(原来函数的值域)。注意函数![]() 的反函数不是
的反函数不是![]() ,而是
,而是![]() 。
。
(3)反函数的性质:①反函数的定义域是原来函数的值域,反函数的值域是原来函数的定义域。②![]() 的图象与其反函数
的图象与其反函数![]() 的图象关于直线
的图象关于直线![]() 对称,注意函数
对称,注意函数![]() 的图象与
的图象与![]() 的图象相同。③
的图象相同。③![]() 。④互为反函数的两个函数具有相同的单调性和奇函数性。
。④互为反函数的两个函数具有相同的单调性和奇函数性。
9.函数的奇偶性。
(1)具有奇偶性的函数的定义域的特征:定义域必须关于原点对称!为此确定函数的奇偶性时,务必先判定函数定义域是否关于原点对称。
(2)确定函数奇偶性的常用方法(若所给函数的解析式较为复杂,应先化简,再判断其奇偶性):
①定义法:②利用函数奇偶性定义的等价形式:![]() 或
或![]() (
(![]() )。③图像法:奇函数的图象关于原点对称;偶函数的图象关于
)。③图像法:奇函数的图象关于原点对称;偶函数的图象关于![]() 轴对称。
轴对称。
(3)函数奇偶性的性质:
①奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性恰恰相反.
②如果奇函数有反函数,那么其反函数一定还是奇函数.
③若![]() 为偶函数,则
为偶函数,则![]() .
.
④奇函数![]() 定义域中含有0,则必有
定义域中含有0,则必有![]() .故
.故![]() 是
是![]() 为奇函数的既不充分也不必要条件。
为奇函数的既不充分也不必要条件。
⑤定义在关于原点对称区间上的任意一个函数,都可表示成“一个奇函数与一个偶函数的和(或差)”。
⑥复合函数的奇偶性特点是:“内偶则偶,内奇同外”.⑦既奇又偶函数有无穷多个(![]() ,定义域是关于原点对称的任意一个数集).6.(1)
,定义域是关于原点对称的任意一个数集).6.(1)![]() );(2)
);(2)![]() )(3)
)(3)![]()
![]() ,
,![]() 。(4)
。(4)![]() 。(5)
。(5)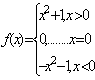 7. (1)
7. (1)![]() .(2)
.(2)![]() 或
或![]() . (3)
. (3)![]() ;(4)
;(4)![]() (
(![]() 或
或![]() ).(5).
).(5).![]() .(6)
.(6)![]() ;(7)
;(7)![]() 。8. (1)D;(2)
。8. (1)D;(2)![]() 。(3)
。(3)![]() (4):(1,3);(5)
(4):(1,3);(5)![]() ; (6)1;(7)-2;(8)(1,2)。9.(1)
; (6)1;(7)-2;(8)(1,2)。9.(1)![]() (2)奇。(3)偶(4)
(2)奇。(3)偶(4)![]() )(5) 非奇非偶.(6)偶。(7)奇(8) 1.(9)
)(5) 非奇非偶.(6)偶。(7)奇(8) 1.(9) ![]() =
=![]()
函数基本概念回归课本复习材料3
今天,我怕谁之五
10.(1)已知函数![]() 在区间
在区间![]() 上是增函数,则
上是增函数,则![]() 的取值范围是____;
的取值范围是____;
(2)若函数![]() 在区间(-∞,4] 上是减函数,那么实数
在区间(-∞,4] 上是减函数,那么实数![]() 的取值范围是____;
的取值范围是____;
(3)已知函数![]() 在区间
在区间![]() 上为增函数,则实数
上为增函数,则实数![]() 的取值范围_____;
的取值范围_____;
(4)函数![]() 的单调递增区间是________。
的单调递增区间是________。
(5)若函数![]() 在区间
在区间![]() 上为减函数,求
上为减函数,求![]() 的取值范围
;
的取值范围
;
(6)函数![]() 在
在![]() 上是增函数,求
上是增函数,求![]() 的取值范围
.
的取值范围
.
(7)已知函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() 的取值范围是
.
的取值范围是
.
(8)已知奇函数![]() 是定义在
是定义在![]() 上的减函数,若
上的减函数,若![]() ,求实数
,求实数![]() 的取值范围
的取值范围
(9)函数![]() 在
在![]() 上增函数,图像过
上增函数,图像过![]() ,则不等式
,则不等式![]() 的解集
。
的解集
。
(10)下列函数既是奇函数,又在区间![]() 上单调递减的是( )
上单调递减的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(11)若函数f(x)=![]() , 则该函数在(-∞,+∞)上是
( )
, 则该函数在(-∞,+∞)上是
( )
(A)单调递减无最小值 (B) 单调递减有最小值 (C)单调递增无最大值 (D) 单调递增有最大值
11.(1)若函数![]() 是偶函数,则函数
是偶函数,则函数![]() 的对称轴方程是______.
的对称轴方程是______.
(2)直线![]() 是函数
是函数![]() 的图象的一条对称轴,那么
的图象的一条对称轴,那么![]() 的图象关于
的图象关于![]() 对称
对称
(3)函数![]() 的图象与
的图象与![]() 轴的交点个数有____个
轴的交点个数有____个
(4)若0<a<1,b<-1,则函数f(x)=ax+b的图象不经过( )
A.第一象限 B.第二象限C.第三象限 D.第四象限
(5)若0<a<1,则函数y=loga(x+5)的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(6)函数y=ax(a>1)的图象是( )

12.(1)若![]() 是定义在R上的奇函数且
是定义在R上的奇函数且![]() ,给出下列4个结论,不正确的是( )
,给出下列4个结论,不正确的是( )
A. ![]() B.
B.![]() 是以4为周期的函数 C.
是以4为周期的函数 C.![]() 的图像关于直线
的图像关于直线![]() 对称 D.
对称 D.![]()
(2) 设![]() 是
是![]() 上的奇函数,
上的奇函数,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 等于____;
等于____;
(3)定义在![]() 上的偶函数
上的偶函数![]() 满足
满足![]() ,且在
,且在![]() 上是减函数,若
上是减函数,若![]() 是锐角三角形的两个内角,则
是锐角三角形的两个内角,则![]() 的大小关系为______
___ ;
的大小关系为______
___ ;
(4)已知定义在R上的奇函数f(x)满足f(x+2)=-f(x),则,f(6)的值为 ( )
(A)-1 (B) 0 (C) 1 (D)2
(5)函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() _______
_______
友情提示
10.函数的单调性。
(1)确定函数的单调性或单调区间的常用方法:
①在解答题中常用:定义法(取值――作差――变形――定号)、导数法(在区间![]() 内,若总有
内,若总有![]() ,则
,则![]() 为增函数;反之,若
为增函数;反之,若![]() 在区间
在区间![]() 内为增函数,则
内为增函数,则![]() ,请注意两者的区别所在。
,请注意两者的区别所在。
②在选择填空题中还可用数形结合法、特殊值法等等,特别要注意![]()
![]() 型函数的图象和单调性在解题中的运用:增区间为
型函数的图象和单调性在解题中的运用:增区间为![]() ,减区间为
,减区间为![]() .
.
③复合函数法:复合函数单调性的特点是同增异减,
(2)特别提醒:求单调区间时,一是勿忘定义域;二是在多个单调区间之间不一定能添加符号“![]() ”和“或”;三是单调区间应该用区间表示,不能用集合或不等式表示.
”和“或”;三是单调区间应该用区间表示,不能用集合或不等式表示.
(3)你注意到函数单调性与奇偶性的逆用了吗?(①比较大小;②解不等式;③求参数范围).
11. 常见的图象变换
①函数![]()
![]() 的图象是把函数
的图象是把函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位得到的。
个单位得到的。
②函数![]() (
(![]() 的图象是把函数
的图象是把函数![]() 的图象沿
的图象沿![]() 轴向右平移
轴向右平移![]() 个单位得到的。、
个单位得到的。、
③函数![]() +
+![]()
![]() 的图象是把函数
的图象是把函数![]() 助图象沿
助图象沿![]() 轴向上平移
轴向上平移![]() 个单位得到的;
个单位得到的;
④函数![]() +
+![]()
![]() 的图象是把函数
的图象是把函数![]() 助图象沿
助图象沿![]() 轴向下平移
轴向下平移![]() 个单位得到的;
个单位得到的;
⑤函数![]()
![]() 的图象是把函数
的图象是把函数![]() 的图象沿
的图象沿![]() 轴伸缩为原来的
轴伸缩为原来的![]() 得到的。
得到的。
⑥函数![]()
![]() 的图象是把函数
的图象是把函数![]() 的图象沿
的图象沿![]() 轴伸缩为原来的
轴伸缩为原来的![]() 倍得到的.
倍得到的.
12. 函数的周期性。
(1)类比“三角函数图像”得:
①若![]() 图像有两条对称轴
图像有两条对称轴![]() ,则
,则![]() 必是周期函数,且一周期为
必是周期函数,且一周期为![]() ;
;
②若![]() 图像有两个对称中心
图像有两个对称中心![]() ,则
,则![]() 是周期函数,且一周期为
是周期函数,且一周期为![]() ;
;
③如果函数![]() 的图像有一个对称中心
的图像有一个对称中心![]() 和一条对称轴
和一条对称轴![]() ,则函数
,则函数![]() 必是周期函数,且一周期为
必是周期函数,且一周期为![]() ;
;
(2)由周期函数的定义“函数![]() 满足
满足![]()
![]() ,则
,则![]() 是周期为
是周期为![]() 周期函数”得:①函数
周期函数”得:①函数![]() 满足
满足![]() ,则
,则![]() 是周期为2
是周期为2![]() 的周期函数;
的周期函数;
②若![]() 恒成立,则
恒成立,则![]() ;
;
③若![]() 恒成立,则
恒成立,则![]() .
.
10.(1)![]() (2)
(2)![]() (3)
(3)![]() ;(4)(1,2)(5)
;(4)(1,2)(5)![]() (6)
(6)![]() (7)
(7)![]() . (8)
. (8)![]() (9)(0,3)。(10)
D(11) A11。(1)
(9)(0,3)。(10)
D(11) A11。(1)![]() .(2)
.(2)![]() (3)2(4)
A (5)
A (6)B
12.(1)C(2)
(3)2(4)
A (5)
A (6)B
12.(1)C(2)![]() ;(3)
;(3)![]() );(4)(B)(5)
);(4)(B)(5)![]()
函数基本概念回归课本复习材料4
今天,我怕谁之六
13.(1)已知二次函数![]() 满足条件
满足条件![]() 且方程
且方程![]() 有等根,则
有等根,则![]() =____;
=____;
(2)已知二次函数![]() 满足条件
满足条件![]() ,则
,则![]() =____;
=____;
(3)己知函数![]() ,若
,若![]() 的图像是
的图像是![]() ,它关于直线
,它关于直线![]() 对称图像是
对称图像是![]() 关于原点对称的图像为
关于原点对称的图像为![]() 对应的函数解析式是___________;
对应的函数解析式是___________;
(4)若函数![]() 与
与![]() 的图象关于点(-2,3)对称,则
的图象关于点(-2,3)对称,则![]() =______
=______
(5)已知函数图象![]() 与
与![]() 关于直线
关于直线![]() 对称,且图象
对称,且图象![]() 关于点(2,-3)对称,则a的值为______
关于点(2,-3)对称,则a的值为______
(6)已知函数![]() ,函数
,函数![]() 的图像关于点
的图像关于点![]() 成中心对称图形;
成中心对称图形;
(7) 函数![]() 与函数
与函数![]() 的图像的对称轴是______
的图像的对称轴是______
(8)已知函数![]() 的图象和函数
的图象和函数![]() 的图象关于直线
的图象关于直线![]() 对称,则a=
对称,则a=
(9)若y=f(x)定义域R,则y=f(x-1)与y=f(1-x)图象关于 对称.
(10)在下列给出的四个命题中:①y=f(x+2)与y=f(2-x)的图象关于直线x=2对称 ②若f(x+2)=f(2-x),则f(x)的图象关于直线x=2对称 ③y=f(x-2)与y=f(2-x)的图象关于y轴对称 ④若f(x-2)=f(2-x),则f(x)的图象关于y轴对称。其中正确命题的个数有(B ) A、1个B、2个 C、3个D、4个
(11)设曲线C的方程是![]() ,曲线C关于点 中心对称,函数
,曲线C关于点 中心对称,函数![]() 关于点 中心对称。
关于点 中心对称。
(12)函数![]() 图像关于
图像关于![]() 对称的函数是____________
对称的函数是____________
14. (1)函数![]() 在
在![]() 上是增函数,求
上是增函数,求![]() 的取值范围 .
的取值范围 .
(2)若y=log![]() (2-ax)在[0,1]上是x的减函数,则a的取值范围是
(2-ax)在[0,1]上是x的减函数,则a的取值范围是
(3)函数![]() 的反函数是
的反函数是
(4)已知函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]()
(5)设![]() 则
则![]() __________
__________
(6)若函数![]() =
=![]() (
(![]() >0,且
>0,且![]() ≠1)的反函数的图像过点(2,-1),则
≠1)的反函数的图像过点(2,-1),则![]() = .
= .
(7)函数![]() )的反函数是
(8)若函数
)的反函数是
(8)若函数![]() 是奇函数,则a=
是奇函数,则a=
(9)若函数![]() 在区间
在区间![]() 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是
17.(1)对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:①f(x1+x2)=f(x1)·f(x2);② f(x1·x2)=f(x1)+f(x2); ③![]() >0;④
>0;④![]() . 当f(x)=lgx时,正确结论序号是 .
. 当f(x)=lgx时,正确结论序号是 .
(2)已知函数f(x)的定义域为R,其反函数为f—1(x),若f-1(x+1)与f(x+1)互为反函数,且f(1)=2,则f(2)=____
(3)设![]() 是定义在实数集R上的函数,且满足
是定义在实数集R上的函数,且满足![]() ,如果
,如果![]() ,
,![]() ,求
,求![]() =
=
(4)已知函数![]() 的定义域是
的定义域是![]() 的一切实数,对定义域内的任意
的一切实数,对定义域内的任意![]() 都有
都有![]() ,且当
,且当![]() 时
时![]() ,则
,则![]() 是 函数;
是 函数; ![]() 在
在![]() 上是 函数;
上是 函数;
(5)已知定义域为![]() 的函数
的函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时,![]() 单调递增。如果
单调递增。如果![]() ,且
,且![]() ,则
,则![]() 的值的符号是____
的值的符号是____
(6)若![]() ,
,![]() 满足
满足![]()
![]() ,则
,则![]() 的奇偶性是______;
的奇偶性是______;
(7)若![]() ,
,![]() 满足
满足![]()
![]() ,则
,则![]() 的奇偶性是______;
的奇偶性是______;
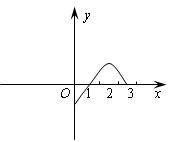
(8)已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() 的图像如右图所示,那么不等式
的图像如右图所示,那么不等式![]() 的解集是_____________;
的解集是_____________;
 (9)设
(9)设![]() 的定义域为
的定义域为![]() ,对任意
,对任意![]() ,都有
,都有![]() ,且
,且![]() 时,
时,![]() ,又
,又![]() ,①求证
,①求证![]() 为减函数;②解不等式
为减函数;②解不等式![]() .
.
(10)设 ![]()
![]() 若
若![]() ,则
,则![]() 的最大值为
的最大值为
(11)下列函数在![]() 上满足
上满足![]() 的是(C)
的是(C)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(12)已知x,y,z为正数,满足![]() 比较3x、4y、6z的大小
比较3x、4y、6z的大小
友情提示13. 函数的对称性。①满足条件![]() 的函数的图象关于直线
的函数的图象关于直线![]() 对称。
对称。
②点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ;函数
;函数![]() 关于
关于![]() 轴的对称曲线方程为
轴的对称曲线方程为![]() ;
;
③点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ;函数
;函数![]() 关于
关于![]() 轴的对称曲线方程为
轴的对称曲线方程为![]() ;
;
④点![]() 关于原点的对称点为
关于原点的对称点为![]() ;函数
;函数![]() 关于原点的对称曲线方程为
关于原点的对称曲线方程为![]() ;
;
⑤点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ;曲线
;曲线![]() 关于直线
关于直线![]() 的对称曲线的方程为
的对称曲线的方程为![]() 。特别地,点
。特别地,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ;曲线
;曲线![]() 关于直线
关于直线![]() 的对称曲线的方程为
的对称曲线的方程为![]()
![]() ;点
;点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ;曲线
;曲线![]() 关于直线
关于直线![]() 的对称曲线的方程为
的对称曲线的方程为![]() 。
。
⑥曲线![]() 关于点
关于点![]() 的对称曲线的方程为
的对称曲线的方程为![]() 。⑦形如
。⑦形如![]() 的图像是双曲线,其两渐近线分别直线
的图像是双曲线,其两渐近线分别直线![]() (由分母为零确定)和直线
(由分母为零确定)和直线![]() (由分子、分母中
(由分子、分母中![]() 的系数确定),对称中心是点
的系数确定),对称中心是点![]() 。
。
⑧![]() 的图象先保留
的图象先保留![]() 原来在
原来在![]() 轴上方的图象,作出
轴上方的图象,作出![]() 轴下方的图象关于
轴下方的图象关于![]() 轴的对称图形,然后擦去
轴的对称图形,然后擦去![]() 轴下方的图象得到;
轴下方的图象得到;![]() 的图象先保留
的图象先保留![]() 在
在![]() 轴右方的图象,擦去
轴右方的图象,擦去![]() 轴左方的图象,然后作出
轴左方的图象,然后作出![]() 轴右方的图象关于
轴右方的图象关于![]() 轴的对称图形得到。
轴的对称图形得到。
14. ![]() ,
,![]() ,
,![]() ,
, ![]() 。
。
15. 指数、对数值的大小比较:(1)化同底后利用函数的单调性;(2)作差或作商法;(3)利用中间量(0或1);(4)化同指数(或同真数)后利用图象比较。
17. 抽象函数:(1)借鉴模型函数进行类比探究。几类常见的抽象函数 :
①正比例函数型:②幂函数型:③指数函数型: ④对数函数型: ⑤三角函数型:
(2)利用函数的性质(如奇偶性、单调性、周期性、对称性等)进行演绎探究:
(3)利用一些方法(如赋值法(令![]() =0或1,求出
=0或1,求出![]() 或
或![]() 、令
、令![]() 或
或![]() 等)、递推法、反证法等)进行逻辑探究。13.(1)
等)、递推法、反证法等)进行逻辑探究。13.(1)![]() (2)
(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() (5)2(6)
(5)2(6)![]() ;
;
(7)![]() (8)-5 (9)x=1(10)B 14. (1)
(8)-5 (9)x=1(10)B 14. (1)![]() (2)(1,2)(3)
(2)(1,2)(3)![]() (4)
(4)![]()
(5)![]() (6)1/2 (7)
(6)1/2 (7)![]() (8)
(8)![]() (9)
(9)![]() 17.(1)②③(2)1(3)1;(4)偶增;(5)负数(6)奇(7)偶(8)
17.(1)②③(2)1(3)1;(4)偶增;(5)负数(6)奇(7)偶(8)![]() );(9)
);(9)![]() ).(10)
).(10)![]() . (11)(C) (12)
. (11)(C) (12)![]()