高考数学函数训练2

高考数学函数训练

考试要求：1、了解映射的概念，理解函数的概念。2、了解函数单调性、奇偶性的概念，掌握判断一些简单函数的单调性、奇偶性的方法。3、了解反函数的概念及互为反函数的函数图象间的关系，会求一些简单函数的反函数。4、理解分数指数幂的概念，掌握有理指数幂的运算性质，掌握指数函数的概念、图象和性质。5、理解对数的概念，掌握对数的运算性质，掌握对数函数的概念、图象和性质。6、能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题。

1、已知集合A = {a，b}，B = {1，2}，建立从A到B的映射共有：

　 A. 2个　　　　　　　　　　B. 4个　　　　　　　　　 C. 6个　　　　　　　　 D. 8个

2、函数是定义在无限集合D上的函数，关且满足对于任意的，

　　　①若则=　　　　　　  ；

　　　②试写出满足下面条件的一个函数存在，使得由，…，

，…组成的集合有且仅有两个元素.这样的函数可以是=　　　　　　  .

　　　　　（只需写出一个满足条件的函数）

3、已知函数f (x) = () ^x + cosx (≤x≤)，若f ( – x₁) > f (– x₂)，则有 ：

　  A. x₁ > x₂　　　　　　　　 B. x₁ < x₂　　　　　　　　C. x　　　　　　 　D. x

4、函数（其中n∈N*），K是的小数点后第n位数，

　 则的值等于:

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．4　　　　　　　　　　　　D．6

5、定义在区间[2，4]上的函数是常数）的图象过点（2，1），则函数

的值域为

A．[2，5]　　　　　　　　B．　　　　　　　 C．[2，10]　　　　　　　　D．[2，13]

6、已知函数的定义域为A，函数的定义域为B，则

　　　 A．　　　　B．　　　　　　　　 C．A = B　　　　　　　　 D．

7、已知奇函数的定义域为：，则a的值为：

　　　 A．1　　　　　　　　　　　　B．2　　　　　　　　　　　　C．3　　　　　　　　　　　　D．4

8、已知a、b、c依次是方程的实数根，则a、b、c的大小关系是

A．　　　　　B．　　　　　C．　　　　　D．

9、已知下列四组函数：① ②

　 ③　④，表示相同

　 函数的序号是:

　　　 A．③④　　　　　　　　　 B．①②　　　　　　　　　 C．①③　　　　　　　　　 D．②④

10、已知是偶函数，当时，，且当时，

　 恒成立，则的最小值是：

　　　 A．　　　　　　　　　　　B．　　　　　　　　　　　C．1　　　　　　　　　　　　D．

11、设函数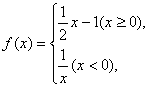若则实数的取值范围是　　　　　 .

12、若函数,则函数的图象与函数的图象的交点个数为：

　　　 A．2　　　　　　　　　　　　B．3　　　　　　　　　　　　C．4　　　　　　　　　　　　D．无数个

13、函数的单调递增区间是

　　　 A．　　　　　B．　　　 C．　　　　　D．　

14、已知的不等实根一共有　　　　 个

14、若函数满足：对于任意，都有，且

　　　 成立，则称函数具有性质M。给出下列四个函数：①，

②③，④.其中具有性质M的函数是　　　　　　 .（注：把满足题意的所有函数的序号都填上）

15．判断函数f(x)=(x－1)的奇偶性为____________________

16、已知函数（x>1）

(1)若函数在上是增函数，求实数的取值范围；

(2)解关于的不等式.

17. 通过研究学生的学习行为，专家发现，学生的注意力随着老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增；中间有一段时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，设表示学生注意力随时间(分钟)的变化规律(越大，表明学生注意力越集中)，经过实验分析得知：

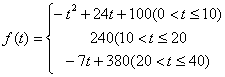
(1)讲课开始后多少分钟，学生的注意力最集中？能持续多少分钟？

(2)讲课开始后5分钟与讲课开始后25分钟比较，何时学生的注意力更集中？

(3)一道数学难题，需要讲解24分钟，并且要求学生的注意力至少达到180，那么经过适当安排，老师能否在学生达到所需的状态下讲授完这道题目？

18．设函数在区间上单调递减，求实数a的取值范围.

19、已知函数的图象与函数的图象关于点A（0，1）对称.

（Ⅰ）求函数的解析式；

（Ⅱ）求函数的单调区间.

20．已知函数

　 （1）证明：函数在上为增函数；

　 （2）用反证法证明方程没有负数根.

二、函数参考答案

1、B；2、0；；3、D；4、B；5、A；6、D；7、B；8、A；9、A；10、C；

11、；12、C；13、C；14、4；15、①③

16、解：(1) 在恒成立，则在恒成立，得。

(2) 由及x>1得，当p=-1时，，无解；

当p>-1时，且x>1，所以得1<x.

17．（1）当时，是增函数，且 ，当时，是减函数，且

所以，讲课开始10分钟，学生的注意力最集中，能持续10分钟.

（2）　 所以，讲课开始25分钟时，学生的注意力比讲课开始后5分钟更集中

（3）当时，令则

当时，令则

则学生注意力在180以上所持续的时间

所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题

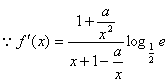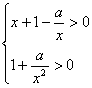18．解： ，由题意需使时，　恒成立　

即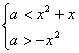 恒成立　 解得

另当a=－1时， 恒成立 （仅当x=1时“=”成立）

上递减，综上所述

19、解（I）设图象上任意一点坐标为（），则点（）关于点A（0，1）的对称点在的图象上，

　　　 ，即

（Ⅱ），

　　　 （1）当时，在 故均为的单调递增区间.

　　　 （2）当

	＋	－	－	＋
	增	减	减	增

故的单调增区间为，，

　的单调减区间为，.

20．（1）设

在上为增函数

（2）假设有负根，则有，即　 显然; 当

而，这是不可能的，即不存在的解.当矛盾，即不存在的解.综上，假设不成立，

即不存在负根.