一题多解、一题多变
参赛题目
例、
-
恒成立，求
的取值范围
解：1、当
时
2、
-
∴
变式1：已知函数
的定义域为
，求实数的取值范围。
解：由题意得
恒成立，
∴1、当 时
2、
-
∴
变式2、函数的定义域为的充要条件是什么
解：由题意得恒成立，
∴1、当 时
2、
-
∴
变式3、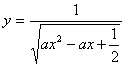
的定义域为，求实数的取值范围。
解：由题意得
恒成立，
∴1、当 时
2、
-
∴
变式4、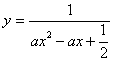
的定义域为R，求实数的取值范围。
解：由题意得-
无解即
-
或
∴
变式5、
-
的定义域为R，求的取值范围
解：由题意得恒成立，
∴1、当 时
2、
-
∴
一题多解
徐晓洲
求
的值域
法一：常数分离法
∴ 
即
-
∴值域为[
，1
法二：反解法
由
∴函数的值域为[，1
法三：判别式法
由
即：1、当
时 
故舍去
2、当
时
所以函数的值域为[，1