高考数学二轮复习三角证明与计算的综合考查
【考点聚焦】
考点1:同角的三角函数关系式;
考点2:诱导公式;
考点3:和、差、倍角公式
考点4:正弦定理、余弦定理、面积公式。
【考题形式】与倍角公式有关的计算与证明。
【考点小测】
1.cos43°cos77°+sin43°cos167°的值为
解析:cos43°cos77°+sin43°cos167°=![]() =-
=-![]() .
.
2.已知f(cosx)=cos3x,则f(sin30º)的值为 -1
3.如果![]() =
=![]() ,且
,且![]() 是第四象限的角,那么
是第四象限的角,那么![]() =
=
解:已知![]() ;
;
4.已知![]() ∈(
∈(![]() ,
,![]() ),sin
),sin![]() =
=![]() ,则tan(
,则tan(![]() )=
)=
解:由![]() 则
则![]() ,
,![]() =
=![]() ,。
,。
5![]() 已知sinα=
已知sinα=![]() ,α∈(
,α∈(![]() ,π),tan(π-β)=
,π),tan(π-β)= ![]() ,则tan(α-2β)=_____
_
,则tan(α-2β)=_____
_
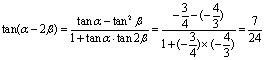
6![]() 设α∈(
设α∈(![]() ),β∈(0,
),β∈(0,![]() ),cos(α-
),cos(α-![]() )=
)=![]() ,sin(
,sin(![]() +β)=
+β)=![]() ,则sin(α+β)=______
,则sin(α+β)=______ ![]()
![]()
7. 已知![]() =2,则
=2,则![]() =
;;
=
;;![]() =
。
=
。
解:(I)∵ tan![]() =2, ∴
=2, ∴ 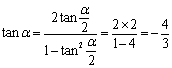 ;
;
所以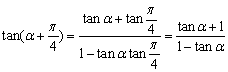 =
=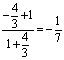 ;
;
(II)由(I), tanα=-![]() , 所以
, 所以![]() =
=![]() =
=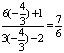 .
.
8.(江苏卷)![]() =
=
【思路点拨】本题考查三角公式的记忆及熟练运用三角公式计算求值
解:
![]()
![]()
![]()
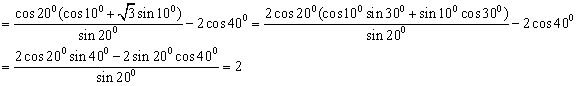
【典型考例】
【问题1】“拆项”与“添项”巧凑“和角、差角”公式
★例1★(1)![]() =
=![]() ;(2)
;(2)![]() =
=![]()
★例2★已知:![]() ,求:
,求:![]() 的值.
的值. ![]()
点评:进行三角变换的技巧常常是变角――注意角的和、差、倍、半、互余、互补关系,根据实际情况,对角进行“拆”或“添”变形,这样可以大大减少运算量.
【问题2】弦切互化
★ 例3★ P44例1 ★例4★ P44例2
P46T5(安徽卷)已知![]() (Ⅰ)求
(Ⅰ)求![]() 的值;(Ⅱ)求
的值;(Ⅱ)求![]() 的值。
的值。
解:(Ⅰ)由![]() ,得
,得![]() ,所以
,所以![]() =
=![]() 。
。
(Ⅱ)∵![]() ,∴
,∴![]() 。
。
【问题3】![]() 与
与![]() 对偶互化
对偶互化
★例5★已知![]() . (I)求sinx-cosx的值;
. (I)求sinx-cosx的值;
(Ⅱ)求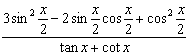 的值.
的值.
思路分析:将sinx-cosx=![]() 平方,求出sinxcosx的值,进而求出(sinx-cosx)2,然后由角的范围确定sinx-cosx的符号.
平方,求出sinxcosx的值,进而求出(sinx-cosx)2,然后由角的范围确定sinx-cosx的符号.
解法一:(Ⅰ)由![]()
即 ![]()
又![]() 故
故 ![]()
(Ⅱ)
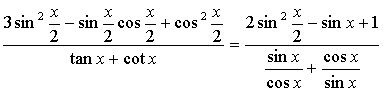
![]()
|
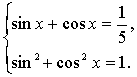
由①得![]() 将其代入②,整理得
将其代入②,整理得![]()
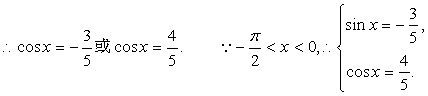
故 ![]()
(Ⅱ)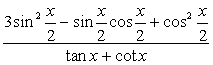
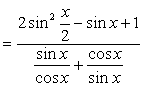
![]()
点评:本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识,以及推理和运算能力.
★例6★:已知![]() .
.
解法一:由题设条件,应用两角差的正弦公式得
![]() , 即
, 即![]() ①
①
由题设条件,应用二倍角余弦公式得
![]()
故![]() ②
②
由①式和②式得 ![]() .因此,
.因此,![]() ,由两角和的正切公式
,由两角和的正切公式
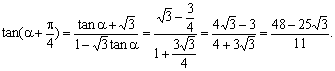
解法二:由题设条件,应用二倍角余弦公式得![]()
解得![]() 由
由![]()
由于![]() ,故
,故![]() 在第二象限,于是
在第二象限,于是![]() .
.
从而![]() ,以下同解法一.
,以下同解法一.
【问题4】向量与三角小综合
★例7★已知向量![]() ,
,
求![]() 的值.
的值.
解法一:![]()
![]()
![]()
![]()
![]()
由已知![]() ,得
,得![]() 又
又![]()
所以![]()
![]()
![]()
解法二:
![]()
![]()
![]() 由已知
由已知![]() ,得
,得![]()
![]()
![]()
★例7★.已知![]() 是三角形
是三角形![]() 三内角,向量
三内角,向量![]() ,且
,且![]() .(Ⅰ)求角
.(Ⅰ)求角![]() ;(Ⅱ)若
;(Ⅱ)若![]() ,求
,求![]() .
.
解:(Ⅰ)∵![]() ∴
∴![]()
即![]()
![]() ,
,
![]() ∵
∵![]() ∴
∴![]() ∴
∴![]()
(Ⅱ)由题知![]() ,整理得
,整理得![]()
∴![]() ∴
∴![]() ∴
∴![]() 或
或![]()
而![]() 使
使![]() ,舍去 ∴
,舍去 ∴![]()
∴![]()
![]()
![]()
![]()
![]()
★例9★.已知向量![]() ,
,
(1)
求![]() 的值;(2)若
的值;(2)若![]() 的值。
的值。
解:(1)因为![]() 所以
所以![]()
又因为![]() ,所以
,所以![]() ,
,
即![]() ;
;
(2) ![]() ,又因为
,又因为![]() ,所以
,所以 ![]() ,
,
![]() ,所以
,所以![]() ,所以
,所以![]()
★例10★.平面直角坐标系有点![]() 求向量
求向量![]() 和
和![]() 的夹角
的夹角![]() 的余弦用
的余弦用![]() 表示的函数
表示的函数![]() ;求
;求![]() 的最值.
的最值.
解:(1)
![]() ,
,
![]()
即
![]()
![]()
(2)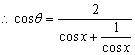 , 又
, 又 ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
【问题6】函数与三角小综合
★例11★已知函数![]() 其中
其中![]() 为参数,且
为参数,且![]() (I)当
(I)当![]() 时,判断函数
时,判断函数![]() 是否有极值;(II)要使函数
是否有极值;(II)要使函数![]() 的极小值大于零,求参数
的极小值大于零,求参数![]() 的取值范围;(III)若对(II)中所求的取值范围内的任意参数
的取值范围;(III)若对(II)中所求的取值范围内的任意参数![]() ,函数
,函数![]() 在区间
在区间![]() 内都是增函数,求实数
内都是增函数,求实数![]() 的取值范围。
的取值范围。
解:本小题主要考查运用导数研究函数的单调性及极值、解不等式等基础知识,考查综合分析和解决问题的能力。满分12分。
(I)解:当![]() 时
时![]() 则
则![]() 在
在![]() 内是增函数,故无极值。
内是增函数,故无极值。
(II)解:![]() 令
令![]() 得
得![]()
由![]() 及(I),只需考虑
及(I),只需考虑![]() 的情况。
的情况。
当![]() 变化时,
变化时,![]() 的符号及
的符号及![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
因此,函数![]() 在
在![]() 处取得极小值
处取得极小值![]() 且
且 ![]()
要使![]() 必有
必有![]() 可得
可得![]() 所以
所以![]()
(III)解:由(II)知,函数![]() 在区间
在区间![]() 与
与![]() 内都是增函数。
内都是增函数。
由题设,函数![]() 在
在![]() 内是增函数,则
内是增函数,则![]() 须满足不等式组
须满足不等式组
![]() 或
或
由(II),参数![]() 时,
时,![]() 要使不等式
要使不等式![]() 关于参数
关于参数![]() 恒成立,必有
恒成立,必有![]() 综上,解得
综上,解得![]() 或
或![]() 所以
所以![]() 的取值范围是
的取值范围是![]()
课后训练
一、选择题:
1.设函数![]() 图象的一条对称轴方程为
图象的一条对称轴方程为![]() , 则直线
, 则直线![]() 的倾斜角为
的倾斜角为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
2.已知![]() ,那么
,那么![]() A.
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3.若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(![]() )= f(
)= f(![]() ),则f(x)的解析式可以是 A.f(x)=cosx B.f(x)=cos(2x
),则f(x)的解析式可以是 A.f(x)=cosx B.f(x)=cos(2x![]() ) C.f(x)=sin(4x
) C.f(x)=sin(4x![]() ) D.f(x) =cos6x
) D.f(x) =cos6x
4.把函数![]() 的图象沿向量
的图象沿向量![]() 的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.
的方向平移后,所得的图象关于y轴对称,则m的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在![]() 内,使
内,使![]() 成立的
成立的![]() 的取值范围是
的取值范围是
(A)(![]() ) (B)(
) (B)(![]() ) (C)(
) (C)(![]() ) (D)(
) (D)(![]() )
)
6.函数y=cosx(sinx+cosx)的最小正周期为
A ![]() B
B![]() C
C ![]() D
D ![]()
7.如果![]() ,且
,且![]() ,那么
,那么![]() A.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
8.已知sin(![]() -x)=
-x)=![]() ,则sin2x的值为( )A.
,则sin2x的值为( )A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.函数f(x)=sin(x+θ)+![]() cos(x+θ)的图像关于点(5,0)对称,则θ的值是( )
cos(x+θ)的图像关于点(5,0)对称,则θ的值是( )
A.-![]() -10 B.-
-10 B.-![]() -5
C.2kπ-
-5
C.2kπ-![]() -10
D. kπ-
-10
D. kπ-![]() -5 (k∈Z)
-5 (k∈Z)
10.已知向量![]() ,
,![]() (O为原点,
(O为原点,![]() ),则向量
),则向量![]() 的长度的最大值是( )
的长度的最大值是( )
A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
11.曲线![]() 和直线
和直线![]() 在
在![]() 轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则
轴右侧的交点按横坐标从小到大依次记为P1,P2,P3,…,则![]() 等于 A.
等于 A.![]() B.2
B.2![]() C.3
C.3![]() D.4
D.4![]()
12.已知![]() 中,
中,![]() 分别为角
分别为角![]() 所对的边,且
所对的边,且![]() ,
,![]() ,
,
![]() ,则
,则![]() 的面积为(A)
的面积为(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:
13.![]() 的三内角
的三内角![]() 所对边的长分别为
所对边的长分别为![]() 设向量
设向量![]() ,
,![]() ,若
,若![]() ,则角
,则角![]() =
=
![]()
14.对于函数![]() =
=![]() (
(![]() ), 则它的值域为
;
), 则它的值域为
;
15.已知sinα=![]() ,cos(α+β)=-
,cos(α+β)=-![]() ,α、β∈(0,
,α、β∈(0,![]() ),则sin2β的值为 。
),则sin2β的值为 。
16.定义运算![]() 为:
为:![]() 例如,
例如,![]() ,则函数
,则函数![]() 的值域为 .
的值域为 .
三、解答题:
1.已知![]() ,求(1)
,求(1)![]() ;(2)
;(2)![]() 的值.
的值.
解:(1)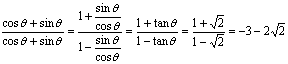 ;
;
(2) ![]()
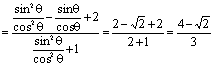 .
.
2.(上海卷)已知![]() 是第一象限的角,且
是第一象限的角,且![]() ,求
,求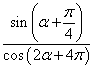 的值。
的值。
解: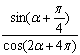 =
=
由已知可得sin![]() , ∴原式=
, ∴原式=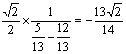 .
.
3.已知点A(2,0),B(0,2),C(cos![]() ,sin
,sin![]() ),且0<
),且0<![]() <
<![]() 。
。
(1)若![]() ,求
,求![]() 与
与![]() 的夹角;(2)若
的夹角;(2)若![]() ,求tan
,求tan![]() 的值。
的值。
解:∵(1),![]()
![]() ∴
∴![]()
又![]() ,∴
,∴![]() 又
又![]() ,∴
,∴![]() 与
与![]() 的夹角为
的夹角为![]() .
.![]() (5分)
(5分)
(2) ![]() ,
,![]() ∵
∵![]() ,∴
,∴![]()
∴![]() ∴
∴![]() ∴
∴![]() ∵
∵![]() ∴
∴![]()
又由![]() 及
及![]() 得
得![]()
由①②![]() ,
,![]() ∴
∴![]() 。
。
4.已知A (3,0),B (0,3),C![]() ①若
①若![]() =-1,求
=-1,求![]() 的值;
的值;
②若![]() ,且
,且![]() ∈(0,
∈(0,![]() ),求
),求![]() 与
与![]() 的夹角.
的夹角.
解答:(1)![]() =(
=(![]() -3,
-3,![]() ),
),![]() =(
=(![]() ,
,![]() -3),∴由
-3),∴由![]() ·
·![]() =-1,
=-1,
得(![]() -3)
-3)![]() +
+![]() (
(![]() -3)=-1,∴
-3)=-1,∴![]() +
+![]() =
=![]() ,两边平方,得1+
,两边平方,得1+![]() =
=![]() ,∴
,∴![]() =-
=-![]()
(2)![]() =(3+
=(3+![]() ,
,![]() ),∴(3+
),∴(3+![]() )2+
)2+![]() =13, ∴
=13, ∴![]() =
=![]() ,∵
,∵![]() ∈(0,π),
∈(0,π),
∴![]() =
=![]()
![]() =
=![]() , ∴
, ∴![]() ,
,
设![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() =
=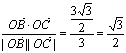 ,∴
,∴ ![]() =
=![]() 即为所求.
即为所求.
5.已知向量![]() ,
,![]() .(Ⅰ)当
.(Ⅰ)当![]() ,且
,且![]() 时,求
时,求![]() 的值; (Ⅱ)当
的值; (Ⅱ)当![]() ,且
,且![]() ∥
∥![]() 时,求
时,求![]() 的值.
的值.
解:(Ⅰ)当![]() 时,
时,![]() ,
,![]()
![]() ,
, ![]() 由
由![]() , 得
, 得![]() ,
,
上式两边平方得![]() ,因此,
,因此,![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,由
,由![]() ∥
∥![]() 得
得![]() .
.
即![]() .
. ![]() ,
,![]()
![]() 或
或 ![]() .
.
6.(安徽卷)已知![]() (Ⅰ)求
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求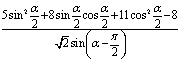 的值。
的值。
解:(Ⅰ)由![]() 得
得![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() 为所求。
为所求。
(Ⅱ)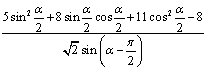 =
=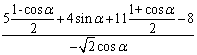
=![]() =
=![]() =
=![]() 。
。
7.(北京卷)已知函数![]() , (Ⅰ)求
, (Ⅰ)求![]() 的定义域;
的定义域;
(Ⅱ)设![]() 是第四象限的角,且
是第四象限的角,且![]() ,求
,求![]() 的值.
的值.
解:(1)依题意,有cosx¹0,解得x¹kp+![]() ,即
,即![]() 的定义域为{xxÎR,且x¹kp+
的定义域为{xxÎR,且x¹kp+![]() ,kÎZ}
,kÎZ}
(2)![]() =-2sinx+2cosx\
=-2sinx+2cosx\![]() =-2sina+2cosa
=-2sina+2cosa
由![]() 是第四象限的角,且
是第四象限的角,且![]() 可得sina=-
可得sina=-![]() ,cosa=
,cosa=![]() \
\![]() =-2sina+2cosa=
=-2sina+2cosa=![]()
8. (天津卷)已知![]() ,
,![]() .求
.求![]() 和
和![]() 的值.
的值.
本小题考查同角三角函数关系、两角和公式、倍角公式等基础知识,考查基本运算能力。
解法一:由![]() 得
得![]() 则
则![]()
因为![]() 所以
所以![]()
![]()
![]()
![]()
解法二:由![]() 得
得 ![]()
解得![]() 或
或![]() 由已知
由已知![]() 故舍去
故舍去![]() 得
得 ![]()
因此,![]() 那么
那么 ![]()
且![]()
故![]()
![]()