2007年厦门市高中毕业班适应性考试
数学（理科）试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
满分为150分，考试时间120分钟。
注意事项：
1． 考生将自己的姓名、准考证号及所有答案均填写在答题卡上；
2． 答题要求，见答题卡上的“填涂样例”和注意事项。
参考公式：
如果事件A、B互斥，那么P（A+B）=P（A）+P（B）
如果事件A、B相互独立，那么P（A·B）=P（A）·P（B）
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式：
，球的体积公式：
，其中R表示球的半径。
第I卷（选择题 共140分）
一、选择题：本大题共12个小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合
，则
等于
A．
B．
C．
D．
2．如果a<0, b>0, c
R, 那么，下列不等式中正确的是
A．
B．
C． 
D．
3．已知i、j是单位正交向量，
。那么“
”是“a//b”的
A．充要条件 B．充分不必要条件 C．必要不充分条件 D．既不充分又不必要条件
4．设Sn是等差数列{an}的前n项和，
的值为
A．
B．
C．
D．
5．函数
图象的一条对称轴是
A．
B．
C．
D．
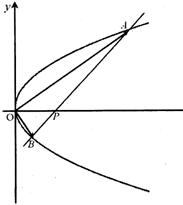
6．已知点（–3，1）是曲线
的弦AB的中点，则弦AB所在的直线方程是
A．x–y–4=0 B．x+y+2=0 C．x+2y+1=0 D．x–y+4=0
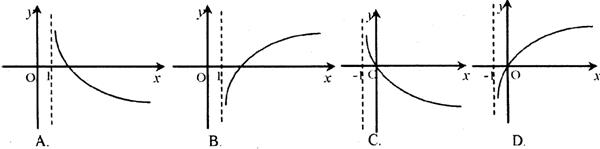
7．如果函数
是增函数，那么函数
的图像大致是
8．五名同学进行百米赛跑比赛，先后到达终点，则甲比乙先到达的情况有
A．240种 B．120种 C．60种 D．30种
9．若
，则数列的极限
为
A．3 B．1 C．
D．
10．正三棱柱ABC—A1B1C1的各棱长均为4，则A1到直线BC1的距离为
A．3 B．
C．
D．4
11．点P是椭圆
与双曲线
的交点，F 1与F 2是椭圆C1的焦点，则
等于
A．
B．
C．
D．与a的取值有关
12．国际上常用恩格尔系数（恩格尔系数=
）来衡量一个国家和地区人民生活水平的状况。根据联合国粮农组织提出的标准，恩格尔系数在60%以上为贫困，50%~60%为温饱，40%~50%为小康，30%~40%为富裕，低于30%为最富裕。一个地区今年刚好脱贫，以后每年食物支出金额和总支出金额分别以5%和10%的年增长率递增，如果该地区的生活水平要达到富裕，那么至少需要（可参考
的二项展开式进行估算）
A．5年 B．7年 C．9年 D．11年
第Ⅱ卷（非选择题 共90分）
二、填空题：本大题共4小题，每小题4分，共16分。在答题卡上相应题目的答题区域内作答。
13．复数
的虚部是__________________________。
14．
的展开式中，含x3项的系数为_____________________。
15．空间三条直线中，任何两条不共面，且两两互相垂直，直线l与这三条直线所成的角都为a，则tana=__________________________。
16．已知函数y=f（x）在R上处处可导，f（0）=0，当
0时，xf’（x）>0。给出下列四个判断：
① f（–2）< f（–1）； ② y= f（x）不可能是奇函数；
③存在区间[–a，a]，使得当
、
成立；
④ y = x f（x）在R上单调递增。
判断正确的序号是____________________。（请填上所有判断正确的序号）
三、解答题：本大题共6小题，共74分，解答题应写出文字说明、证明过程或演算步骤，在答题卡上相应题目的答题区域内作答。
17．（本小题满分12分）
在DABC中，角A、B、C所对边分别为a、b、c，且
（1） 判断DABC的形状，并加以证明；
（2） 当c=1时，求DABC面积的最大值。
18．（本小题满分12分）
甲、乙两人玩投篮游戏，规则如下：两人轮流投篮，每人至多投2次，甲先投，若有人投中即停止投篮，结束游戏。已知甲每次投中的概率为
，乙每次投中的概率为。求：
（1）乙投篮次数不超过1次的概率；
（2）记甲、乙两人投篮次数和为x，求x的分布列和数学期望。
19．（本小题满分12分）
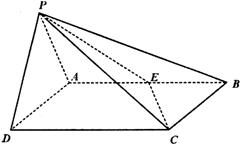
在四棱锥P—ABCD中，底面ABCD是矩形，AD=2，侧面PAD是正三角形且与底面ABCD垂直，E是AB中点，PC与平面ABCD所成角为30°。
（1） 证明：CD^平面PAD；
（2） 求二面角P—CE—D的大小；
（3） 求点D到平面PCE的距离。
20．（本小题满分12分）
已知数列{an}满足
（1）
求证：数列
是等差数列，并求{an}的通项公式；
（2）
对任何
恒成立，求实数m的取值范围。
（注：
）
21．（本小题满分12分）
已知抛物线的方程为
，过点P（2，0）的直线l与抛物线交于A、B两点，点Q满足
。
（1）
当
时，求点Q的轨迹方程；
（2）
若点Q在x轴上，且
，求直线l的斜率k的取值范围。
22．（本小题满分14分）
已知函数
。
（1） 若函数f（x）、g（x）在区间[1，2]上都为单调函数且它们的单调性相同，求实数a的取值范围；
（2）
a、b是函数H（x）的两个极值点，a<b，
。求证：对任意的x1、x2
，不等式
成立。
