苏州市第五中学2007届二轮复习测试
数学试题参考答案 2007.4.17
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的,把答案填写在答题卷相应位置上
B1、设集合![]() ,
,![]() 则
则
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
B2、已知等差数列![]() 的公差为2,若
的公差为2,若![]() 成等比数列, 则
成等比数列, 则![]() =
=
A.–4 B.–6 C. –8 D. –10
D3、在P(1,1)、Q(1,2)、M(2,3)和N![]() 四点中,函数
四点中,函数![]() 的图象与其反函数的图象的公共点只可能是点
的图象与其反函数的图象的公共点只可能是点
A.P. B.Q. C.M. D.N.
C4、给出下列函数①![]() ,②
,②![]() ③
③![]() ④
④![]() 其中是偶函数的有
其中是偶函数的有
A.1个 B.2个 C.3 个 D.4个
A5、若函数![]() 的图象过两点(-1,0)和(0,1),则
的图象过两点(-1,0)和(0,1),则
A.a=2,b=2 B.a=,b=2 C.a=2,b=1 D.a=,b=
D6、把函数y=cos2x+3的图像沿向量![]() 平移后,得到函数y=sin(2x+
平移后,得到函数y=sin(2x+![]() )的图像,则向量
)的图像,则向量![]() 的坐标是
的坐标是
A.(-![]() ,-3) B.(
,-3) B.(![]() ,3) C.(-
,3) C.(-![]() ,3) D.(
,3) D.(![]() ,-3)
,-3)
D7、球面上有三点,其中任意两点的球面距离都等于球的大圆周长的六分之一,经过这三点的小圆的周长为4π,则这个球的表面积为
A.12π B.24π C.48π D.64π
D8、过点M(1,2)的直线l将圆(x-2)2+y2=9分成两段弧,当其中的劣弧最短时,直线l的方程是
A. x=1 B. y=1 C. x-y+1=0 D. x-2y+3=0
A9、程序框图如下:
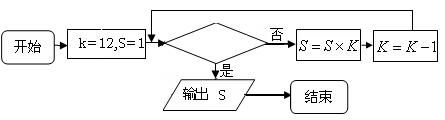
![]() 如果上述程序运行的结果为S=132,那么判断框 中应填入
如果上述程序运行的结果为S=132,那么判断框 中应填入
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
C 10、已知A箱内有红球1个和白球(n+1)个,B箱内有白球(n-1)个(n∈N,且n≥2),现随意从A箱中取出3个球放入B箱,将B箱中的球充分搅匀后,再从中随意取出3个球放入A箱,则红球由A箱移到B箱,再返回到A箱的概率等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每小题5分,共30分。不需要写出解答过程,请把答案直接填写在答题卷相应位置上。
11、某地区有![]() 、
、![]() 、
、![]() 三家养鸡场,养鸡的数量分别是
三家养鸡场,养鸡的数量分别是![]() 、
、![]() 、
、![]() 只,为了预防禽流感,现用合适的抽样方法从中抽取一个容量为
只,为了预防禽流感,现用合适的抽样方法从中抽取一个容量为![]() 只的样本检查疫情,则应从
只的样本检查疫情,则应从![]() 、
、![]() 、
、![]() 三家养鸡场分别抽取的个体数为
三家养鸡场分别抽取的个体数为![]()
12、已知向量a、b的夹角为![]() ,且a = 4,
,且a = 4,![]() ,
,
则b
= ![]() ;b在a方向上的投影等于 1 .
;b在a方向上的投影等于 1 .
13、已知三个不等式:①![]() ;②
;②![]() ;③
;③![]() .以其中两个作为条件,余下一个作为结论组成命题,则真命题的个数为 3 .
.以其中两个作为条件,余下一个作为结论组成命题,则真命题的个数为 3 .
14、若曲线![]() 在
在![]() 点处的切线与直线
点处的切线与直线![]() 平行,则
平行,则![]() 点的坐标是 (-1,0) .
点的坐标是 (-1,0) .
15、已知实数![]() 满足不等式组
满足不等式组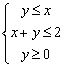 ,那么函数
,那么函数![]() 的最大值是 4
的最大值是 4
16、已知定义在R上的函数f(x)的图象关于点(-![]() ,0)成为中心对称图形,且满足
,0)成为中心对称图形,且满足
![]() 的值为 1 .
的值为 1 .
三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步
17、(本小题满分12分)
记函数![]() 的定义域为
的定义域为![]() ,
,![]() 的定义域为
的定义域为![]() .若
.若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:由![]() ≥0得:
≥0得:![]() ≥0,解得x<-1或x≥1,
≥0,解得x<-1或x≥1,
即![]()
由![]() 得:
得:![]()
由a<1得![]() ,∴
,∴![]()
∵![]() ,∴2a≥1或a+1≤-1
,∴2a≥1或a+1≤-1
即a≥![]() 或a≤-2,而a<1,∴
或a≤-2,而a<1,∴![]() ≤a<1或a≤-2
≤a<1或a≤-2
故当![]() 时,实数a的取值范围是
时,实数a的取值范围是![]()
18、(本小题满分14分)
已知函数![]()
(Ⅰ)求函数f(x)的最小正周期;
| |
(Ⅲ)若![]() 时,f(x)的反函数为
时,f(x)的反函数为![]() ,求f-1(1).
,求f-1(1).
解:(Ⅰ)![]()
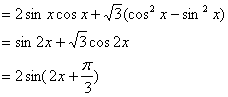
∴T=π
(Ⅱ)f(x)的减区间为![]()

(Ⅲ)![]()
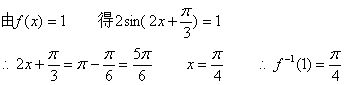
19、(本题满分14分)
一动圆与圆![]() +
+![]()
![]() =0外切,同时与
=0外切,同时与![]() 轴相切,动圆圆心的轨迹为曲线C。
轴相切,动圆圆心的轨迹为曲线C。
(Ⅰ)求曲线C的方程;
(Ⅱ)若过点(4,0)的直线![]() 与曲线C交于A,B两点,求证:以AB为直径的圆经过坐标原点。
与曲线C交于A,B两点,求证:以AB为直径的圆经过坐标原点。
曲线方程为![]()
![]() 和
和![]()
![]() 证明略
证明略
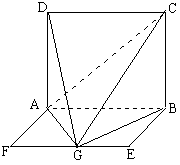 20、(本小题满分14分)如图,平面
20、(本小题满分14分)如图,平面![]() ⊥平面
⊥平面![]() ,
,![]() 是正方形,
是正方形,![]() 是矩形,
是矩形,![]() 是线段
是线段![]() 的中点,且
的中点,且![]() 点在平面
点在平面![]() 内的射影在
内的射影在![]() 上.
上.
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解:
(Ⅰ)设![]() 点在平面
点在平面![]() 内的射影为
内的射影为![]() ,则
,则![]() 在CG上,由
在CG上,由![]() ⊥平面
⊥平面![]() ,知
,知![]() ⊥
⊥![]() ,∵
,∵![]() 为正方形,∴
为正方形,∴![]() ,又平面
,又平面![]() ⊥平面
⊥平面![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]()
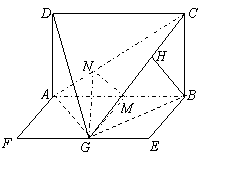 ,又
,又![]() 、
、![]()
![]() 平面
平面![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,连
,连![]() ,∵平面
,∵平面![]() ⊥平面
⊥平面![]() ,
,![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ,又
,又![]() ⊥
⊥![]() ,
,
∴![]() ⊥
⊥![]() ,∴
,∴![]() 就是二面角
就是二面角![]() 的平面角,在平面
的平面角,在平面![]() 内,由
内,由![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,![]() ,可得
,可得![]() 是
是![]() 的中点,又∵
的中点,又∵![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ,∴
,∴![]() ,设
,设![]() ,则
,则![]() ,又
,又![]() , ∴
, ∴![]()
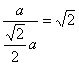 ,∴
,∴![]() ,
,
∴二面角B-AC-G的大小为![]() .
.
21、(本题满分16分)数列![]()
(Ⅰ)若数列![]() 成等比数列,求常数
成等比数列,求常数![]() 值;
值;
(Ⅱ)求数列![]() 的通项公式
的通项公式![]()
(Ⅲ)数列![]() 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由
解:(1)由![]()
∴![]()
(2)![]()
![]()
(3)设存在S,P,r![]()
![]()
即 ![]()
![]()
![]() 为偶数
为偶数
1+2![]()