一题多解、一题多变
（课本P102
）证明：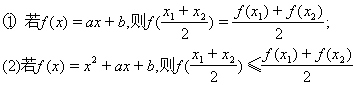
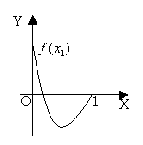变题：1、如图所示，
是定义在[0，1]上的四个函数，其中满足性质：“对[0，1]中的任意的
，任意
恒成立”的只有（ A ）
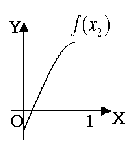
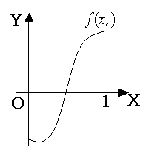
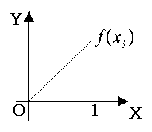
A、 
B、
C、
D、
变题2、定义在R上的函数
满足：如果对于任意
都有
则称函数是R上的凹函数。已知二次函数
（1）求证：当
时，函数是凹函数；
（2）如果
时，
，试求实数
的取值范围。
（1）证明：略
（2）实数的取值范围是
二、一题多解
不查表计算：
解法一：原式=
=
=
=
解法二：原式=
=1-
=1
解法三：原式=
=
=1
解法四：原式=
=
=1
解法五：原式=
=
=
=1