高考数学总复习测试题2
班级 姓名 学号
一，选择题（5分*10=50分）
1，函数
是
( )
A．最小正周期为
的偶函数； B．最小正周期为
的偶函数；
C．最小正周期为的奇函数； D．最小正周期为的奇函数；
2，设P为△ABC所在平面内一点，且满足
，则P是
△ABC的 （ ）
A．重心； B．垂心； C．外心； D．内心；
3，已知
与
均为单位向量，它们的夹角为
，那么
=
( )
A．
； B．1； C．
； D．4；
4，函数
在[0，
]的值域是
( )
A．[―1，1]； B．[
，1] C．[0，1] D．[―，1]
5，
，若
，则
夹角为
（ ）
A， ； B，
； C，
； D，
；
6，某个路口的交通指示灯，红灯时间为30秒，黄灯时间为10秒，绿灯时间为40秒.当你到达路口时,看见红灯的概率是 （ ）
A．
；
B．
； C．
； D．
；
7，射击场上的箭靶半径为90厘米，靶心半径为20厘米，则射中靶心的慨率为 （ ）
A，
； B， 
； C， 
； D， 
；
8，设函数
(其中
),若函数
图象的一条
对称轴为
，那么
（ ）
Ａ．； Ｂ．
； Ｃ．
； Ｄ．
；
9，已知点
、
，点P在线段AB上，且
，则点P的坐标是（ ）
A．（
，1）；
B．（
，1）； C．（―，1）； D．（―，―1）；
10，某班共有6个数学研究性学习小组,本学期初有其它班的3名同学准备加入到这6个
小组中去,则这3名同学恰好有2人安排在同一个小组的概率是 （ ）
A. 
；
B.
； C. 
；
D. 
；
二，填空题（5分*6=30分）
11，从分别写有1，2，3，4，5，6的六张卡片中任取两张，求这两张卡片上的数字之和为偶数的概率为 ．
12，已知：
＝2，
＝
，
与
的夹角为45°，要使
与
垂直，则
________
__．
13，若向量=（3，4）围绕原点按逆时针方向旋转得到向量
，则的坐标是 .
14，向量与向量的夹角为60°，且有
，则
的
值为 ，
15，△ABC中，
，
，则
_________
__．
16，函数
的单调递增区间是
；
三，解答题（10分+12分*5=70分）
17，设
（―1，―2），
（3，2），且
在
的延长线上，使
＝3
，则求点的坐标；
18，甲、乙两名篮球运动员，甲投篮命中的概率为0.8，乙投篮命中的概率为0.9，两人
是否投中相互之间没有影响。
（Ⅰ）两人各投一次，求只有一人命中的概率；（保留两位有效数字）；
（Ⅱ）两人各投两次，甲投中两次且乙投中一次的概率。（保留三位有效数字）；
19，已知
，（Ⅰ）求
的值；（Ⅱ）求
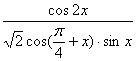的值．
20，甲箱的产品中有6个正品和3个次品， 乙箱的产品中有5个正品和3个次品．
（Ⅰ）从甲箱中任取2个产品，求这2个产品都是次品的概率；（用分数表示）
（Ⅱ）若从甲箱中任取2个产品放入乙箱中， 然后再从乙箱中任取一个产品，求取出
的这个产品是正品的概率．（用分数表示）
21，已知点A（1，0），M（1+cos2x，1)，N （2，
sin2x+2m），
，
，
是常数，且
。 （1）求
的解析式； （2）若xÎ[0,],
且的最小值为6，求的值。
22，已知函数f(x)＝2 a sin2x＋2 sinx cosx－a ，( a为常数) 的图象过点 ( 0, － ) ，
（1）求函数f(x)的值域； （2）若函数y＝f(x)的图象按向量
＝(m ，0) 作长度最短
的平移后，其图象关于y轴对称，求向量的坐标。
高考数学总复习测试题2答案：
一， D B C D D C D A B A
二，11， 
； 12， 4 ； 13，（-4， 3）； 14， 1；
15， 
；
16， [kπ+
，kπ+
], kÎZ,
三，解答题：
17， 设P（x，y），且设l=
，因为
与
方向相反，且＝3，
∴ l = ―3，有= ―3， ∴（x+1，y+2）=―3（3―x，2―y），
∴ 点的坐标为（5，4）；
18， （1），设事件A：两人各投一次，只有一人命中的事件为A，
P（A）=0.8×（1―0.9）+0.9×（1―0.8）=0.26 ，
答：两人各投一次，求只有一人命中的概率为0.26；
（2），设事件B：两人各投两次，甲投中两次且乙投中一次的事件为B，
P（B）=0.82×
×
×（1―0.9）=0.1152;
答: 两人各投两次，甲投中两次且乙投中一次的概率为0，115；
19，（1），
. ∴
tan
=,
由正切二倍角公式得tanx = 
=
=
,
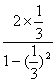（2），原式=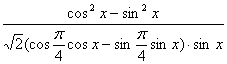
=
=
=
=
；
20，（1），设事件A：从甲箱中任取2个产品，求这2个产品都是次品的事件,
P(A)=
=
-
； 答：事件A的慨率为；
（2），设事件B：从甲箱中任取2个产品放入乙箱中， 然后再从乙箱中任取一个产品，是正品的事件,
①
：若从甲箱中任取2个放入乙箱中的是2个正品, 再从乙箱中任取一个是正品,
P () =
=
,
②
：若从甲箱中任取2个放入乙箱中的是1正品1次品, 再从乙箱中任取一个
是正品,
P () =
=
,
③
：若从甲箱中任取2个产品放入乙箱中的是2个次品, 再从乙箱中任取一个是
正品,
P () =
=
,
∴P
(B) = P ()+P ()+P ()=++=
;
答：事件B的慨率为；
21，（1），
=( cos2x,
1), 
= ( 1, sin2x+2m),
= sin2x + cos2x +2m
=2sin(2x+)+2m,
∴ y=2sin(2x+)+2m,；
（2）， 由xÎ[0,],得
≤2x+≤
, ―≤sin(2x+)≤1,
2m―1 ≤ 2sin(2x+)+2m ≤2m +2, 
=2m―1=6,
∴ =
；
22，解：⑴函数f(x)的图象过点（0，,），∴－＝2asin20＋2sin0cos0－a，
∴ a=，
∴f(x)＝2sin2x＋2sinxcosx－＝sin2x－cos2x＝2sin(2x－)，
∵－1≤sin(2x－)≤1，∴函数f(x)的值域为[－2，2]。
⑵设函数f(x)的图象上任一点(x，y)按向量＝(m，0)平移后，
y ＝2sin[2（x－m）－]＝2sin(2x－m－)，
即函数y＝2sin(2x－m－)，的图象关于y轴对称，
则必有 －m－＝， ∴即m＝－－, (k∈Z且k为奇数)，
要使m最小，则当k＝－1时，m＝， ∵ =（m，0）,
∴ 此时的坐标为（
，0）。