高考数学第一轮复习测试——集合和简易逻辑
说明：本试卷分第Ⅰ卷和第Ⅱ卷两部分，共150分；答题时间120分钟．
第I卷(共40分)
一、选择题(本大题共8小题，每小题5分，共40分，在每小题给出的四个选项中，有且只有一项是符合题目要求的)
1．设集合A = {1，2}，B = {1，2，3}，C = {2，3，4}，则(A∩B)∪C = ( )
A．{1，2，3} B．{1，2，4} C．{2，3，4} D．{1，2，3，4}
2．若命题p：x∈A∪B，则Øp是 ( )
A．x ÏA且x ÏB B．x ÏA或x ÏB
C．x ÏA∩B D．x ÎA∩B
3．定义A - B = {x xÎA且xÏB}，若M={1，2，3，4，5}，N={2，3，6}，则N - M等于( )
A．M B．N C．{1，4，5} D．{6}
4．“△ABC中，若∠C=90°，则∠A、∠B都是锐角”的否命题为 ( )
A．△ABC中，若∠C≠90°，则∠A、∠B都不是锐角
B．△ABC中，若∠C≠90°，则∠A、∠B不都是锐角
C．△ABC中，若∠C≠90°，则∠A、∠B都不一定是锐角
D．以上都不对
5．设I为全集，
是I的三个非空子集，且
，则下面论断正确的是
( )
A．
B．
C．
D．
6．“若一个数不是负数，则它的平方不是正数．”和这个命题真值相同的命题为 ( )
A．“若一个数是负数，则它的平方是正数．”
B．“若一个数的平方不是正数，则它不是负数．”
C．“若一个数的平方是正数，则它是负数．”
D．“若一个数不是负数，则它的平方是非负数．”
7．若非空集S
{1，2，3，4，5}，且若a∈S，必有(6－a)∈S，则所有满足上述条件的集合S共有
(
)
A．6个 B．7个 C．8个 D．9 个
8．命题“若△ABC不是等腰三角形，则它的任何两个内角不相等．”的逆否命题是( )
A．“若△ABC是等腰三角形，则它的任何两个内角相等”
B．“若△ABC任何两个内角不相等，则它不是等腰三角形”
C．“若△ABC有两个内角相等，则它是等腰三角形”
D．“若△ABC任何两个角相等，则它是等腰三角形”
第Ⅱ卷(非选择题，共110分)
二、填空题(本大题共6小题，每小题5分，共30分把答案填在题中横线上)
9．命题“若
”的否命题为
；
10．用“充分、必要、充要”填空：
①p或q为真命题是p且q为真命题的______条件．
②非p为假命题是p或q为真命题的______条件．
③A：x－2 <3， B：x2－4x－15<0， 则A是B的_____条件；
11．已知集合
，
，则
＝ ；
12．设集合A= {xx2+x－6=0}，B={xmx+1= 0}，则B是A的真子集的一个充分不必要的条件是___ ____．
13．已知集合A＝
－1，3，2
－1
，集合B＝3，
．若BA，则实数=
．
14．定义集合运算：A⊙B=｛z z= xy(x+y)，z∈A，y∈B｝，设集合A=｛0，1｝，B=｛2，3｝，则集合A⊙B的所有元素之和为 ．
三、解答题(共6小题，共80分)
15．(本小题满分12分) 设集合
，
(1) 若
，求实数a的取值范围；
(2) 若
，求实数a的值．
16．(本小题满分13分)已知
；
若Øp是Øq的必要非充分条件，求实数的取值范围．
17．(本小题满分13分)
已知全集为R，
．
18．(本小题满分14分) 设
，点
，但
，求
的值．
19．(本小题满分14分) 已知A={x -2 £ x £ a}，B={y y = 2x + 3，xÎA}，M={z z = x2，x ÎA}，且MÍ B，求实数a的取值范围．
20．(本题满分14分)本题共有3个小题，第1小题满分4分，第2小题满分5分，第3小题满分5分．
已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T) =Tf(x)成立．
(1) 函数f(x)= x 是否属于集合M？说明理由；
(2) 设函数f(x)=ax(a>0，且a≠1)的图象与y=x的图象有公共点，证明：
f(x)=ax∈M；
(3) 若函数f(x)=sinkx∈M，求实数k的取值范围．
高三数学同步测试参考答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | A | D | B | A | C | B | C |
二、填空题
9．若
，则
； 10．必要、充分、充要；
11．
；
12． m=
(也可为
)；
13．1 14．18
三、解答题
15．解：
，
(1)∵
，∴a≥3；
(2) ∵，∴a＝0．
16．分析：先明确
和
，再由
且 ，寻求应满足的等价条件组．
解：由
，得
．
：
=
．
由
，得
．
：
．
是 的必要非充分条件，且
， AB．
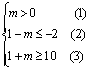即
，
注意到当时，(3)中等号成立，而(2)中等号不成立．的取值范围是
点评：分析题意，实现条件关系与集合关系的相互转化是求解本题的关键．
17．解：由已知
所以
解得
， 所以
．
由
解得
．
所以
于是
故
18．解：∵点(2，1)
，∴
①
∵(1，0)
E，(3，2)E， ∴
②
③
由①②得
；
类似地由①、③得
， ∴
．
又a，b
，∴a= -1代入①、②得b= -1．
19．解：∵B={y y = 2x + 3，xÎA}，A={x -2 £ x £ a}，
∴- 1 £ 2x + 3 £ 2a + 3，即B={y- 1 £ y £ 2a + 3}，
又M={z z = x2，x ÎA}．
∴(1) 当- 2 £ a <0时，M={za2 £ z £ 4}，
∵MÍ B，∴4 £ 2a + 3，即a ³
，不合条件，舍；
(2) 当0£ a £ 2时，M={z0 £ z £ 4}，
∵MÍ B，∴4 £ 2a + 3，即a ³，
∴£ a £ 2；
(3) 当a > 2时，M={z0 £ z £ a2}，
∵MÍ B，∴a2 £ 2a + 3，即- 1 £ a £ 3，
∴2 < a £ 3．
综上，有a的取值范围为£ a £ 3．
评析：本题主要考查分类讨论与数形结合的思想方法，这是高中数学中常用的两种方法．
20．解：(1)对于非零常数T，f(x+T)=x+T， Tf(x)=Tx． 因为对任意x∈R，x+T= Tx不能恒成
立，所以f(x)=
(2)因为函数f(x)=ax(a>0且a≠1)的图象与函数y=x的图象有公共点，
所以方程组：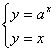
有解，消去y得ax=x，
显然x=0不是方程ax=x的解，所以存在非零常数T，使aT=T．
于是对于f(x)=ax有
故f(x)=ax∈M．
(3)当k = 0时，f(x)=0，显然f(x)=0∈M．
当k ¹ 0时，因为f(x)=sinkx∈M，所以存在非零常数T，对任意x∈R，有
f(x+T) = Tf(x)成立，即sin(kx+kT) = Tsinkx ．
因为k ¹ 0，且x∈R，所以kx∈R，kx+kT∈R，
于是sinkx ∈[- 1，1]，sin(kx+kT) ∈[- 1，1]，
故要使sin(kx+kT)=Tsinkx成立，
只有T=
，当T=1时，sin(kx+k)
= sinkx成立，则k=2mp，m∈Z．
当T= - 1时，sin(kx - k) = - sinkx 成立，
即sin(kx - k+p)= sinkx 成立，
则- k+p =2mp，m∈Z ，即k= - 2(m - 1)p，m∈Z．
综合得，实数k的取值范围是{kk= mp，m∈Z}．