高三数学第一学期期中调研模拟测试试题
(满分160分，答卷时间120分钟)
一、填空题：本大题共11小题，每小题5分，共55分．把答案填写在答题纸相应位置上．
1． 已知
，且
，则
．
2． 设集合
，集合
，则
．
3． 将
写成
时，x＋y=
．
4． 
．
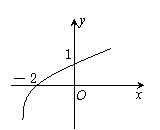
5． 已知函数
的图象如图所示，则
= ．
6． 设
则M，N，P的大小关系为 (用<联接)．
7． 若 直角三角形的三边成等比数列，则较小内角的正弦值是 ．
8． 设命题甲：
；命题乙：
，则命题甲是命题乙成立的
条
件(从“充要”，“充分不必要”，“必要不充分”，“既不充分也不必要”中选取).
9．
定义一种运算：1
1=1，
，则
．
10. 过抛物线y2＝4x的焦点F作斜率为1的直线交抛物线于A、B两点(点A在x轴上方), 若
,则
= ．
11. 已知函数
，令
(max表示最大值)，则F(x)的最
小值是 ．
二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，只有一项是符合题目要求的，请在答题纸的相应位置正确填涂．
12．不等边
的三个内角A，B，C所对的边分别是
，且
成等差
数列，则直线
与直线
的位置关系是
A．平行 B．垂直 C．重合 D．相交但不垂直
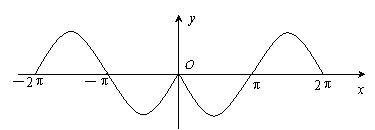13．与图中曲线对应的函数(定义域为
)是
A．
B．
C．
D．
14．已知双曲线
的焦点为
、
，点M在双曲线上，且
轴，则到直线F2M的距离为
A．
B．
C．
D.
15．已知函数
, 则
=
A．－1 B．1 C．0 D．2
三、解答题：本大题共6小题，共85分．解答应写出文字说明、证明过程或演算步骤．
16．(本题满分14分)
函数f(x)的定义域为D 
, 满足: 对于任意
，都有
，且
f(2)=1.
(1)求f(4)的值；
(2)如果
上是单调增函数，求x的取值范围.
17．(本题满分14分)
某观测站C在城A的南20˚西的方向上，由A城出发有一条公路，走向是南40˚东，在C处测
得距C为31千米的公路上B处，有一人正沿公路向A城走去，走了20千米后，到达D处，此
时
C、D间距离为21千米，问这人还需走多少千米到达A城？
18．(本题满分14分)
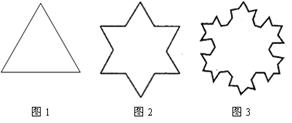
一艘太空飞船飞往地球，第一次观测时，如图1发现一个正三角形的岛屿(边长为
)；第二
次观测时，如图2发现它每边中央
处还有一正三角形海岬，形成了六角的星形；第三次观测
时，如图3发现原先每一小边的中央处又有一向外突出的正三角形海岬，把这个过程无限地
继续下去，就得到著名的数学模型——柯克岛. 把第1，2，3，
，n次观测到的岛的海岸线长
记为
，试求
的值及an的表达式.
19．(本题满分14分)
设关于x的不等式
的解集为P．
(1)当
时，求集合P；
(2)若
，且
，求实数b的值．
20. (本题满分14分)
点
是椭圆
的短轴端点，椭圆的右焦点为F，
为等边三角形，点F到椭圆右准线l的距离为1．
(1)求椭圆方程；
(2)求经过点O、F且与右准线l相切的圆的方程.
21．(本题满分15分)
数列
是公差为
的等差数列，且
的等比中项，设
．
(1)求证:
；
(2)若
，令
，
的前
，是否存在整数P、Q，使得对任意
, 都
有
，若存在，求出P的最大值及Q的最小值；若不存在，请说明理由．
参考答案及评分标准
一、填空题（5分×11＝55分）
1．
2．{(1, 1), (－2, 4)}
3．－2
4．
5．27
6．M<P<N
7．
8．必要不充分
9．
10. 
11. 
二、选择题（5分×4＝20分）
12. C 13. C 14. A 15. A
三、解答题（85分）
16．(14分)
(1)
………………………5分
(2) 3＝2＋1＝
………………………9分
因为
上是增函数，所以
………………………13分
即x的取值范围是
………………………14分
17．(14分)
根据题意得，BC=31千米，BD=20千米，CD=21千米，∠CAB=60˚． ………………2分
设∠ACD =
，∠CDB = β ．
在△CDB中，由余弦定理得
，……5分
于是
． ………………8分
．
………………………11分
在△ACD中，由正弦定理得
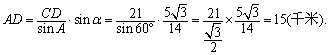………………………13分
答：此人还得走15千米到达A城． ………………………14分
18．(14分)
由题意知，
. ………………6分
因为第一个图形的边长为，从第二个图形起，每一个图形的边长均为上一个图形边长的
，所以第n个图形的边长为
；
………………9分
因为第一个图形的边数为3，从第二个图形起，每一个图形的边数均为上一个图形边数的4倍，
所以第n个图形的边数为
.
………………12分
因此，
………………14分
19．(14分)
(1)当时，原不等式为: 
.
………………2分
当
时， 
，即
解得
；
………………4分
当
时，
，即
解得 . ………………6分
所以，
.
………………7分
(2)方法1 当时，令
＝
………………9分
作函数的图像(如图).
当
，的值域为
， ………………11分
当
，的值域为
. ………………13分
所以，当不等式的解集为时，
．……14分
方法2 当时，不等式为
. ……………8分
若
，不等式的解集不可能是； ……………10分
若
，不等式为
，即x2－x＋b>0，
……………11分
由题意知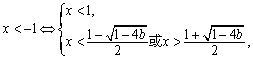
……………13分
于是有
，解得b＝－2. ……………14 分
20．(14分)
，
.
………………3分
准线l的方程：
，
所以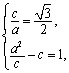
解之得
………6分
于是
.
故椭圆方程为
. ………………7分
(2)设所求圆的圆心为D，由(1)知椭圆的右准线方程为x＝4， ………………8分
因为圆D过点O，F，且与直线x＝4相切，
所以可设圆心
，半径为
，
于是圆D的方程为
,
………………11分
因为点O(0，0)在圆D上，
所以
，解得
,
所求圆的方程为
或
.
………………14分
21．(15分)
(1)证明:
，
，
………………2分
，因为
，所以
.
故 
.
………………4分
从而
.
………………6分
因为 
=
，
所以.
………………7分
(2)
当时，
，
.
………………8分
,
①
,
②
①-②, 得
=
=
,
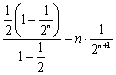……… ……11分
.
由于
，
所以数列
是递增数列，
……… ……13分
当n=1时，
的最小值为，
，所以，存在整数P、Q，使得，P的最大值为0，Q的最小值为2．
……………15分