高三数学(文科)上学期第四次月考试题
(时量:120分钟 满分:150分)
★祝考试顺利★
一、选择题:(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的,把你认为正确的结论的代号填在答题卷的表格内。)
1、设全集是实数集R,![]() ,则(CR M)∩N等于( )A.{4} B.{3,4} C.{2,3,4} D.{1,2,3,4}
,则(CR M)∩N等于( )A.{4} B.{3,4} C.{2,3,4} D.{1,2,3,4}
2、在等差数列![]() 中,若
中,若![]() ,则
,则![]() 的值为( )
的值为( )
A.14 B.15 C.16 D.17
3、已知![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
4、若函数![]() 的图像与函数
的图像与函数![]() 的图像关于点(0,1)对称,则
的图像关于点(0,1)对称,则![]() =( )
=( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
5、要使函数![]() 在[1,
2]上存在反函数,则a的取值范围是( )
在[1,
2]上存在反函数,则a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]()
![]() D. [1,2]
D. [1,2]
6、
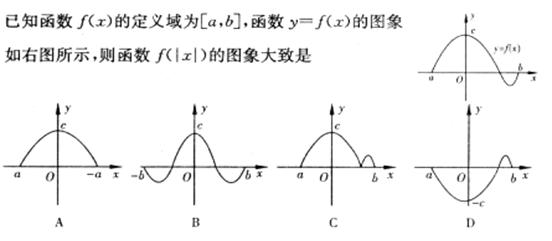 7、数列
7、数列![]() 的前n项和
的前n项和![]() 与通项
与通项![]() 满足关系式
满足关系式![]() =
=![]() ,则
,则
![]() =( )
=( )
A.-90 B.-180 C.-360 D.-400
8、已知函数![]()
![]() ,则“
,则“![]() ”是“
”是“![]() 恒成立”的( )
恒成立”的( )
A.充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分又不必要条件
9、已知函数f(x)是以2为周期的偶函数,且当![]() 的值( )
的值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.有限数列![]() ,
,![]() 为前
为前![]() 项和,定义
项和,定义![]() 为A的“凯森和”如有99项的数列
为A的“凯森和”如有99项的数列![]() 的“凯森和”为1000,则有100项的数列
的“凯森和”为1000,则有100项的数列![]() 的“凯森和”为( )
的“凯森和”为( )
A、1001 B、991 C、999 D、990
二、填空题:本大题共5小题,每小题5分,共25分。
11、已知函数f(x-1)=2x2-x,则f′(x)= 。
12.![]() 值是 。
值是 。
13.若数列![]() 满足
满足![]() ,且
,且![]() ,
,
则![]() 的值为__________。
的值为__________。
14、对于函数![]() ,给出下列命题:①f (x)有最小值;②当a=0时,
,给出下列命题:①f (x)有最小值;②当a=0时,
f (x)的值域为R;③当a>0时,f (x)在区间![]() 上有反函数;④若f (x)在区间
上有反函数;④若f (x)在区间![]() 上是增函数,则实数a的取值范围是
上是增函数,则实数a的取值范围是![]() 。上述命题中正确的是 (填上所有正确命题序号) 。
。上述命题中正确的是 (填上所有正确命题序号) 。
15、在公差为![]() 的等差数列
的等差数列![]() 中,若
中,若![]() 是
是![]() 的前
的前![]() 项和,则数列
项和,则数列
![]() 也成等差数列,且公差为
也成等差数列,且公差为![]() ,类比上述结论,相应地在公
,类比上述结论,相应地在公
比为![]() 的等比数列
的等比数列![]() 中,若
中,若![]() 是数列
是数列![]() 的前
的前![]() 项积,则有 。
项积,则有 。
三、解答题:本大题共6小题,共75分. 解答应写出文字说明,证明过程或演算步骤。
16、(本题满分12分)已知函数![]()
(1)求![]() ; (2)若
; (2)若![]() ,求
,求![]() .
.
17、(本题满分12分) 已知命题![]() 在
在![]() 上有意义;
上有意义;
命题![]() 数列
数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,均有
,均有![]()
![]() 恒成立。若命题p与q有且仅有一个是正确的,求实数t的范围。
恒成立。若命题p与q有且仅有一个是正确的,求实数t的范围。
18、(本题满分12分)某铁路指挥部接到预报,24小时后将有一场超历史记录的大暴雨,为确
保万无一失,指挥部决定在24小时内筑一道归时堤坝以防山洪淹没正在紧张施工的遂道工
程。经测算,其工程量除现有施工人员连续奋战外,还需要20辆翻斗车同时作业24小时。
但是,除了有一辆车可以立即投入施工外,其余车辆需要从各处紧急抽调,每隔20分钟有
一辆车到达并投入施工,而指挥部最多可组织25辆车。问24小时内能否完成防洪堤坝工程?
并说明理由.
19、(本题满分12分) 记函数f(x)的定义域为D,若存在x0∈D,使f(x0)=x0成立,则称以
(x0,y0)为坐标的点是函数f(x)的图象上的“稳定点”.
(1)若函数f(x)=![]() 的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
的图象上有且只有两个相异的“稳定点”,试求实数a的取值范围;
(2)已知定义在实数集R上的奇函数f(x)存在有限个“稳定点”,求证:f(x)必有奇数个“稳定点”.
20、(本题满分13分) 设![]() 、
、![]()
![]() 是函数
是函数![]() (
(![]() )的两个极值点,其中a, b为实常数.
)的两个极值点,其中a, b为实常数.
(Ⅰ)若![]() ,对于区间[-1,1]上任意两个自变量的值x1,x2,都有
,对于区间[-1,1]上任意两个自变量的值x1,x2,都有
f(x1)-f(x2)≤k恒成立, 求实数k的最小值。
(Ⅱ)若![]() ,求
,求![]() 的最大值。
的最大值。
21、(本题满分14分)
设![]() 有唯一解,
有唯一解,![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若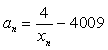 且
且![]() ,求证:
,求证:![]() ;
;
(Ⅲ)是否存在最小整数![]() ,使得对于任意
,使得对于任意![]() ,有
,有![]() 成立,若存在,求出
成立,若存在,求出![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
 汉寿一中2008届高三第三次月考
汉寿一中2008届高三第三次月考
数学(文科)试题
(时量:120分钟 满分:150分)
| 第Ⅰ卷 选择题 | ||||||||||||||||||||||
| 一、选择题:(本大题满分50分)
| ||||||||||||||||||||||
| 第Ⅱ卷 非选择题 | ||||||||||||||||||||||
| 二、填空题: (本大题满分25分)
11题 12题
13题 14题 15题 | ||||||||||||||||||||||
| 三、解答题(本大题满分75分) 16题(本小题满分12分) 解:
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
| ||||||||||||||||||||||
| 17题(本小题满分12分) 解:
| ||||||||||||||||||||||
| 18题(本小题满分12分) 解:
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
| ||||||||||||||||||||||
| 19题(本小题满分12分) 解:
| ||||||||||||||||||||||
| 20题(本小题满分13分) 解:
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效 | ||||||||||||||||||||||
| 21题(本小题满分14分) 解:
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效 |
数学(文科)试题参考答案
一、选择题答题栏:(本大题共10小题,每小题5分,共50分。)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | B | B | C | B | C | B | A | B |
二、填空题答题栏:(本大题共5小题,每小题5分,共25分。)
11、![]() 12、1
12、1
13、102 14、②③
15、![]()
三、解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16、解(1)![]() …………2分
…………2分
![]() …………………………………………………………4分
…………………………………………………………4分
![]() ……………………………………6分
……………………………………6分
(2)由![]() 得
得![]()
即![]() ……………………………………………………8分
……………………………………………………8分
![]() …………………………………………………9分
…………………………………………………9分
又![]() ……………………………………11分
……………………………………11分
![]() ………………………………………………………………12分
………………………………………………………………12分
17、解:对于p:![]() ,
,![]() 恒成立,即
恒成立,即![]() ,
,![]() 恒成立.
恒成立.![]() ;
(5分)
;
(5分)
对于q:![]()
![]()
![]() 解得
解得![]()
![]()
![]() . (10分)
. (10分)
故命题p和q有且仅有一个命题成立的t的取值范围是![]() . (14分)
. (14分)
18、解:由20辆车同时工作24小时可完成全部工程可知:每辆车,每小时的工作效率为![]() ,设从第一辆车投入施工算起,各车的工作时间为a1,a2,…, a25小时,依题意它们组成公差
,设从第一辆车投入施工算起,各车的工作时间为a1,a2,…, a25小时,依题意它们组成公差![]() (小时)的等差数列,且
(小时)的等差数列,且
![]() ,化简可得
,化简可得![]() .
.
解得![]() .
.
可见a1的工作时间可以满足要求,即工程可以在24小时内完成.
19、解:(1)设P(x1,y1),Q(x2,y2)(x1≠x2)是函数f(x)=![]() 的图象上的两个“稳定点”,
的图象上的两个“稳定点”,
∴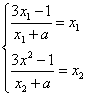 ,即有x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a). 4分
,即有x12+ax1=3x1-1(x1≠-a),x22+ax2=3x2-1(x2≠-a). 4分
∴x1、x2是方程x2+(a-3)x+1=0两根,且∵x1, x2≠-a,∴x≠-a,
∴方程x2+(a-3)x+1=0有两个相异的实根且不等于-a.
∴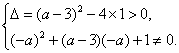
∴a>5或a<1且a≠-![]() .
.
∴a的范围是(-∞,-![]() )∪(-
)∪(-![]() ,1)∪(5,+∞). …………8分
,1)∪(5,+∞). …………8分
(2)∵f(x)是R上的奇函数,∴f(-0)=-f(0),即f(0)=0.∴原点(0,0)是函数f(x)的“稳定点”,若f(x)还有稳定点(x0,y0),则∵f(x)为奇函数,f(-x0)=-f(x0),f(x0)=x0,∴f(-x0)=-x0,这说明:(-x0,-x0)也是f(x)的“稳定点”.
综上所述可知,f(x)图象上的“稳定点”除原点外是成对出现的,而且原点也是其“稳定点”,∴它的个数为奇数.
20、(1)∵![]() 是函数
是函数![]() 的两个极值点,
的两个极值点,
∴![]() ,
,![]() ,解得
,解得![]() ………………2分
………………2分
∴![]() 。…………………………………………………………3分
。…………………………………………………………3分
∵ 当-1<x<1时,f′(x)<0,故f(x)在区间[-1,1]上为减函数,
∴ fmax(x)=f(-1)=21,fmin(x)=f(1)=-39.
∵ 对于区间[-1,1]上任意两个自变量的值x1,x2,
都有 : f(x1)-f(x2)≤fmax(x) -fmin(x) ………………………5分
∴ f(x1)-f(x2)≤fmax(x)-fmin(x)=21-(-39)=60
∴ k≥60………………………………………………………………………6分
(2).∵![]() 是函数
是函数![]() 的两个极值点,∴
的两个极值点,∴![]() 。
。
∴![]() 是方程
是方程![]() 的两根。
的两根。
∵![]() ,∴
,∴![]() 对一切
对一切![]() 恒成立。
恒成立。![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() 。……………………………………………………………7分
。……………………………………………………………7分
∴![]() 。……………………8分
。……………………8分
由![]() 得
得![]() ,∴
,∴![]() 。…………9分
。…………9分
∵![]() ,∴
,∴![]() ,∴
,∴![]() 。……………………………………10分
。……………………………………10分
令![]() ,则
,则![]() 。
。
当![]() 时,
时,![]() ,∴
,∴![]() 在(0,4)内是增函数;
在(0,4)内是增函数;
当![]() 时,
时,![]() ,∴
,∴![]() 在(4,6)内是减函数。
在(4,6)内是减函数。
∴当![]() 时,
时,![]() 有极大值为96,∴
有极大值为96,∴![]() 在
在![]() 上的最大值是96,
上的最大值是96,
∴![]() 的最大值是
的最大值是![]() 。………………………………………………………………13分
。………………………………………………………………13分
21、(1)![]()
(2)![]()
(3)存在,![]()