高考数学复习三角练习测试题
第Ⅰ卷(选择题，共40分)
一、选择题 (本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的,请将正确答案代号填在下面的答题框内.)
1.已知sin(α+β)cosβ-cos(α+β)sinβ=
，且α在第二象限，则tan
A.
或－3
B.3 C. D.3或－
2.在△ABC中，若a cos A=b cos B，则这个三角形的形状是
A.锐角三角形 B.直角三角形
C.等腰三角形 D.等腰三角形或直角三角形
3.下列四个函数：①y=tanｘ，②y=lgx，③y=sin(x+
)，④y＝2x，其中是偶函数，又在区间(-1，1)内连续的函数的是
A.②③ B.①②③ C.①③ D.②④
4.函数y=sin(2x+
)的图象可由函数y=sin2x的图象经过平移而得到，这一平移过程可以是
A.向左平移
B.向右平移
C.向左平移
D.向右平移
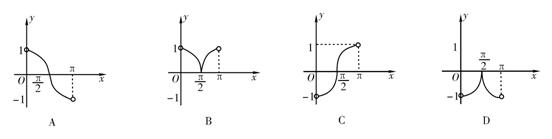
5.函数y＝sinxcotx（0<x<π）的图像的大致形状是
6.y=log
sin(2x+
)的单调递减区间是
A.［kπ－，kπ］(k∈Z)
B.(kπ－
，kπ+)(k∈Z)
C.［kπ－
，kπ+］(k∈Z) D.［kπ－，kπ+］(k∈Z)
7．定义在R上的偶函数f(x)满足f(x)=f(x+2)，当x∈［3，4］时，f(x)=x－2，则
A.f(sin
)<f(cos)
B.f(sin)>f(cos)
C.f(sin1)<f(cos1)
D.f(sin
)>f(cos)
8.设y=f(t)是某港口水的深度y（米）关于时间t（时）的函数，其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：
| t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y | 12 | 15.1 | 12.1 | 9.1 | 11.9 | 14.9 | 11.9 | 8.9 | 12.1 |
经长期观察，函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωx+φ)的图象.下面
的函数中，最能近似表示表中数据间对应关系的函数是
A.y=12+3sint，t∈［0，24］
B.y=12+3sin(t+π)，t∈［0，24］
C.y=12+3sint，t∈［0，24］
D.y=12+3sin(t+)，t∈［0，24］
第Ⅱ卷(非选择题，共60分)
二、填空题 (本大题共4小题，每小题3分，共12分.把答案填在下面的横线上.)
9．求值：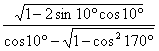
=
.
10.函数y=cos4x-sin4x的单调增区间是 .
11．已知3sin2α+2sin2β-2sinα=0，则cos2α+cos2β的取值范围是 .
12.关于函数y1=2sin(x+φ)(φ为常数)和函数y2= -cos(2x+)(x∈R)有下列命题：
（1）设y1和y2的最小正周期分别是T1和T2，那么T1+T2=3π；
（2）当φ=时，在区间(-，)上，y１和y２都是增函数；
（3）当φ=0时，y1+y2的最大值为
；
（4）当φ=时，y1+y2为偶函数.
其中正确命题的序号是 （把你认为正确的命题的序号都填上）。
三、解答题 (本大题4小题，共48分.解答应写出必要的文字说明、证明过程或演算步骤.)
13. (本小题满分12分)
求值：
14．(本小题满分12分)
已知sin(+2α)·sin(-2α)=
，α∈(，)，求2sin2α+tanα-cotα-1的值.
15．(本小题满分12分)
已知函数f(x)=2acos2x+bsinxcosx
，且f(0)= ，f()=.
(1)求f（x）的最小正周期；
(2)求f（x）的单调递减区间；
(3)函数f（x）的图象经过怎样的平移才能使其对应的函数成为奇函数？
16.(本小题满分12分)
设二次函数f(x)=x2+bx+c(b，c∈R)，已知不论α，β为何实数恒有f(sinα)≥0,f(2+cosβ)≤0.
（1）求证：b+c= -1；
（2）求证：c≥3；
（3）若函数f(sinα)的最大值为8，求b，c的值.
参考答案
1.B
sin(α+β)cosβ-cos(α+β)sinβ=sinα=，且α在第二象限，所以cosα= -
，则tan=
=3.
2.D因为2RsinAcosA=2RsinBcosB，则sin2A=sin2B，所以2A=2B或2A=π-2B，可得A=B或A+B=，故选D.
点评：由三角形中恒等式判断三角形的形状，一般有两种思路：一是将角化边，用边的关系进行判断；二是将边化角，用角的关系来判断.应充分运用三角形中的内角和定理、正余弦定理进行边角互化.
3.C
因为y=lgx的定义域为(-∞，0)∪(0，+∞)，则y=lgx不是区间(-1，1)的连续函数，又y＝2x显然不是偶函数，只有y=tanx和y=sin(x+)两个条件都满足，故选C.
点评：此题相当于多元选择题，应注意将每个命题的真假判断准确，才能选出正确答案. 4.A 由y=sin2x
y=sin(2x+).故选A.
5.B
法1：y=sinxcotx(0<x<π)=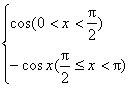
故选B.
法2：0<x<π，所以y＝sinxcotx≥0，选B.
6.B
由sin(2x+)>0且2kπ<2x+<2kπ+ (k∈Z)，解得x∈(kπ－，kπ+)(k∈Z)，选B.
7.C ∵当0<x<1时，∴4-x∈(3，4)，f(x)=f(-x)=f(4-x)=(4-x)-2=2-x，此时f(x)为减函
数，检验选择支，由于0<cos1<sin1<1，只有C正确.
点评：此题综合考查函数奇偶性、周期性、单调性、三角函数的性质、不等式的知识，除上述方法外，还可应用f(x)的图象来判断也较方便.
8.A
由表中数据可得ymax=15.1，ymin=8.9，故k=
=12.
T=3-0，∴T=12 又T=
，∴ω=，故选A.
点评：本题考查学生运用三角函数图象与性质来解决实际问题的能力，学生应准确理解三角函数y=k+Asin(ωx+φ)的图象和性质.
9.1解：=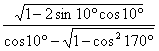
=
=
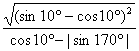点评：注意灵活使用同角三角函数的基本关系式的变形式，即“1”的妙用，这也是三角函数式化简过程中常用的技巧之一，另外，注意及时使用诱导公式和三角函数图象和性质：当α∈［0，］时，sinα＜cosα.
10.解：y=cos4x-sin4x=(cos2x-sin2x)(cos2x+sin2x)=cos2x-sin2x=cos2x
当2x∈［2kπ-π，2kπ］，即x∈［kπ-，kπ］(k∈Z)时y=cos4x-sin4x递增，所以其增区间为［kπ-，kπ］(k∈Z).
11.解：由已知得，2sin2β= -3sin2α+2sinα
∵sin2β∈［0，1］，∴0≤-3sin2α+2sinα≤2，解得0≤sinα≤
.
∵cos2α+cos2β=2-sin2α-sin2β
=2-sin2α-
=sin2α-sinα+2= (sinα-1)2+，
∵0≤sinα≤ ∴cos2α+cos2β∈［
，2］
点评：求函数的值域、单调区间、奇偶性、周期性、解不等式等都要切记函数的生命线：定义域.否则，错误将会“趁虚而入”，若在本例中不注意深挖定义域：0≤sinα≤，则会得到错误结果：cos2α+cos2β∈［，
］.
12.解：(1)∵T1=2π，T2=π，则T1+T2=3π;
(2)当φ=时，在区间(-，)上，x+φ=x+∈(0，)，y1为增函数；
在区间(-，)上，2x+∈(0，)，y2也为增函数；
（3）显然y1的最大值为2，y2的最大值为0.5，y1+y2的最大值为2.5；
（4）当φ=时，y1=2cosx为偶函数，y2= -cos(2x+)(x∈R)为非奇非偶函数，y1+y2为非奇非偶函数.
由上可知正确命题的序号是（1），（2），（3）.
13.解：原式=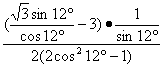
=
=
=
.
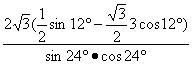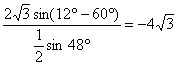点评：知角求值问题中应充分利用三角恒等变形技巧如本题中常值的代换、三角公式的逆用及变形用、设辅助角进行变形等，这些技巧往往要结合使用.
14.解：由sin(+2α)·sin(-2α)=sin(+2α)·cos(+2α)=sin(+4α)=cos4α=，
则cos4α=.又α∈(，)，所以α=
.
于是2sin2α+tanα-cotα-1= -cos2α+
=-cos2α+
= -(cos2α+2cot2α)=-(cos
+2cot)= -(-2
)=.
点评：三角函数中的条件求值问题，一般应将条件和所求结果式子化简，并注意将所求的角或三角函数用已知的角或三角函数表示出.
15.解：(1)由f(0)=
，得2a-=，∴2a=，则a=.
由f()=，得+
-=，∴b=1，
∴f(x) =cos2x+sinxcosx -
=cos2x+sin2x=sin(2x+).
∴函数f(x)的最小正周期T=
=π.
(2)由+2kπ≤2x+≤
+2kπ，得+kπ≤x≤
π+kπ，
∴f（x）的单调递减区间是［+kπ，π+kπ］(k∈Z)．
(3)∵f(x)=sin2(x+)，∴奇函数y=sin2x的图象左移即得到f(x)的图象，故函数f(x)的图象右移后对应的函数成为奇函数．
点评：本题综合考查三角函数恒等变形的技巧、三角函数单调性的求法、周期的求法、三角函数图象的变换、待定系数法等有关知识.用待定系数法准确a、b的值并化简求出f(x)=sin(2x+)是解决本题的关键.
16.解(1)∵sinα∈［-1，1］，2+cosβ∈［1，3］，
又f(sinα)≥0，f(2+cosβ)≤0恒成立.∴f(1)≥0，f(1)≤0，即f(1)=0恒成立.
∴1+b+c=0，即b+c= -1.
（2）f(3)≤0，∴9+3b+c≤0，∴9+3(-1-c)+c≤0，∴c≥3.
（3）由（1）、（2）可知b=-1-c≤-4，∴f(x)在［-1，1］上为减函数，
∴8=f(-1)=1-b+c ①， 又b+c= -1 ②，
由①，②可得 b= -4，c=3.
点评：赋值法在解决有关恒成立问题时经常用到，利用函数的单调性往往能使问题得以顺利解决.