高考数学复习—不等式练习试题
第Ⅰ卷 (选择题 共50分)
一、选择题(10×5′=50′)
1.已知方程2x+x=0的实根为a,log2x=2-x的实根为b,log![]() x=x的实根为c,则 ( )
x=x的实根为c,则 ( )
A.b>c>a B.c>b>a C.a>b>c D.b>a>c
2.若a>0,a2-2ab+c2=0,bc>a2,则 ( )
A.a>b>c B.b>c>a C.c>b>a D.b>a>c
3.在满足面积与周长的数值相等的所有直角三角形中,面积的最小值是 ( )
A.(![]() -1)2
B.2(
-1)2
B.2(![]() +1)2 C.3(
+1)2 C.3(![]() -1)2 D.4(
-1)2 D.4(![]() +1)2
+1)2
4.设a、b∈R,那么“a2+b2<1”是“ab+1>a+b”的 ( )
A.充要条件 B.必要非充分条件
C.充分非必要条件 D.既非充分也非必要条件
5.两个集合A与B之差记作 “A/B”,定义为:A/B={xx∈A,且x![]() B}, 如果集合A={xlog2x<1,x∈R},集合B={xx-2<1,x∈R},那么A/B等于 ( )
B}, 如果集合A={xlog2x<1,x∈R},集合B={xx-2<1,x∈R},那么A/B等于 ( )
A.{xx≤1} B.{xx≥3} C.{x1≤x<2} D.{x0<x≤1}
6.已知log![]() x1=logax2=log(a+1)x3>0,0<a<1,则x1、x2、x3的大小关系是 ( )
x1=logax2=log(a+1)x3>0,0<a<1,则x1、x2、x3的大小关系是 ( )
A.x3<x2<x1 B.x2<x1<x3 C.x1<x3<x2 D.x2<x3<x1
7.设a、b、c是一个长方体的长、宽、高,且a+b-c=1,已知该长方体对角线长为1,且b>a,则高c的取值范围是 ( )
A.![]() B.
B.![]() C.(0,1) D.
C.(0,1) D.![]()
8.某债券市场常年发行债券,A种债券面值为1 000元,一年到期本息和为1 040元;B种债券面值为1 000元,但买入价为960元,一年到期本息和为1 000元;C种面值为1 000元,半年到期本息和为1 020元.设这三种债券的年收益率分别为a、b、c,则a、b、c的大小关系是 ( )
A.a=c且a<b B.a<b<c C.a<c<b D.c<a<b
9.设an=![]() +
+![]() +…+
+…+![]() ,则对任意正整数m、n(m>n)都成立的不等式是 ( )
,则对任意正整数m、n(m>n)都成立的不等式是 ( )
A.am-an<![]() B.am-an>
B.am-an>![]() C.am-an<
C.am-an<![]() D.am-an>
D.am-an>![]()
10.若关于x的不等式x2-ax-6a<0有解且解区间长不超过5个单位长,则a的取值范围是 ( )
A.-25≤a≤1 B.-25≤a<0或1≤a<24
C.a≤-25或a≥1 D.-25≤a<-24或0<a≤1
二、填空题(4×4′=16′)
11.使log2(-x)<x+1成立的x的取值范围是 .
12.对于|m|≤1的一切实数m,使不等式2x-1>m(x2-1)都成立的实数x的取值范围是 .
13.已知关于x的不等式(a+b)x+(2a-3b)<0的解集为(-3,+∞),则log6ba2= .
14.不等式(x-2)![]() ≥0的解集是
.
≥0的解集是
.
三、解答题(4×10′+14′=54′)
15.已知ai∈R+,![]() =S,求证:
=S,求证:![]() .
.
16.甲、乙两地相距skm,汽车从甲地匀速行驶到乙地,速度不得超过ckm/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成,可变部分与速度v(km/h)的二次方成正比,且比例系数为b,固定部分为a元.
(1)把全部运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大的速度行驶?
17.不等式(-2)xa-3x-1-(-2)x<0对于任意正整数x恒成立,求实数a的取值范围.
18.设f (x)=x2+bx+c(b、c为常数),方程f (x)-x=0的两个实根为x1、x2,且满足x1>0,x2-x1>1.
(1)求证:b2>2(b+2c);
(2)设0<t<x1,试比较f (t)与x1的大小;
(3)若当x∈[-1,1]时,对任意的x都有f (x)≤1,求证:1+b≤2.
19.已知函数f (x)对任意的实数x、y都有f (x+y)=f (x)+f (y)+2y(x+y)+1,且f (1)=1.
(1)若x∈N*,试求f (x)的表达式;
(2)若x∈N*且x≥2时,不等式f (x)≥(a+7)x-(a+10)恒成立,求实数a的取值范围.
不等式练习参考答案
一、选择题
1.A 由已知得a<0,b∈(1,2),c∈(0,1),故b>c>a.
2.B 由bc>a2知b,c同号.
∵a2+c2=2ab,a2+b2≥2ab,∴b2≥c2.
∵a>0,∴b>0.∴c>0.∴b≥c.
若b=c,可推出a=b=c,这与bc>a2矛盾.
∴b>c.∴b2>bc>a2.∴a<b.∴a(a-b)<0.
∵a2-2ab+c2=0,∴a2-2ab+bc>0,a2-ab>ab-bc. ∴b(a-c)<a(a-b)<0.∴a-c<0.
∴a<c.∴b>c>a.
3.D 设两条直角边的长为a、b,则![]() ab=a+b+
ab=a+b+![]() .
.
∴![]() ab≥2
ab≥2![]() +
+![]() ,整理,得
,整理,得![]() ab≥4(
ab≥4(![]() +1)2.
+1)2.
即面积的最小值为4(![]() +1)2.
+1)2.
4.C ab+1>a+b![]() (a-1)(b-1)>0
(a-1)(b-1)>0![]()
![]() 或
或![]()
a2+b2<1![]() a<1且b<1
a<1且b<1![]() -1<a<1,-1<b<1
-1<a<1,-1<b<1![]() (a-1)(b-1)>0
(a-1)(b-1)>0![]() ab+1>a+b.
ab+1>a+b.
易知ab+1>a+b![]() a2+b2<1.
a2+b2<1.
即a2+b2<1是ab+1>a+b的充分非必要条件.
5.D 本题是一道信息题,考查考生阅读理解能力和自学能力.解题的关键在于理解“A/B”,联立不等式,得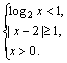 解得0<x≤1,故选D.
解得0<x≤1,故选D.
6.D 取a=![]() 满足条件,则log4x1=log
满足条件,则log4x1=log![]() x2=log
x2=log![]() x3>0.画出图象后知选D.
x3>0.画出图象后知选D.
7.D 依题意有a2+b2+c2=1,即a2+b2=1-c2,a+b=1+c,
∴ab=![]() ,易知a、b是关于x的方程x2-(1+c)x+c2+c=0的两个不相等的正根,
,易知a、b是关于x的方程x2-(1+c)x+c2+c=0的两个不相等的正根,
∴依判别式Δ=(1+c)2-4(c2+c)>0,可解得0<c<![]() ,故选D.
,故选D.
8.C 分别对三种债券的年收益率进行计算:
对A:a=![]()
对B:b=![]()
对C:前半年的增长率为![]() ,且依题意,
,且依题意,
在后半年增长的钱数为1 020×![]()
∴c=![]() 显然大小关系为:a<c<b.
显然大小关系为:a<c<b.
9.C ∵am-an=![]()
<![]() ,故选C.
,故选C.
10.D 由题设得![]() (*)其中x1、x2是方程x2-ax-6a=0的两根,解(*)式得
(*)其中x1、x2是方程x2-ax-6a=0的两根,解(*)式得
-25≤a<-24或0<a≤1,故选D.
二、填空题
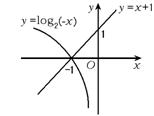
11.(-1,0) 分析 用代数方法很难解决此类超越不等式问题,
|
解 在同一坐标系中作出y=log2(-x)及y=x+1的图象,由
图象知,-1<x<0时,log2(-x)<x+1,故x的取值范围是(-1,0).
12.(![]() -1,2) 将题目中的x与m互换,即问题可化为求使不
-1,2) 将题目中的x与m互换,即问题可化为求使不
等式2m-1>x(m2-1),即(1-m2)x+(2m-1)>0,在[-1,1]上恒成立
的实数m的取值范围.令f (x)=(1-m2)x+(2m-1),则有
![]() 或
或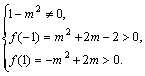
即m=1或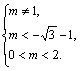 或m>
或m>![]() -1,0<m<2.
-1,0<m<2.
所以![]() -1<m<2.故原题中实数x的取值范围是(
-1<m<2.故原题中实数x的取值范围是(![]() -1,2).
-1,2).
13.2 由已知,得(a+b)x<3b-2a.
若a+b>0,不等式的解集为![]() ;
;
若a+b<0,不等式的解集为![]() .
.
由已知不等式的解集为(-3,+∞)得a+b<0,
且![]() .解得a=-6b<0.
.解得a=-6b<0.
∴log6ba2=log6b(-6b)2=2.
14.{xx=-1或x≥3} 由于(x-2)![]() ≥0,
≥0,
当x2-2x-3=0时,x1=-1,x2=3,适合不等式.
当x2-2x-3>0时,x-2≥0,此时x>3,
故原不等式的解集为{xx=-1或x≥3}.
三、解答题
15.证明 构造a=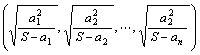 ,b=(
,b=(![]() ,
,![]() ,…,
,…,![]() ).
).
因为a·b=a1+a2+…+an=S,
|a|=![]() ,|b|=
,|b|=![]() .
.
所以S≤![]() ·
·![]() .
.
故![]() ≥
≥![]() .
.
16.解 (1)依题意,汽车从甲地匀速行驶到乙地所用时间为![]() ,
,
全程运输成本为y=a·![]() +bv2·
+bv2·![]() =s
=s![]()
∴所求函数及其定义域为y=s![]() v∈(0,c)
v∈(0,c)
(2)依题意知s、a、b、v均为正数 ∴y=s![]() ≥2s
≥2s![]()
当且仅当![]() =bv,即v=
=bv,即v=![]() 时,等号成立.
时,等号成立.
若![]() ≤c,则当v=
≤c,则当v=![]() 时,全程运输成本最小,最小值为2s
时,全程运输成本最小,最小值为2s![]() ;
;
若![]() >c,则当v∈(0,c)时,有
>c,则当v∈(0,c)时,有
s![]()
∵v∈(0,c)
∴![]() 即a>bc2 ∴a-bcv>a-bc2>0
即a>bc2 ∴a-bcv>a-bc2>0
∴s![]()
当且仅当v=c时,等号成立,即当v=c时,全程运输成本最小,最小值为s![]() .
.
综上所述,为使全程运输成本最小,当![]() ≤c时,行驶速度应为v=
≤c时,行驶速度应为v=![]() km/h;当
km/h;当![]() >c时,行驶速度为c km/h.
>c时,行驶速度为c km/h.
点评 利用平均值不等式求函数的最大值和最小值时,应注意必须具备三个条件:①都是正数;②和或积是一个常数;③这两个或三个正数可以相等.这三个条件缺一不可,本题中由v=![]() 不一定是定义域内的值,故要讨论说明.
不一定是定义域内的值,故要讨论说明.
17.解 ①∵当x是正偶数时,a<![]()
![]() +1恒成立,
+1恒成立,
∴a小于函数f (x)=![]()
![]() +1在x取正偶数时的最小值.
+1在x取正偶数时的最小值.
∵函数f (x)在x为正偶数时为增函数,
∴f (x)≥f (2)=![]() ,∴a<
,∴a<![]() .
.
②∵当x是正奇数时,a>1-![]()
![]() 恒成立,
恒成立,
∴a大于函数g(x)=-![]()
![]() +1在x取正奇数时的最大值.
+1在x取正奇数时的最大值.
∵函数g(x)在x为正奇数时为减函数,
∴g(x)≤g(1)=![]() .∴a>
.∴a>![]() .
.
综上,a∈![]() .
.
18.解 (1)∵方程f (x)-x=0的两根为x1、x2,
∴(x2-x1)2=(x2+x1)2-4x1x2=b2-2b+1-4c.
∵x2-x1>1,∴b2-2b+1-4c>1.
∴b2>2(b+2c).
(2)∵x1是方程f (x)-x=0的根,∴x1=f (x1).
∴f (t)-x1=f (t)-f (x1)=(t-x1)(t+x1+b)=(t-x1)(t+1-x2).
∵0<t<x1,∴t-x1<0.
∵x2-x1>1,∴x1+1-x2<0.
∴t+1-x2<x1+1-x2<0.故f (t)-x1>0.
(3)∵x∈[-1,1]时,恒有f (x)≤1,
∴f (0)=c≤1,f (1)=1+b+c≤1.
∴1+b=1+b+c-c≤1+b+c+-c=1+b+c+c≤1+1=2.
19.解 (1)令y=1,则f (x+1)=f (x)+f (1)+2(x+1)+1
∴f (x+1)-f (x)=2x+4
∴当x∈N*时,有f (2)-f (1)=2×1+4
f (3)-f (2)=2×2+4,f (4)-f (3)=2×3+4.
…
f (x)-f (x-1)=2(x-1)+4.
将上面各式相加得f (x)=x2+3x-3(x∈N*).
(2)当x∈N*且x≥2时,f (x)=x2+3x-3.
要使不等式f (x)≥(a+7)x-(a+10)恒成立.
即当x∈N*且x≥2时,不等式x2+3x-3≥(a+7)x-(a+10)恒成立,
即x2-4x+7≥a(x-1)恒成立
∵x≥2,∴![]() ≥a恒成立.
≥a恒成立.
又![]() =(x-1)+
=(x-1)+![]() -2≥2.
-2≥2.
(当且仅当x-1=![]() 即x=3时取“等号”)
即x=3时取“等号”)
∴![]() 的最小值是2,故a≤2.
的最小值是2,故a≤2.