高考数学复习—集合与简易逻辑试题卷
一、选择题（10×4＇=40＇）
1.设全集I={1,3,5,7,9}，集合A={1,a-5,9}， I A={5,7}，则a的值是 ( )
A.2 B.8 C.-2或8 D.2或8
2.已知集合M={xx2-x>0}, N={xx≥1}，则M∩N= ( )
A.［1,＋∞) B.(1,+∞) C. D.(-∞,0)∪(1,+∞)
3.设全集I={-2,-1,-
, 
,,1,2,3}，A={, ,1,2,3}, B={-2,2}，则集合{-2}等于 ( )
A. I A∩B B.A∩B
C. I A∩ I B D.A∪ I B
4.设集合M={x
x-m≤0}, N={g g=(x-1)2-1,x∈R}.若M∩N= ，则实数m的取值范围是 (
)
A.［-1,
B.(-1,+∞) C.(-∞,
D.(-∞,-1)
5.已知集合A={-1,2}, B={x mx+1=0},若A∪B=A，则实数m的取值范围是 ( )
A.{-1, } B.{-,1} C.{-1,0, } D.{-,0,1}
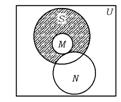6.如图，U是全集，M，N，S是U的子集，则图中阴
影部分所示的集合是 ( )
A.( U
M∩ U N)∩S B.( U(M∩N))∩S
C.( U
N∩S)∪M D.( U M∩S)∪N
7.设条件p:关于x的方程:(1-m2)x2+2mx-1=0的两根一个小
于0,一个大于1,若p是q的必要不充分条件，则条件q可
设计为 ( )
A.m∈(-1,1) B.m∈(0,1) C.m∈(-1,0) D.m∈(-2,1)
8.设两直线为l1:A1x+B1
y+C1=0, l2:A2x+B2 y+C2=0,(A2B2C2≠0)，则
是l1∥l2的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
9.如果甲是乙的必要不充分条件，乙是丙的充要条件，丙是丁的必要非充分条件，则丁是甲的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
10.关于x的方程ax2+2x+1=0至少有一个负根的充要条件是 ( )
A.0≤a≤1 B.a<1 C.a≤1 D.0<a≤1或a<0
二、填空题（4×4＇=16＇）
11.已知非空集合M满足：M
{1,2,3,4,5}且若x∈M则6-x∈M,则满足条件的集合M有 个.
12.实数a1, a2, a3,…a2004不全为0的充要条件是 .
13.关于x的不等式
>0的解集为(-3,-1)∪(2,+∞)的充要条件是
.
14.设全集S有两个子集A,B,若由x∈SA
x∈B,则x∈A是x∈SB的
条件.
三、解答题（4×11＇=44＇）
15.若A={xx=6a+8b,a,b∈Z},B={xx=2m,m∈Z},求证：A=B.
16.已知全集S={1,3,x3+3x2+2x},A={1,2x-1}，如果SA={0},则这样的实数x是否存在?若
存在，求出x，若不存在，说明理由.
17.已知条件p:A={xx2+ax+1≤0},条件q:B={xx2-3x+2≤0},若p是q的充分不必要条件，求实数a的取值范围.
18.已知p:x∈Z, y∈Z,m=x2-y2,q:k∈Z,m=2k+1或m=4k.求证:p是q的充要条件.
集合与简易逻辑参考答案
1.D (验证)若a=-2,则A={1,7,9} I
A={3,5}不合条件，若a=2,则A={1,3,9}, I
A={5,7},满足条件；若a=8则A={1,3,9}，仍符合条件，故选D.
2.B (直接计算)由x2-x>0且x≥1得x>1,故选B.
3.A (验证) I A={-2,-1,-}, I B={-1,-
,1,3}，故选A.
4.DM=(-∞,m)，N =［-1,+∞），由m<-1选D．
5.D(检验)若m=-1则B={1}不合条件，若m=0则B= 符合条件，故选D．
6.A(逐一检验)选A．
7.C 构造函数f (x)=(1-m2)x2+2mx-1, f (0)=-1,开口向上，由f (1)<0得1-m2+2m-1<0m>2或m<0.
8.C 当A2B2C2≠0时,
l1∥l2.
9.A 因丁丙乙甲，故丁甲(传递性)
10.C 若Δ=0则4-4a=0,a=1满足条件，当Δ>0时,4-4a>0a<1.综合即得.
11.(例举)M={1,5}, M={2,4}, M={3}, M={1,3,5}, M={2,3,4}, M={1,2,4,5}, M={1,2,3,4,5}7个.
12.a21+a22+a23+…+a22004≠0(偶数次幂之和不等于0).
13.a=-2(画图即知)
14.必要
15.证明：①设t∈A,则存在a、b∈Z，使得t=6a+8b=2(3a+4b)
∵3a+4b∈Z,∴t∈B即a
B.
②设t∈B,则存在m∈Z使得x=2m=6(-5m)+8(4m).
∵-5m∈Z,4m∈Z,∴x∈A即BA，由①②知A=B.
16.解：∵ S A={0},∴0∈S但0
A,∴x3+3x2+2x=0故x=0，-1,-2
当x=0时，2x-1=1, A中已有元素1，
当x=-1时，2x-1=3,3∈S;
当x=-2时，2x-1=5,但5S
故实数x的值存在，它只能是-1.
17.由条件知B=［1,2］,∵AB且A≠B,或者A=
, 故方程x2+ax+1=0无实根或者两根满足:1≤x1,x2≤2,当Δ<0时,a 2-4<0-2<a<2,当
时,a=-2，故a的取值范围是［-2,2］.
18.证明：(1)充分性:∵m=x2-y2=(x+y)(x-y)且x∈Z,y∈Z,而(x+y)与(x-y)具有相同的奇偶性.
故当x+y与x-y都为偶数时,m是4的倍数，即存在k∈Z,使m=4k;
当(x+y)与(x-y)都为奇数时,则其乘积仍为奇数，即存在k∈Z,使m=2k+1,∴pq.
(2)必要性:当m=4k时m=(k+1)2-(k-1)2，故存在整数x=k+1, y=k-1使m=x2-y2;
当m=2k+1时,则m=(k+1)2-k2=x2-y2,∴qp.