高考数学复习班第一次阶段考试试题
班级 ______姓名 ______
一．选择题：（共30分）
1．已知：
，则
是
的
（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
2．已知函数
存在反函数
，且
的图象过定点（3，1），则函数的图象一定过点 （ ）
A．
B．
C．
D．
3．已知偶函数y=f(x)在[－1，0]上为单调递减函数，又
、
为锐角三角形的两内角，则
（ ）
A．
B．
C．
D．
4．函数
定义在
上,是单调函数的充分不必要条件是
（ ）
A．
B．
C．
D．
∪
5．根据市场调查结果，预测某种家用商品从年初开始的
个月内累积的需求量
（万件）近似地满足
按此预测，在本年度内，需求量超过1.5万件的月份是
( )
（A）5月、6月 （B）6月、7月 （C）7月、8月 （D）8月、9月
6.方程
的解所在的区间是
（ ）
Ａ（０，１） Ｂ（１，２） Ｃ（２，３） Ｄ（３，４）
选择题答案栏：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 答案 |
二．填空题：（共50分）
7．已知集合
等于 。
8．过曲线
上点（1，－1）的切线方程的一般形式是 ______ 。
9．若函数
的定义域为
，则函数
的定义域为
；
10．
的值域为
；
11．设数列
的前项和为
（
）. 关于数列有下列三个命题：
（1）若既是等差数列又是等比数列，则
；
（2）若
，则是等差数列；
（3）若
，则是等比数列.
这些命题中，真命题的序号是 .
12．函数
是奇函数，当
时，
，当
时，的表达式为________________________．
13. 若方程
在区间
上有一根，则
的值为
14．已知A,B是圆O上两点,ÐAOB=2弧度,AB=2,则劣弧AB长度是________
15．函数
的单调递减区间是________________________．
16．设
，则使
为奇函数且在（0，+
）上单调递减的
值的个数为 ________________________．
三．解答题：（本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤）
17．（本小题12分）设函数
,
⑴ 求证: 不论为何实数总为增函数;
⑵ 确定的值,使为奇函数;
18．（本小题12分）已知数列{
}为等比数列，
（Ⅰ）求数列{}的通项公式；（Ⅱ）设是数列{}的前项和，证明
19．（本小题12分）已知函数
。（1）当
时，求的最大值和最小值。（2）若在
上是单调函数，且
，求
的取值范围。
20．（本小题满分14分）对函数
．
（1）若的定义域为
，值域为
，试求实数的值；
（2）若在
内是增函数，试求实数的取值范围．
21．（本小题14分）设的定义域为
，且满足
，
，有
，当
时，
。
（1）求
的值；
（2）证明在
上是增函数；
（3）解不等式
。
22．（本小题满分16分）已知二次函数
的图象过点
，且
（1）求的解析式；
（2）若数列
满足
，且
，求数列的通项公式；
（3）对于（2）中的数列，求证：①
；②
.
高考复习班第一次阶段考试数学试题答案：
| 1 | 2 | 3 | 4 | 5 | 6 |
| A | D | A | C | C | C |
7． 
8． 
9． [1,5] 10． 
11.①②③
12.
13.-2 14．
； 15．
； 16.2
17.
解: (1) 
的定义域为R, 
,
则
=
,
, 
,
即
,所以不论为何实数总为增函数.…………6分
(2) 为奇函数, 
,即
,
解得: 
………………12分
18. 解：（I）设等比数列{an}的公比为q，则a2=a1q,
a5=a1q4. 依题意，得方程组a1q=6, a1q4=162.解此方程组，得a1=2, q=3.故数列{an}的通项公式为an=2·3n－1
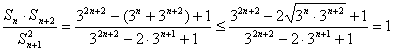
19. 解：（1）
时，
。由
，当
时，
有最小值为
，当
时，有最大值为
。
（2）
的图象的对称轴为
，由于在
上是单调函数，所以
或
，即
或
，所求的取值范围是
20. 解：设
．
（1）易知函数g(x)的值域是
，又g(x)的值域是
，∴ 3-a2=2，解得
．
（2）问题等价于函数g(x)在上为减函数，且g(x)>0对任意
恒成立，
则
且g(1)>0，解得实数a的取值范围是
。
21.解：（1）令
，则
（2）且
时，
，因为
，又当
时，，所以
，所以在上单调增。
（3）令
，则
；令
，
则
所以
，所以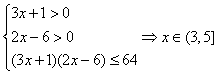
22. 解（1）由
，∴
……………………3分
解之得
即
；…………………………4分
（2）由
∴
……………………6分
由累加得
…………………………………………8分
∴
；…………………………………9分
（3）①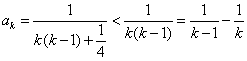
(
)
当
时，显然成立；………………………………………10分
当
时，
；……12分
②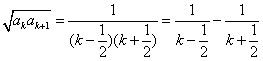
，…………………13分
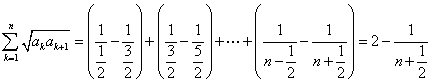，所以不等式成立
………………………16分