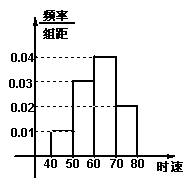高考数学总复习测试题1
班级 姓名 学号
一，选择题（5分*10=50分）
1， 
辆汽车通过某一段公路时的时速的频率分布直方
图如右图所示，时速在
的汽车大约有（ ）
.
辆
.
辆
.
辆
.80辆
2，若sin2α<0，且tanα·cosα<0，则角α在 （ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
3，已知函数
（ ）
A．是偶函数 B．是奇函数
C．不是奇函数也不是偶函数 D．有无奇偶性不能确定
4，在120个零件中，一级品24个，二级品36个，三级品60个。用系统抽样法从中抽取容量为20的样本.则每个个体被抽取到的概率是 （ ）
A． 
B．
C．
D． 
5，已知a与b均为单位向量，它们的夹角为60°，那么
等于 （ ）
A．
B．
C．
D． 4
6，若角
满足sin
+cos
=―sin―cos，则为 （ ）
A．第一象限角 B．第二象限角 C．第三象限角 D．第四象限
7，已知向量
与
的夹角为
，若向量
，且
⊥
，则
= （ ）
A．2 B．
C．
D．
8，已知向量
满足
，且
，则
与
的夹角为
（ ）
A，
B，
C，
D，
9，把函数y=cos(x+
)的图象向右平移φ个单位，所得的图象正好关于y轴对称，则
φ的最小正值为 （ ）
A. 
B. 
C.
D.
10，已知A、B、C三点不共线，O是△ABC内的一点，若
＋
＋
＝0，
则O是△ABC的 （ ）
A，内心 B，外心 C，垂心 D，重心
二，填空题（5分*6=30分）
11，若
的值是 ；
12，已知
,则
的值是 ；
13，在△ABC中，若a=2, b=2
, c=
+，则∠A的度数是
，
14，函数
的图象的对称轴方程是
．
15，
＝
．
16，函数
的单调递减区间是
；
三，解答题（10分+12分*5=70分）
17，已知函数
，
①，求其最小正周期； ②，求其最大值； ③，求其单调增区间；
18，把一颗骰子投掷两次，观察出现的点数，并记第一次出现的点数为a，第二次出现的
点数为b，向量
=（―1，－2），
①，若向量
=（―a，b），求当 ⊥ 时的慨率；
②，若向量
=（a，b），又∥, 且
=2
时,求向量的坐标;
19，设
且
在
的延长线上，使
,，则求点
的坐标
20，从10个元件中（其中4个相同的甲品牌元件和6个相同的乙品牌元件）随机选出3个参加某种性能测试. 每个甲品牌元件能通过测试的概率均为
，每个乙品牌元件能通过测试的概率均为
.试求：
（I）选出的3个元件中，至少有一个甲品牌元件的概率；
（II）若选出的三个元件均为乙品牌元件，现对它们进行性能测试，求至少有两
个乙品牌元件同时通过测试的概率.
21，设函数
，（其中
）
（Ⅰ）若f(x)的最小正周期为π，求当
时，f(x)的值域；
（Ⅱ）若函数f(x)的图象的一条对称轴方程为
，求
的值.
22，已知
（1）求
的解析式，并用
的形式表示；（6分）
（2）求方程＝1的解. （6分）
答案
一，C D B A C B C B A D
二，11，
； 12， 
； 13， 30°； 14，
；
15，
； 16，
三，
17，y=sin2x+cos2x+2=sin(2x+
)+2;
①， T=
； ②， 当x=
kπ+
(kÎZ) 时，
=
；
③， [kπ―
，kπ+] ，kÎZ
18,解: 点数对（a，b）共有6×6=36对，
①,由⊥ 得 a―2b = 0，即a =
2b，
∴数对（a，b）只有三对：（1，2）、（2，4）、（3，6），
∴向量=（―1，2）、（―2，4）、（―3，6）只有3个，
此时的慨率P =
=
;
②, =
， ∴=
=2，
+
=20，
又∥，∴b = 2 a， 得=4，点数a=2，b=4，
∴向量 =( 2 , 4 )
19, 解法一： 设分点P（x,y），∵
=―2
，l=―2
∴ (x―4,y+3)=―2(―2―x,6―y),
x―4=2x+4, y+3=2y―12, ∴ x=―8,y=15, ∴ P(―8,15)
解法二：设分点P（x,y），∵=―2， l=―2
∴ x=
=―8,
y=
=15, ∴ P(―8,15)
解法三：设分点P（x,y），∵,
∴ ―2=
, x=―8,
6=
, y=15, ∴ P(―8,15)
20, 解：（Ⅰ）事件A：选出的3个元件中，至少有一个甲品牌元件；
则P（
）=
， ∴P（A）=
1－
；
答：随机选出的3个元件中，至少有一个甲品牌元件的概率为
；
（Ⅱ）事件B：选出的三个均为乙品牌元件，至少有两个乙品牌元件通过测试
P（B）= 
=
；
答：至少有两个乙品牌元件同时通过测试的概率为；
21, 解：
（2分）
（4分）
（Ⅰ）
（6分）
（8分）
（Ⅱ）
（10分）
（12分）
22, 解：（1）
＝
＝
………………4分
＝
＝
＝
………………8分
（2）由
得 ＝1
………………9分
∴ 
(K
Z)
………10分
或
(KZ) ………………11分
所以方程的解为. {x∣
，KZ } ……12分