高中毕业班第二次适应性考试数学(理科)试题
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.
满分为150分,考试时间120分钟.
注意事项:
1. 考生将自己的姓名、准考证号及所有答案均填写在答题卡上;
2. 答题要求,见答题卡上的“填涂样例”和“注意事项”.
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1-P)n-k
球的表面积公式:S=4πR2,球的体积公式:V=![]() πR3,其中R表示球的半径.
πR3,其中R表示球的半径.
第I卷(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合P={xx(x–1)³0},Q={x![]() },则P∩Q等于
},则P∩Q等于
(A)Φ (B){x x³1} (C){x x>1} (D){x x³1或x<0}
2.如果a<0,b>0,cÎR,那么,下列不等式中正确的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.已知![]() 、
、![]() 是单位正交基向量,
是单位正交基向量,![]() ,
,![]() 。那么
。那么![]() 是
是![]() ∥
∥![]() 的
的
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D).既不充分又不必要条件
4.设![]() 是等差数列
是等差数列![]() 的前
的前![]() 项和,
项和,![]() ,则
,则![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.函数![]() 的图象的一条对称轴是
的图象的一条对称轴是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.已知(–3,1)是曲线![]() 的弦AB的中点,则弦AB所在的直线方程是
的弦AB的中点,则弦AB所在的直线方程是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
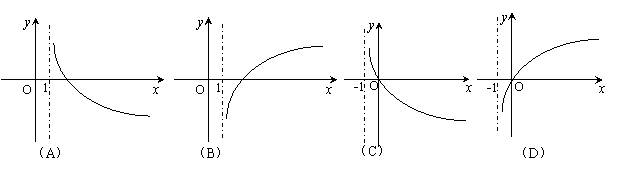 7.如果函数
7.如果函数![]() (a>0,
(a>0,![]() )是增函数,那么函数
)是增函数,那么函数![]() 的图像大致是
的图像大致是
8.五名同学进行百米赛跑比赛,先后到达终点,则甲比乙先到达的情况有
(A)240种 (B)120种 (C)60种 (D)30种
9.若![]() ,则数列的极限
,则数列的极限![]() 为
为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
10.正三棱柱![]() 的各棱长均为4,则
的各棱长均为4,则![]() 到直线
到直线![]() 的距离为
的距离为
(A)3 (B)![]() (C)
(C)![]() (D)
(D)![]()
11.点P是椭圆![]() :
:![]() 与双曲线
与双曲线![]() 的交点,
的交点,![]() 与
与![]() 是椭圆
是椭圆![]() 的焦点,则∠
的焦点,则∠![]() 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)与a的取值有关
(D)与a的取值有关
12.国际上常常用恩格尔系数来衡量一个国家和地区人民生活水平的状况。根据联合国粮农组织提出的标准,恩格尔系数在60%以上为贫困,50%~60%为温饱,40%~50%为小康,30%~40%为富裕,低于30%为最富裕。如果一个地区今年刚脱贫,以后每年食品支出和总支出分别以5%和10%的年增长率递增,如果该地区要达到富裕水平,那么大约需要
(![]() ,可参考公式
,可参考公式![]() )
)
(A)三年 (B)六年 (C)九年 (D)十二年
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分.在答题卡上的相应题目的答题区域内作答.
13.复数![]() 的虚部是
。
的虚部是
。
14.![]() 的展开式中,含
的展开式中,含![]() 项的系数为
。
项的系数为
。
15.空间三条直线中,任何两条不共面,且两两互相垂直,直线![]() 与这三条直线所成的角都为
与这三条直线所成的角都为![]() ,则
,则![]() =
。
=
。
12.已知函数![]() 在R上处处可导,当
在R上处处可导,当![]() 时,
时,![]()
![]() ,
,![]() =0。给出下列四个判断:①
=0。给出下列四个判断:①![]() ;
;
②![]() 不可能是奇函数;
不可能是奇函数;
③存在区间![]() ,使得当
,使得当![]() 时,满足
时,满足![]() ;
;
④![]() 在R上单调递增。
在R上单调递增。
判断正确的序号是 。
三、解答题:本大题共6小题,共74分,解答题应写出文字说明、证明过程或演算步骤,在答题卡上相应题目的答题区域内作答。
17、(本小题满分12分)
在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,且
,且![]() 。
。
(1)判断![]() 的形状,并加于证明;
的形状,并加于证明;
(2)当![]() 时,求
时,求![]() 面积的最大值。
面积的最大值。
18、(本小题满分12分)
甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏。已知甲每次投中的概率为![]() ,乙每次投中的概率为
,乙每次投中的概率为![]() 。求:
。求:
(1)乙投篮次数不超过1次的概率;
(2)甲、乙两人投篮次数和为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
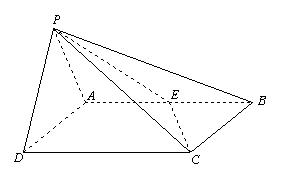 19.(本小题满分12分)
19.(本小题满分12分)
在四棱锥![]() 中,底面ABCD是矩形,AD=2,侧面PAD是正三角形且与底面ABCD垂直, E是AB中点,设PC与平面ABCD所成角为
中,底面ABCD是矩形,AD=2,侧面PAD是正三角形且与底面ABCD垂直, E是AB中点,设PC与平面ABCD所成角为![]() 。
。
(1)证明:CD⊥平面PAD;
(2)求二面角P—CE—D的大小;
(3)求点D到平面PCE的距离。
20、(本小题满分12分)
已知数列![]() 满足
满足![]() ,
,![]() 。
。
(1)求证数列![]() 是等差数列,并求
是等差数列,并求![]() 的通项公式;
的通项公式;
(2)![]() 对任何的
对任何的![]() 恒成立,求实数m取值范围。
恒成立,求实数m取值范围。
(注:n!=![]()
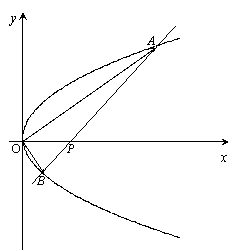
21、(本小题满分12分)
设抛物线的方程为![]() ,过点P(2,0)的直线
,过点P(2,0)的直线![]() 与抛物线交于A、B两点,点Q满足
与抛物线交于A、B两点,点Q满足![]() (lÎR)。
(lÎR)。
(1)当![]() 时,求点Q的轨迹方程;
时,求点Q的轨迹方程;
(2)若点Q在![]() 轴上,且
轴上,且![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围。
的取值范围。
22、(本小题满分14分)
已知函数![]() ,
,![]() (a¹-1),
(a¹-1),![]() 。
。
(1)若函数![]() 、
、![]() 在区间[1,2]上都为单调函数且它们的单调性相同,求实数
在区间[1,2]上都为单调函数且它们的单调性相同,求实数![]() 的取值范围;
的取值范围;
(2)a、b是函数![]() 的两个极值点,a<b,b Î(1,e] (e=2.71828…),求证:对任意的
的两个极值点,a<b,b Î(1,e] (e=2.71828…),求证:对任意的![]() 、
、![]() Î[a,b],不等式
Î[a,b],不等式![]() 成立。
成立。
高中毕业班第二次适应性考试数学(理科)试题参考答案及评分标准
说明:
一、本解答指出了每题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解答与本解答不同,可根据试题的主要内容比照评分标准制定相应的评分细则.
二、对计算题,当考生的解答 某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应给分数的一半;如果后继部分的解答有错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得的累加分数.
四、只给整数分数,选择题和填空题不给中间分.
一、选择题:本题主要考查基础知识和基本运算.
1.C 2.D 3.B 4.D 5.C 6.D
7.D 8.C 9.A 10.C 11.B 12.C
二、本大题共4个小题;每小题4分,共16分.本题主要考查基础知识和基本运算.
13.![]() 14.10 15.
14.10 15.![]() 16.②③④
16.②③④
三、解答题:
17.本题考查倍角公式和两角和与差的三角函数,及正弦定理和余弦定理等基本知识,要求学生能灵活运用所学知识解决问题.满分12分.
解:(1)法一:原式可得![]() ………………………………2分
………………………………2分
即 cosA=![]() 即 b=c×cosA
…………………………………….4分
即 b=c×cosA
…………………………………….4分
由余弦定理得: b=c×![]()
![]() c2=a2+b2,,即DABC为直角三角形
………………………………6分
c2=a2+b2,,即DABC为直角三角形
………………………………6分
法二: b=c×cosA由正弦定理得:sinB=sinC×cosA ………………………………2分
在DABC中,B=![]() –(A +C) ,
–(A +C) ,![]() sinB=sin(A+C)=sinAcosC+cosAsinC,
sinB=sin(A+C)=sinAcosC+cosAsinC,
得 sinAcosC=0 ………………………………4分
又在DABC中sinA≠0
![]() cosC=0得C=
cosC=0得C=![]()
![]() DABC为直角三角形.
………………………………6分
DABC为直角三角形.
………………………………6分
(2)法一:由(1)知DABC为直角三角形,c为斜边,
当![]() 时另两直角边长分别为sinA,cosA
………………………………8分
时另两直角边长分别为sinA,cosA
………………………………8分
![]()
![]() =
=![]() sinA cosA
sinA cosA
=![]() ×sin2A
………………………………10分
×sin2A
………………………………10分
∵AÎ(0,![]() ),
),
∴当 sin2A=1,即A=![]() 时,DABC面积的最大值为
时,DABC面积的最大值为![]() . …………………………2分
. …………………………2分
法二:由(1)知DABC为直角三角形,c为斜边,
当c=1时设另两直角边长分别为a、b,![]() ………………………………8分
………………………………8分
![]()
![]() =
=![]() ab≤
ab≤![]() (a2+b2)
=
(a2+b2)
=![]() ………………………………10分
………………………………10分
当且仅当a=b即DABC为等腰直角三角形时取等号.
![]() DABC面积的最大值为
DABC面积的最大值为![]() .
………………………………12分
.
………………………………12分
18.本题主要考查基本的概率知识及离散型随机变量分布列和数学期望等概念,以及解决实际问题的能力。满分12分。
解:记“甲投篮投中”为事件A,“乙投篮投中”为事件B。
解法一:“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中;再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,
所求的概率![]() P(
P(![]() +
+![]() ·
·![]() +
+![]() ·
·![]() ·
·![]() )
…………………………………2分
)
…………………………………2分
=P(![]() )+P(
)+P(![]() ·
·![]() )+P(
)+P(![]() ·
·![]() ·
·![]() )
)
= P(![]() )+
)+![]() ·
·![]() +
+![]() ·
·![]() ·P(
·P(![]() ) ……………………………4分
) ……………………………4分
=![]() +
+![]() +
+![]() =
=![]() .
.
答:乙投篮次数不超过1次的概率为![]() . …………………………………………5分
. …………………………………………5分
解法二:“乙投篮次数不超过1次”的对立事件是“乙投篮2次”,所以,所求的概率是
![]()
![]()
![]() ·
·![]() ·
·![]() ) …………………………………………………2分
) …………………………………………………2分
=![]() ·
·![]() ·
·![]() ……………………………………………4分
……………………………………………4分
=![]()
![]()
答:乙投篮次数不超过1次的概率为![]() . …………………………………………5分
. …………………………………………5分
(2)甲、乙投篮总次数![]() 的取值为1,2,3,4,
的取值为1,2,3,4,
![]() P(
P(![]() )=
)=![]()
![]() P(
P(![]() ·
·![]() )=
)=![]() ·
·![]() =
=![]() =
=![]()
![]() P(
P(![]() ·
·![]() ·
·![]() )=
)=![]() ·
·![]() ·P(
·P(![]() )=
)=![]() =
=![]()
![]() = P(
= P(![]() ·
·![]() ·
·![]() )=
)=![]() ·
·![]() ·
·![]() =
=![]() =
=![]() …………9分
…………9分
甲、乙投篮次数总和![]() 的分布列为
的分布列为
|
| 1 | 2 | 3 | 4 |
| P |
|
|
|
|
甲、乙投篮总次数![]() 的数学期望为
的数学期望为![]() ………11分
………11分
答:甲、乙投篮次数总和![]() 的数学期望为
的数学期望为![]() . …………………………………12分
. …………………………………12分
19.本题主要考查线面角、二面角、点面距离等知识的掌握情况,着重考查学生空间想象能力、分析问题和综合解决问题的能力.满分12分.
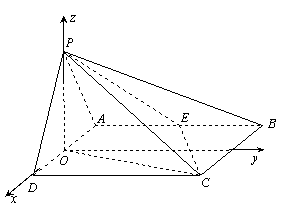 解法一:(1)证明:取AD中点O,连结OP,
解法一:(1)证明:取AD中点O,连结OP,
![]() 为等边
为等边![]() ,∴PO⊥AD,
,∴PO⊥AD,
又![]()
∴PO⊥平面ABCD,连OC,
则∠PCO为PC与面ABCD所成的角,
∴∠PCO=![]() ,AD=2,
,AD=2,
则OP=![]() ,OC=3
,OC=3
∴![]() .以O为原点,OD所在直线为x轴,过O作AB平行线为
.以O为原点,OD所在直线为x轴,过O作AB平行线为![]() 轴,OP所在直线为Z轴建立空间直角坐标系,
轴,OP所在直线为Z轴建立空间直角坐标系,
∴O(0,0,0),D(1,0,0),P(0,0,![]() ),C(1,
),C(1,![]() ,0),E(–1,
,0),E(–1,![]() ,0).
,0).
∴![]() =(1,0,0),
=(1,0,0),![]() =(0,0,
=(0,0,![]() ),
),
∴![]() =(0,
=(0,![]() ,0)×(1,0,0)=0,
,0)×(1,0,0)=0,
![]() =(0,
=(0,![]() ,0)×(0,0,
,0)×(0,0,![]() )=0, ………………………………3分
)=0, ………………………………3分
∴![]() ,
,![]() ,又OD∩OP=O,∴CD⊥平面ODP. ……………………4分
,又OD∩OP=O,∴CD⊥平面ODP. ……………………4分
(2)由(1)得![]() =(–1,
=(–1,![]() ,
,![]() ),
),![]() =(1,
=(1,![]() ,
,![]() ),
),
设平面PCE的一个法向量为![]() =(x,y,z)
=(x,y,z)
则 ,即
,即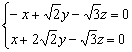 ,取x=1,得
,取x=1,得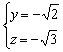 , ………………7分
, ………………7分
∴平面PCE的一个法向量![]() =(1,
=(1,![]() ,
,![]() ),
),
又易知平面DEC的一个法向量为![]() =(0,0,
=(0,0,![]() ),
),
∴![]() ………………………………8分
………………………………8分
![]() 二面角P—CE—D的平面角大小为
二面角P—CE—D的平面角大小为![]() .
………………………………9分
.
………………………………9分
(3)解:∵![]() =(0,
=(0,![]() ,0),平面PCE的一个法向量为
,0),平面PCE的一个法向量为 ![]() =(1,
=(1,![]() ,
,![]() )
)
设D到面PEC的距离为d, 则![]() ……………………10分
……………………10分
解法二:(1)![]() 面ABCD为矩形,∴CD⊥AD,
面ABCD为矩形,∴CD⊥AD,
又,面![]() 面ABCD,∴CD⊥平面ABCD
………………………………4分
面ABCD,∴CD⊥平面ABCD
………………………………4分
(2)取AD的中点O,连结OP,OC ,OE,
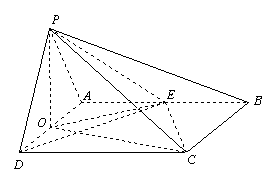 ∵DPAD为等边D,∴OP⊥AD,
∵DPAD为等边D,∴OP⊥AD,
又面![]() 面ABCD,∴PO⊥平面ABCD,
面ABCD,∴PO⊥平面ABCD,
则∠PCO为PC与面ABCD所成的平面角,
∴![]() ………………5分
………………5分
∵AD=2,在等边![]() PAD 中OP=
PAD 中OP=![]() ,DOPC中,OC=3 ,∴
,DOPC中,OC=3 ,∴![]() ,
,
∵E为AB中点,∴AE=![]() ,∴在RtDAOE中,OE=
,∴在RtDAOE中,OE=![]() ,同理,CE=
,同理,CE=![]() ,
,
由![]() ,
,
得∠OEC=![]() ………………………………7分
………………………………7分
又OP⊥平面ABCD,∴PE⊥CE.
∴∠PEO是二面角P—CE—D的平面角,
∴![]() ,∴∠PEO=
,∴∠PEO=![]() .
………………………………9分
.
………………………………9分
(3)由(2)知DPEC为RtD,连接DE,
∴![]()
![]()
![]() ,设D到平面DEC的距离为d
………………………………11分
,设D到平面DEC的距离为d
………………………………11分
∴![]() ,∴
,∴![]() =
=![]() . ………………………12分
. ………………………12分
20.本题主要考查递推数列和等差数列的概念,将求和问题迁移为求积问题,考查类比思想.满分12分.
证明:(1)![]()
![]() ,
……………………2分
,
……………………2分
所以![]() 是以
是以![]() 为首项,1为公差的等差数列,
为首项,1为公差的等差数列,
所以![]() ,即
,即![]() ………………………………4分
………………………………4分
(2)![]() ………………………………6分
………………………………6分
![]() 时,
时,![]()
![]()
……………………………………8分
而n=1时,![]() ,n=2时,
,n=2时,![]() 也满足上式
……………………10分
也满足上式
……………………10分
所以![]() <m对任何
<m对任何![]() 恒成立,只需
恒成立,只需![]()
所以当![]() 时,
时,![]() 对任何的
对任何的![]() 恒成立.…………………12分
恒成立.…………………12分
 21.本题考查解析几何的基本思想和方法,要求考生能正确分析问题,寻找较好的入题方向,同时兼顾考查算理和逻辑推理的能力,要求对代数式合理演变,以便于求参数范围.满分12分。
21.本题考查解析几何的基本思想和方法,要求考生能正确分析问题,寻找较好的入题方向,同时兼顾考查算理和逻辑推理的能力,要求对代数式合理演变,以便于求参数范围.满分12分。
解法一:设直线![]() 的方程为
的方程为![]() ,代入
,代入![]() 得:
得:![]() ,
,
设A、B点的坐标分别为![]() 、
、![]()
则![]() ,
,![]() ,……2分
,……2分
(1)设![]() ,
,![]()
![]()
![]()
![]() …4分
…4分
消去m得:![]() 即点
即点![]() 的轨迹方程为:
的轨迹方程为:![]() ………………………6分
………………………6分
(2)![]() 且点
且点![]() 在
在![]() 轴上。
轴上。
![]() 即
即![]() …………………………………8分
…………………………………8分
![]() 消去
消去![]() 得:
得:![]()
![]() …………………………………10分
…………………………………10分
设![]() 当
当![]() 时,
时,![]() 恒成立。
恒成立。
![]() 即
即![]() ,又
,又![]()
![]()
![]() 或
或![]() 即为直线
即为直线![]() 的斜率
的斜率![]() 的取值范围. ……………………12分
的取值范围. ……………………12分
解法二:(1)![]() 当直线
当直线![]() 的斜率不存在时,由抛物线的对称性
的斜率不存在时,由抛物线的对称性
得Q点坐标为(4,0) ……………………1分
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() 代入
代入![]() 得:
得:
![]()
![]()
设A、B、Q点的坐标分别为![]() 、
、![]() 、
、 ![]() ………………2分
………………2分
![]() ,
, ,
,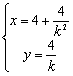 ………4分
………4分
消去k得:![]() ,又点(4,0)的坐标也在满足方程,
,又点(4,0)的坐标也在满足方程,
![]() 点
点![]() 的轨迹方程为:
的轨迹方程为:![]() …………………………6分
…………………………6分
(2)![]() 且点
且点![]() 在
在![]() 轴上,
轴上,
![]() 即
即![]()
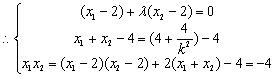 ………………………………8分
………………………………8分
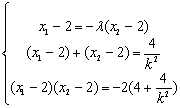 整理得:
整理得:![]() ……………10分
……………10分
设![]() ,当
,当![]() 时,
时,![]() 恒成立
恒成立
![]()
![]()
![]() 。
。
![]() 或
或![]() 即为直线
即为直线![]() 的斜率
的斜率![]() 的取值范围. …………………………12分
的取值范围. …………………………12分
(1)解法三:设A、B点的坐标分别为![]() 、
、![]()
![]()
![]() 两式相减得:
两式相减得:![]() …………2分
…………2分
设![]()
![]()
![]() 且
且![]() …………………………4分
…………………………4分
 ……………………………………5分
……………………………………5分
即点![]() 的轨迹方程为:
的轨迹方程为:![]() …………………………6分
…………………………6分
22.本题主要考查导数和方程、不等式的基本知识,要求学生能利用导数的方法解决函数的单调性和最值问题,寻找合理的途径,构造函数的方法证明不等式.满分14分.
解::(1)![]() ,
…………………………2分
,
…………………………2分
![]() ,
,
∵![]() 在区间[1,2]上都为单调函数且它们的单调性相同,
在区间[1,2]上都为单调函数且它们的单调性相同,
∴![]() ,∵
,∵![]() ,∴
,∴![]() ,…………4分
,…………4分
∵![]() ∴
∴![]() 或
或![]() (
(![]() ),又
),又![]() ,
,
∴![]() 或
或![]() .
……………………………6分
.
……………………………6分
(2)∵![]() 或
或![]() ,
,
又∵![]() 有两不等正根
有两不等正根![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
………………………………8分
,
………………………………8分
∴当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
则对任意的![]() ,
,
![]()
=![]() ,
……………………10分
,
……………………10分
设![]() ,则
,则![]() ,
,
∵当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递增,……………………12分
单调递增,……………………12分
∴![]() ,∴
,∴![]() 也在
也在![]() 单调递增,
单调递增,
∴![]() ,
,
∴不等式![]() 对任意的
对任意的![]() 成立.
………………14分
成立.
………………14分