高中毕业班质量检查数学（文科）试题
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题），全卷满分150分，考试时间120分钟.
注意事项：
1．考生将自己的姓名、准考证号及所有答案均填写在答题卡上。
2．答题要求，见答题卡上的“填涂样例”和“注意事项”。
参考公式：
如果事件A、B互斥，那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立，那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P，那么n次独立重复试验中恰好发生k次的概率
球的表面积公式 
，其中R表示球的半径
球的体积公式 
，其中R表示球的半径
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的，在答题卡上相应题目答题区域内作答.
1．若全集U={1，3，5，7}，A={1，3，7}，B={3，5}，则
为 （ ）
A．{1，3，5} B．{3，5，7} C．{5，7} D．{1，5，7}
2．已知：l1、l2是空间两条直线，条件p：l1、l2没有公共点；条件q：直线l1、l2是平行直线.
则是p是q的 （ ）
A．充分不必要条件 B．必要不充分
C．充要条件 D．既非充分又非必要条件
3．M为曲线
上的任意一点，在点M处的切线的叙率为k，则k的取值范围是
（ ）
A．
B．（1，+∞） C．
D．
4．定义在R上的函数
，则f(x)可以是（ ）
A．
B．
C．
D．
5．已知函数
的反函数y=f－1(x)图象过一个定点，那么这个
定点的坐标是 （ ）
A．（0，－3） B．（－3，1） C．（－2，2） D．（0，－2）
6．已知F1、F2是双曲线
的两个焦点，M为双曲线上的点，若
MF1⊥MF2，∠MF2F1 = 60°，则双曲线的离心率为 （ ）
A．
B．
C．
D．
7．若
的展形式中x2的系数
，则n的值 （ ）
|
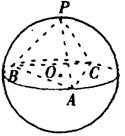
8．如图，正三棱锥P—ABC内接于球O，球
心O在底面ABC上，且AB=
，则球的
表面积为（ ）
A．π B．2π
C．4π D．9π
9．在△ABC中，a=8，B=75°，C=60°，则c边长为 （ ）
A．8（－1） B．4
C．4 D．4
|
A．arctan
B．arctan
C．arctan3 D．arctan
11．在某次植树活动中，某学校将高二年段的四名教师分配到A、B、C、D四个不同的植树点开展活动，每个植树点安排1人.由于工作需要，甲不能到A植树点，乙不能到C植树点，那么不同的分配方案有 （ ）
A．12种 B．14种 C．18种 D．20种
12．已知函数
，若实数x0是方程f(x)=0的解，且0<x1<x0，则f(x1)的值
（ ）
A． 恒为正值 B．等于0 C．恒为负值 D．不大于0
|
二、填空题：本大题共4小题，每小题4分，共16分，在答题卡上的相应题目的答题区域内作答.
13．不等式
的解集为
；
14．设i，j是平面直角坐标系分别与x轴、y轴正方向相同的两个单位向量，已知a=3i－j，
b=mi+2j（m为实数），且a⊥b，则b= ；
|
16．直线
相切，其中m、
，试写出所有满足条件的有序实数对(m，n)：
.
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤，在答题卡上相应题目的答案区域内作答.
17．（本小题满分12分）
已知α为直线x+3y=0的倾斜角.
（1）求
的值；
（2）求
的值.
18．（本小题满分12分）
已知等差数列{an}中，a1=－2，a2=1.
（1）求{an}的通项公式；
（2）调整数列{an}的前三项a1、a2、a3的顺序，使它成为等比数列{bn}的前三项，求{bn}的前n项和.
19．（本小题满分12分）
为丰富学生的课余生活，学校决定在高一年段开设系列选修课，并开放了三间多媒体教室，且各门选修课是否使用多媒体教室互不影响.
（1）若周一下午开设的A、B、C三门选修课使用多
媒体教室的概率分别为
求这三门选修课中恰有
二门课使用多媒体教室的概率；
（2）若周二下午开设的五门选修课使用多媒体教
|
，求多媒体教室不够使用的概率.
20．（本小题满分12分）
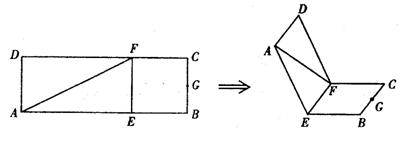
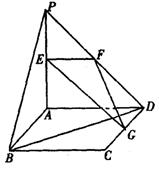
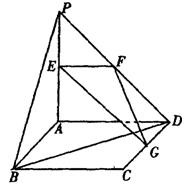
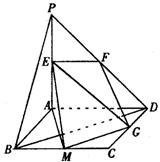
如图，平面PAD⊥平面ABCD，ABCD为正方形，
△PAD是直角三角形，且PA=AD=2，E、F、G分别是
线段PA、PD、CD的中点.
（1）求证：EFG⊥面PAB；
（2）求异面直线EG与BD所成的角；
|
21．（本小题满分12分）
已知a∈R，函数
（1）如果函数
是偶函数，求f(x)的极大值和极小值；
（2）如果函数f(x)是（－∞，+∞）上的单调函数，求a的取值范围.
22．（本小题满分14分）
|
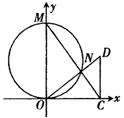
（1）若点N（，1），求点D的坐标；
（2）若点N沿着圆周运动，求点D的轨迹E的方程；
（3）设P（0，a）（a>0），Q是点P关于原点的
对称点，直线l过点P交曲线E于A、B两
点，点H在射线QB上，且AH⊥PQ，求证：
不论l绕点P怎样转动，恒有 
.
高中毕业班质量检查数学（文科）试题参考答案
说明：
一、本解答指出了每题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制定相应的评分细则。
二、对计算题，当考生的解答在某一步出现错误时，如果后断部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答给分数的一半；如果后继部分的解答在较严重的错误，就不再给分。
三、解答右端所注分数，表示考生正确做到这一步应得的累加分数.
四、只给整数分数。选择题和填空题不给中间分。
一、选择题：本题考查基础知识和基本运算，每小题5分，满分60分。
1.D 2.B 3.C 4.D 5.B 6.C 7.C 8.C 9.B 10.A 11.B 12.A
|
13.（－1，0） 14.
15.
16.（1，1），（2，2），（3，4），（4，8）（填对一组即可）
三、解答题：
17．本小题主要考查直线倾斜角的概念、两角和与差的三角函数、倍角公式等基础知识和基
本运算能力.满分12分.
解：依题意，得
.…………………………………………2分
（1）
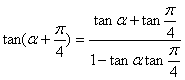……………………………………4分
（2）
………………………………9分
18．本小题主要考查等差数列、等比数列的基础知识，以及基本运算技能.满分12分.
解：（1）由已知，得a2－a1=1－(－2)=3
∴{an}的公差d=3…………………………………………………………2分
∴an=a1+(n－1)d=－2+3(n－1)
=3n－5………………………………………………………………4分
（2）由（1），得a3=a2+d=1+3=4，∴a1=－2，a2=1，a3=4.
依题意可得：数列{bn}的前三项为b1=1，b2=－2，b3=4或b1==4，b2=－2，b3=1
（i）当数列{bn}的前三项为b1=1，b2=－2，b3=4时，则q=－2………………6分
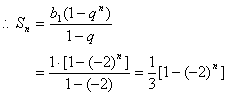………………………………8分
（ii）当数列{bn}的前三项为b1=4，b2=－2，b3=1时，则
.………………………………………………………………10分
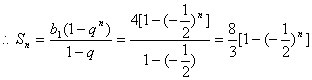…………………12分
19．本小题主要考查互斥事件、相互独立事件及n次独立重复试验事件A发生k次的概率等基础知识和运算能力，以及运用概率的知识分析和解决问题的能力.满分12分.
解：（1）记A、B、C三门选修课使用多媒体教室为事件A、B、C，恰好有二门选修课使用多媒体教室可以分成A·B·
、A·
·C、
·B·C，………………2分
根据互斥事件和相互独立事件的概率公式，
得
；……5分
答：恰有二门选修课使用多媒体教室的概率为
……………………6分
（2）记某选修课需要使用多媒体教室为事件D，多媒体教室不够使用，表明至少有四门选修课需要使用多媒体教室，由于各门选修课之间是否使用多媒体教室互不影响，问题转化为五次独立复试验中事件D至少发生4次……………………7分
∵恰有4门选修课需要使用多媒体教室的概率为
恰有5门选修课需要使用多媒体教室的概率为
故
………………………………………………11分
答：多媒体教室不够使用的概率为
………………………………12分
20．本小题主要考查面面关系，两异面直线所成的角以及点到平面距离等基础知识，考查空间想象能力，逻辑思维能力和运算能力。满分12分。
|
（1）证明：∵ABCD为正方形，△PAD是直角三角形，
且PA=AD=2，
∴AD⊥AB，AD⊥PA
又AB∩PA=A，
∴AD⊥面PAB.………………1分
∵E、F分别是线段PA、PD的中点，
∴EF/AD，
∴EF⊥面PAB.…………………………2分
又EF
面EFG，
∴面EFG⊥面PAB.……………………3分
（2）解：取BC的中点M，连结GM、AM、EM，则GM//BD，
|
所成的角.………………4分
在Rt△MAE中， 
，
同理
，…………………………5分
又
，
∴在△MGE中，
………………6分
故异面直线EG与BD所成的角为arccos
，………………………………7分
|
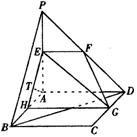
∴E、F、G、H四点共面，过点A作AT⊥HE于T，
∵面EFGH⊥面PAB，∴AT⊥平面EFGH，……9分
∴AT就是点A到平面EFG的距离.……10分
在Rt△AEH中，AE=AH=1，
∴
，
故点A到平面EFG的距离为
.……………………12分
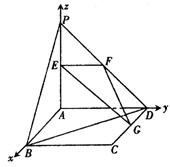
解法二：建立如图所示的空间直角坐标系A－xyz，
则A（0，0，0），B（2，0，0），C（2，2，0），D（0，2，0），
|
（1）证明：∵
=（0，1，0），
=（0，0，2），
=（2，0，0），
∴·=0×0+1×0+0×2=0，
·=0×2+1×0+0×0=0，
∴EF⊥AP，EF⊥AB.………………………………………………1分
又∵AP、AB面PAB，且PA∩AB=A，
∴EF⊥平面PAB.………………………………………………2分
又EF面EFG，
∴平面EFG⊥平面PAB.…………………………………………3分
（2）解：∵
,…………………………4分
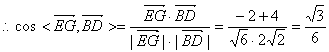，………………6分
故异面直线EG与BD所成的角为arcos.…………………………7分
（3）解：设平面EFC的法向量
=（x,y,z），……………………………………8分
则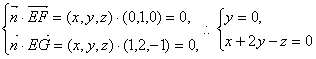
………………10分
令z=0，得=（1，0，1）.……………………………………11分
又
=（0，0，1），
∴点A到平现EFG的距离
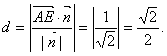……………………………………12分
21．本题主要考查导数、函数奇偶性、单调性、极值等知识和分类讨论思想，检测综合运用数学知识解决问题的能力.满分12分.
解：
……………………………………1分
（1）∵f′(x) 是偶函数，∴a=－1.…………………………………………2分
此时
解
，由
| x | (－∞,－2 | －2 | (－2 | 2 | (2 |
| f′(x) | + | 0 | － | 0 | + |
| f(x) |
| 极大值 |
| 极小值 |
|
可知：f(x)的极大值为f(－2)=4, f(x)的极小值为f(2)=－4.……6分
（2）当
恒有
>0.
∴0<a<2时，f(x)的(－∞，+∞)上为单调递增函数.……………………9分
当△=0时，a=0或a=2，
若
∴函数y= f(x)在（－∞，+∞）上为单调递增函数.……………………10分
若
∴函数y= f(x)在（－∞，+∞）上为单调递增函数.……………………11分
当△>0时，a<0或a>2，=0有两个不等实根x1、x2，不妨设x1<x2，此时
f(x)在（－∞，x1）及（x2，+∞）为增函数，在（x1，x2）为减函数，不符合要求.
综上，如果函数f(x)是（－∞，+∞）上的单调函数，a的取值范围是{a0≤a≤2}.
…………………………………………………………12分
22．本小题主要考查直线、圆、抛物线等基础知识，考查解析几何的基本思想和方法，考查综合应用知识分析问题和解决问题能力.满分14分.
解：（1）∵M（0，4）、N（，1），
∴MN所在直线方程为
……………………1分
令
…………………………………………2分
又ON所在直线方程为y=
x，
由
.
|
.……………………………………3分
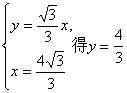（2）方法一：M（0，4），O（0，0），设D（x,y）N（x1，y1）
∴C（x，0）.
过N作NK⊥OC于K，则NK//CD//OM，………………4分
， ①………………5分
，② ……………………6分
由①②得：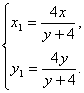
……………………………………7分
∵点N在圆
，
即
整理得：x2=4y.……………………………………………………8分
方法二：设D（x,y），∠DOC=α，∴∠CMO=∠DOC=α.………………4分
x=±OC=±OM·tanα=±4tanα，…………………………………………6分
y=OCtanα=OMtan2α=4tan2α，…………………………………………7分
消去α得：x2=4y.………………………………………………………………8分
方法三：设N（x1，y1）D（x，y）则C（x，0）.
∵M、N、C共线，
又∵O、N、D共线，
……………………………………4分
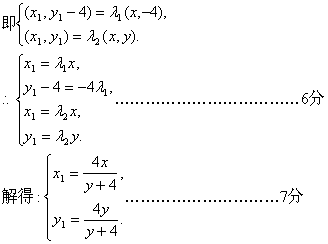
∵点N在圆，
即
整理得：x2=4y.……………………………………………………8分
（3）∵直线l过点P（0，a）且交曲线x2=4y于A、B两点，故可设直线l的方程为y=kx+a
A（x1，y1），B（x2，y2）.
由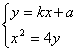
得
，
∴x1x2=－4a.…………………………9分
设P分的比为λ，则
，
且
………………………………10分
又
.
∵点H的射线QB上，设
，则
……11分
…………………………………………12分
即：
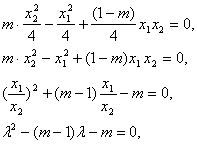
…………………………13分
依题意，得λ>0，m>0，
……………………14分