高中总复习数学高考热点问题训练
一、选择题
1.如图所示是2008年北京奥运会的会徽,其中的“中国印”由四个色块构成,可以用线段在不穿越其他色块的条件下将其中任意两个色块连接起来(如同架桥),如果用三条线段将这四个色块连接起来,不同的连接方法共有( )

A.8种 B.12种 C.16种 D.20种
2.某文艺团体下基层进行宣传演出,原准备的节目表中有6个节目,如果保持这些节目的相对顺序不变,在它们之间再插入2个小品节目,并且这2个小品节目在节目表中既不排头,也不排尾,则不同的插入方法有( )
A.20种 B.30种 C.42种 D.56种
3.禽养殖业成了我国一些地区发展农村经济的一个新举措.下列两图是某县2000~2005年家禽养殖业发展规模的统计结果,那么,此县家禽养殖数最多的年份是 …( )


A.2000年 B.2001年 C.2003年 D.2004年
4.定义运算![]() =ad-bc,则符合条件
=ad-bc,则符合条件![]() =0的点P(x,y)的轨迹方程为( )
=0的点P(x,y)的轨迹方程为( )
A.(x-1)2+4y2=1 B.(x-1)2-4y2=1
C.(x-1)2+y2=1 D.(x-1)2-y2=1
5.(理)已知f(x)=2+x2cos(![]() +x)在[-a,a](a>0)上的最大值与最小值分别为M、m,则M+m的值为( )
+x)在[-a,a](a>0)上的最大值与最小值分别为M、m,则M+m的值为( )
A.0 B.2 C.4 D.与a的取值有关
(文)(2006浙江杭州二中模拟,文4)函数f(x)=![]() x3+ax+1在(-∞,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
x3+ax+1在(-∞,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
A![]() B.1
C.
B.1
C.![]() D.-1
D.-1
6.(理)若函数y=(![]() ) 1-x+m的图象与x轴有公共点,则m的取值范围是… ( )
) 1-x+m的图象与x轴有公共点,则m的取值范围是… ( )
A.m≤-1 B.-1≤m<0 C.m≥1 D.0<m≤1
(文)设函数f(x)=![]() 则
则![]() (a≠b)的值为
(a≠b)的值为
( )
A.a B.b C.a,b中较小的数 D.a,b中较大的数
7.设A、B是非空集合,定义A×B={xx∈A∪B,且x![]() A∩B},已知A={xy=2x-x2,
A∩B},已知A={xy=2x-x2, ![]() },B={yy=
},B={yy=![]() (x>0)},则A×B等于( )
(x>0)},则A×B等于( )
A.[0,1]∪(2,+∞)B.[0,1)∪(2,+∞)
C.[0,1]D.[0,2]
8.若动点(x,y)在曲线![]() =1(b>0)上变化,则x2+2y的最大值为( )
=1(b>0)上变化,则x2+2y的最大值为( )
A. B
B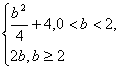
C.![]() D.2b
D.2b
9.已知k<-4,则函数y=cos2x+k(cosx-1)的最小值是( )
A.1 B.-1 C.2k+1 D.-2k+1
10.已知函数f(x)满足2f(x)-![]() =f(
=f(![]() ),则f(x)的最小值是( )
),则f(x)的最小值是( )
A.![]() B.2
C.
B.2
C.![]() D.
D.![]()
二、填空题
11.(理)一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=6,则在第7组中抽取的号码是_________.
(文)一个公司共有280个员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为40的样本,如果从某个部门的所有员工抽取的员工人数是5,那么这个部门的员工人数为_____________.
12.2005年10月,我国载人航天飞船“神六”飞行获得圆满成功.已知“神六”飞船变轨前的运行轨道是一个以地心为焦点的椭圆,飞船近地点、远地点离地面的距离分别为200公里、250公里.设地球半径为R公里,则此时飞船轨道的离心率为_________.(结果用R的式子表示)
13.把实数a,b,c,d排形成如![]() 的形式,称之为二行二列矩阵.定义矩阵的一种运算
的形式,称之为二行二列矩阵.定义矩阵的一种运算![]() ·
·![]() ,该运算的几何意义为平面上的点(x,y)在矩阵
,该运算的几何意义为平面上的点(x,y)在矩阵![]() 的作用下变换成点(ax+by,cx+dy),则点(2,3)在矩阵
的作用下变换成点(ax+by,cx+dy),则点(2,3)在矩阵![]() 的作用下变换成点_________.又若曲线x2+4xy+2y2=1在矩阵
的作用下变换成点_________.又若曲线x2+4xy+2y2=1在矩阵![]() 的作用下变换成曲线x2-2y2=1,则a+b的值为____________.
的作用下变换成曲线x2-2y2=1,则a+b的值为____________.
14.在△ABC中,O为中线AM上的一个动点,若AM=2,则![]() (
(![]() )的最小值是_________.
)的最小值是_________.
三、解答题
15.甲、乙、丙三个口袋内都分别装有6个不相同的球,并且每个口袋内的6个球均有1个红球,2个黑球,3个无色透明的球,现从甲、乙、丙三个口袋中依次随机各摸出1个球.
理科:(1)求恰好摸出红球、黑球和无色球各
1个的概率;
(2)求摸出的3个球中含有有色球数ξ的概率分布列和数学期望.
文科:(1)求恰好摸出2个黑球的概率;
(2)求恰好摸出红球、黑球和无色透明球各1个的概率;
(3)求摸出的3个球中至少有1个是有色球的概率.
16.某公司为了帮助尚有26.8万元无息贷款没有偿还的残疾人商店,借出20万元将该商店改建成经营状况良好的某种消费品专卖店,并约定用该店经营的利润逐步偿还债务(不计息).已知:该种消费品的进价为每件40元;该店每月销售量q(百件)与销售价p(元/件)的关系用图中的一条折线表示;职工每人每月工资为600元,该店应交付的其他费用为每月13 200元.
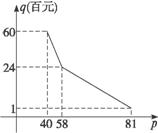
(1)如果当销售价p为52元/件时,该店正好收支平衡,求该店的职工人数;
(2)如果该店只安排40名职工,则该店最早可在几年后还清所有债务,此时每件消费品价定为多少元?
17.某花木场存放装满泥土的花盆,每堆最底层(第一层)摆放呈长20只,宽14只的矩形,上面各层均比它的下一层长宽各少一只.已知每只装满泥土的花盆的重量为2kg,为使堆放稳定,每两层之间放有一块耐压的轻质薄板(重量忽略不计).每只花盆的最大抗压力为8kg,所有花盆不破碎、不变形
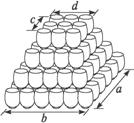 .
.
(1)求第n层(自下而上,下同)摆放多少只花盆?
(2)问这堆花盆能否摆7层?如果能,求出第7层的花盆数;如果不能,说明理由,并求这堆花盆最多可摆多少只.
18.已知函数y=f(x)满足f(x)=![]()
(1)分别写出x∈[0,1)时y=f(x)的解析式f1(x)和x∈[1,2)时y=f(x)的解析式f2(x);并猜想x∈[n,n+1],n≥-1,n∈Z时y=f(x)的解析式f n+1(x)(用x和n表示)(不必证明);
(2)当x=n+![]() (n≥-1,n∈Z)时,y=f n+1(x)x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列A n+1(x,f(x))和点列B n+1(n+1,f(n+1)),线段A n+1B n+2与线段B n+1A n+2的交点C n+1,求点C n+1的坐标(a n+1(x),b
n+1(x));
(n≥-1,n∈Z)时,y=f n+1(x)x∈[n,n+1),(n≥-1,n∈Z)的图象上有点列A n+1(x,f(x))和点列B n+1(n+1,f(n+1)),线段A n+1B n+2与线段B n+1A n+2的交点C n+1,求点C n+1的坐标(a n+1(x),b
n+1(x));
(3)在前面(1)(2)的基础上,请你提出一个点列C n+1(a n+1(x),b n+1(x))的问题,并进行研究,并写下你研究的过程.
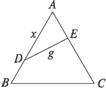
19.如图,公园有一块边长为2a的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(1)设AD=x(x≥0),ED=y,求用x表示y的函数关系式;
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请予证明.
20.已知函数f(x)的定义域为[0,1],且同时满足:①f(1)=3;②f(x)≥2恒成立;③若x1≥0,x2≥0,x1+x2≤1,则有f(x1+x2)≥f(x1)+f(x2)-2.
(1)试求函数f(x)的最大值和最小值;
(2)试比较f(![]() n)与
n)与![]() n+2的大小(n∈N);
n+2的大小(n∈N);
(3)某人发现:当x=![]() n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
n(n∈N)时,有f(x)<2x+2.由此他提出猜想:对一切x∈(0,1],都有f(x)<2x+2,请你判断此猜想是否正确,并说明理由.
高中总复习数学高考热点问题训练参考答案
一、选择题
1. C
解析:四个点取两个点,可以组成![]() =6条线段,6条线段又可以得到
=6条线段,6条线段又可以得到![]() 个三角形,但有四个三角形不符合条件,故不同的连接方法共有
个三角形,但有四个三角形不符合条件,故不同的连接方法共有![]() -4=16种.
-4=16种.
2. B
解析:原6个节目中间有5个空挡,插入2个小品节目不相邻有![]() =20种不同的插入方法;插入2个小品节目相邻有
=20种不同的插入方法;插入2个小品节目相邻有![]() =10种不同的插入方法,故共有20+10=30种不同的插入方法.
=10种不同的插入方法,故共有20+10=30种不同的插入方法.
3. B
解析:2000养殖数为30×1=30万只;2001年养殖数为26×1.2=31.2万只;
2003年养殖数为18×1.6=28.8万只;2004年养殖数为14×1.8=25.2万只.
4. A
解析:![]() =0
=0![]() (x-1)2-(1-2y)(1+2y)=0,即(x-1)2+4y2=1.
(x-1)2-(1-2y)(1+2y)=0,即(x-1)2+4y2=1.
5.(理)C
解析:f(x)=2-x2sinx,令g(x)=-x2sinx,则g(x)是[-a,a]上的奇函数,所以g(x) min+g(x) max=0,M=g(x)max+2,N=g(x) min+2,所以M+N=4.
(文)C
解析:∵![]() ,又
,又![]() ,∴a= -1,f(1)=
,∴a= -1,f(1)= ![]() -1+1=
-1+1=![]() .
.
6.(理)B
解析:∵1-x≥0,∴y=(![]() ) 1-x∈(0,1),若函数y=(
) 1-x∈(0,1),若函数y=(![]() ) 1-x+m的图象与x轴有公共点,
) 1-x+m的图象与x轴有公共点,
则![]()
(文)C
解析:当a>b时,![]() =b;
=b;
当a<b时,![]() =
=![]() =a.故选C.
=a.故选C.
7.A
解析: ∵A={x0≤x≤2},B={yy= ![]() (x>0)}={yy>1},
(x>0)}={yy>1},
∴A∪B={xx≥0},A∩B={x1<x≤2},A×B=[0,1]∪(2,+∞).
8. A
解析:f(y)=x2+2y=4-![]() +2y=
+2y=![]() (y
(y![]() )2+
)2+![]() +4,又因-b≤y≤b,
+4,又因-b≤y≤b,
∴当![]() <b即0<b<4时,f(y) max=
<b即0<b<4时,f(y) max=![]() +4;当
+4;当![]() ≥b即b≥4时,f(y)递增,f(y) max=f(b)=2b.
≥b即b≥4时,f(y)递增,f(y) max=f(b)=2b.
9. A
解析:∵y=2cos2x+kcosx-k-1=2(cosx+![]() )2-
)2-![]() -k-1,又k<-4,-1≤cosx≤1,∴当cosx=1时,y取最小值,最小值为2×12+k×1-k-1=1.
-k-1,又k<-4,-1≤cosx≤1,∴当cosx=1时,y取最小值,最小值为2×12+k×1-k-1=1.
10. C
解析: ∵2f(x)- ![]() =f(
=f(![]() )2f(
)2f(![]() )-x=f(x),
)-x=f(x),
∴f(x)=![]() (x+
(x+![]() )≥
)≥![]() ,等号当且仅当x=
,等号当且仅当x=![]() 时成立.
时成立.
二、填空题
11.(理) 62
解析:在第7组中抽取的号码是第三个,即为62.
(文) 35
解析:![]() =35.
=35.
12. ![]()
解析:![]()
13. (3,2) 2
解析:(ax+by,cx+dy)=(0×2+1×3,1×2+0×3)=(3,2),
设(x,y)是曲线x2+4xy+2y2=1的点,在矩阵![]() 的作用下的点为(x′,y′),即
的作用下的点为(x′,y′),即![]() 又x′2-2y′2=1,∴(x+ay)2-2(bx+y)2=1,(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1.
又x′2-2y′2=1,∴(x+ay)2-2(bx+y)2=1,(1-2b2)x2+(2a-4b)xy+(a2-2)y2=1.
故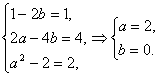 ∴a+b=2.
∴a+b=2.
14. -2
解析:![]() ·(
·(![]() )=
)=![]() ·
·![]() =
=![]() ≥-2 =-2.
≥-2 =-2.
当O为AM的中点时等号成立.
三、解答题
15.由于各个袋中球的情况一样,而且从每一个袋中摸出红球、黑球、无色球的概率均分别为![]() ,
,![]() ,
,![]() ,所以根据相互独立事件同时发生的概率公式可得.
,所以根据相互独立事件同时发生的概率公式可得.
理科:(1)P=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() .
.
(2)ξ的取值为0,1,2,3,并且
P(ξ=0)=(![]() )3=
)3=![]() ;P(ξ=1)=
;P(ξ=1)=![]() (
(![]() +
+![]() )(
)(![]() )2=
)2=![]() ;
;
P(ξ=2)=![]() (
(![]() +
+![]() )2(
)2(![]() )=
)=![]() ;P(ξ=3)=
;P(ξ=3)=![]() (
(![]() +
+![]() )3=
)3=![]() .
.
从而ξ的概率分布列为
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
并且Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.
文科:(1)P=![]() (
(![]() )2(1-
)2(1-![]() )=
)=![]() ;
;
(2)P=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() .
.
(3)P=1-(![]() )3=
)3=![]()
16.(1)设该店每月的利润为S元,有职工m名,
则S=q(p-40)×100-600m-13 200.又由图可得![]()
∴S=![]()
由已知,当p=52时,S=0,即(-2×52+140)(52-40)×100-600m-13 200=0,
解得m=50,即此时刻店有50名职工;
(2)由题意知
S=![]()
当40≤p≤58时,求得p=55时,S取得最大值7 800(元);
当58<p≤81时,求得p=61时,S的最大值6 900(元).
∴当p=55时,S有最大值7 800(元).
设该店最早可在n年后还清所有债务,依题意,12×7 800×n-268 000-200 000≥0,得n≥5.
即该店最早可在5年后还清所有债务,此时消费品价格定为每件55元.
17.(1)设第n层(自下而上,下同)摆放an只花盆,
则an=[20-(n-1)][14-(n-1)]=n2-36n+315(1≤n≤14),
(2)如果这样一堆花盆可以摆放7层,则第2层到笫7层的花盆总数为
S=S7-a1=(12+22+…+72)-36(1+2+…+7)+315×7-20×14=1 337-280=1 057,
故第一层每只花盆平均受力为![]() =7.55<8.
=7.55<8.
由于花盆的最下层承受压力最大,所以这堆花盆可以摆放7层,第7层花盆只数为112只.
如果这样一堆花盆可以摆放8层,则第2层到笫8层的花盆总数为S′=S+a 8=1 148只,
故第一层每只花盆平均受力为![]() =8.2>8.
=8.2>8.
所以,这堆花盆最多可摆放7层,花盆总数为1 337只.
18.(1)x∈[0,1)时,x-1∈[-1,0),
∴f1(x)=f(x-1)+1=sinπ(x-1)+1=1-sinπx.
x∈[1,2)时,x-1∈[0,1),∴f2(x)=f(x-1)+1=1-sinπ(x-1)+1=2+sinπx.
x∈[n,n+1),n≥-1,n∈Z时,
∴f n+1(x)=f(x-1)+1=f(x-2)+2=n+1+(-1) n+1sinπx.
(2)当x=n+![]() ,A n+1(n+
,A n+1(n+![]() ,n),B n+1(n+1,n+2),
,n),B n+1(n+1,n+2),![]() ,
,![]() =1,
=1,
![]() =4,
=4,![]() =4.
=4.
C n+1是平行四边形A n+1A n+2B n+2B n+1的对角线的交点,C n+1(n+![]() ,n+
,n+![]() ).
).
(3)第一类,例如:在(2)的条件下,点C n+1与C n+2之间具有怎样的数量关系.
解答:C n+1C n+2=2,
第二类,例如:在(2)的条件下,在C n+1与C n+2之间具有怎样的位置关系
解答:C n+1与C n+2在直线y=x+![]() 上.
上.
第三类,例如:把(2)的条件x=n+![]() 改成x∈[n,n+1)时,点C n+1an+1(x),bn+1(x))的运动曲线是什么?
改成x∈[n,n+1)时,点C n+1an+1(x),bn+1(x))的运动曲线是什么?
解答:
即yc=![]() 只需写出一个区间段上即可.
只需写出一个区间段上即可.
19. (1)在△ADE中,y2=x2+AE2-2x·AE·cos60°![]() y2=x2+AE2-x·AE,①
y2=x2+AE2-x·AE,①
又S△ADE=![]() S△ABC=
S△ABC=![]() a2=
a2=![]() x·AE·sin60°
x·AE·sin60°![]() x·AE=2a2.②
x·AE=2a2.②
②代入①得y2=x2+![]() -2a2(y>0),
-2a2(y>0),
∴y=![]() (a≤x≤2a).
(a≤x≤2a).
(2)如果DE是水管y=![]() ≥
≥![]() ,
,
当且仅当x2=![]() ,即x=
,即x=![]() a时“=”成立,故DE∥BC,且DE=
a时“=”成立,故DE∥BC,且DE=![]() a.
a.
如果DE是参观线路,记f(x)=x2+![]() ,可知函数在[a,
,可知函数在[a,![]() a]上递减,
a]上递减,
在[![]() a,2a]上递增,故f(x) max=f(a)=f(2a)=5a2.
a,2a]上递增,故f(x) max=f(a)=f(2a)=5a2.
∴y max=![]() .
.
即DE为AB中线或AC中线时,DE最长.
20. (1)设0≤x1<x2≤1,则必存在实数t∈(0,1),使得x2=x1+t,
由条件③得,f(x2)=f(x1+t)≥f(x1)+f(t)-2,
∴f(x2)-f(x1)≥f(t)-2,由条件②得,f(x2)-f(x1)≥0,故当0≤x≤1时,有f(0)≤f(x)≤f(1).
又在条件③中,令x1=0,x2=1,得f(1)≥f(1)+f(0)-2,即f(0)≤2,∴f(0)=2,故函数f(x)的最大值为3,最小值为2.
(2)在条件③中,令x1=x2=![]() ,得f(
,得f(![]() )≥2f(
)≥2f(![]() n)-2,即f(
n)-2,即f(![]() )-2≤
)-2≤![]() [f(
[f(![]() )-2],
)-2],
故当n∈N*时,有f(![]() )-2≤
)-2≤![]() [f(
[f(![]() )-2]≤
)-2]≤![]() [f(
[f(![]() )-2]≤…≤
)-2]≤…≤![]() [f(
[f(![]() )-2]=
)-2]= ![]() ,
,
即f(![]() )≤
)≤![]() +2.
+2.
又f(![]() )=f(1)=3≤2+
)=f(1)=3≤2+![]() ,
,
所以对一切n∈N,都有f(![]() )≤
)≤![]() +2.
+2.
(3)对一切x∈(0,1),都有f(x)<2x+2.
对任意满足x∈(0,1),总存在n(n∈N),使得![]() <x≤
<x≤![]() ,
,
根据(1)(2)结论,可知:f(x)≤f(![]() )≤
)≤![]() +2,且2x+2>2×
+2,且2x+2>2×![]() +2=
+2=![]() +2,
+2,
故有f(x)<2x+2.综上所述,对任意x∈(0,1),f(x)<2x+2恒成立.