解不等式基本训练题
一、选择题
(1)不等式6x2+5x<4的解集为( )
A![]() (-∞,-
(-∞,-![]() )∪(
)∪(![]() ,+∞) B
,+∞) B![]() (-
(- ![]() ,
,![]() )
)
C![]() (-
(- ![]() ,
,![]() )
D
)
D![]() (-∞,-
(-∞,-![]() )∪(
)∪(![]() ,+∞)
,+∞)
(2)a>0,b>0,不等式a>![]() >-b的解集为( )
>-b的解集为( )
A![]() -
-![]() <x<0或0<x<
<x<0或0<x<![]() B
B![]() -
- ![]() <x<
<x<![]()
C![]() x<-
x<-![]() 或x>
或x>![]() D
D![]() -
- ![]() <x<0或0<x<
<x<0或0<x<![]()
(3)不等式![]() (x-1)(x-2)2(x-3)<0的解集是( )
(x-1)(x-2)2(x-3)<0的解集是( )
A![]() (-1,1)∪(2,3)
B
(-1,1)∪(2,3)
B![]() (-∞,-1)∪(1,3)
(-∞,-1)∪(1,3)
C![]() (-∞,-1)∪(2,3)
D
(-∞,-1)∪(2,3)
D![]() R
R
(4)若a>0,且不等式ax2+bx+c<0无解,则左边的二次三项式的判别式()
A![]() Δ<0 B
Δ<0 B![]() Δ=0 C
Δ=0 C![]() Δ≤0 D
Δ≤0 D![]() Δ>0
Δ>0
(5)A={xx2+(p+2)x+1=0,x∈R},且R*∩A=![]() ,则有( )
,则有( )
A![]() p>-2 B
p>-2 B![]() p≥0
C
p≥0
C![]() -4<p<0 D
-4<p<0 D![]() p>-4
p>-4
(6)θ在第二象限,cosθ=![]() ,sinθ=
,sinθ=![]() ,则m满足( )
,则m满足( )
A![]() m<-5或m>3 B
m<-5或m>3 B![]() 3<m<9 C
3<m<9 C![]() m=0或m=8 D
m=0或m=8 D![]() m=8
m=8
(7)已知不等式loga(x2-x-2)>loga(-x2+2x+3)在x=![]() 时成立,则不等式的解集为
时成立,则不等式的解集为
A![]() {x1<x<2} B
{x1<x<2} B![]() {x2<x<
{x2<x<![]() } C
} C![]() {x1<x<
{x1<x<![]() } D
} D![]() {x2<x<5}
{x2<x<5}
(8)设0<b<![]() ,下列不等式恒成立的是( )
,下列不等式恒成立的是( )
A![]() b3>b
b3>b![]() B
B![]() logb(1-b)>1 C
logb(1-b)>1 C![]() cos(1+b)>cos(1-b) D
cos(1+b)>cos(1-b) D![]() (1-b)n<bn,n∈N
(1-b)n<bn,n∈N
(9)若不等式x2-logax<0在(0,![]() )内恒成立,则a满足( )
)内恒成立,则a满足( )
A![]()
![]() ≤a<1 B
≤a<1 B![]()
![]() <a<1
C
<a<1
C![]() 0<a≤
0<a≤![]() D
D![]() 0<a<
0<a<![]()
(10)不等式![]() 的解集是( )
的解集是( )
A![]() [0,1] B
[0,1] B![]() [0,+∞] C
[0,+∞] C![]() (1,+∞) D
(1,+∞) D![]() [-1,1]
[-1,1]
(11)不等式![]() 的解集是( )
的解集是( )
A![]()
![]() B
B![]() (1,2)
C
(1,2)
C![]() (2,+∞) D
(2,+∞) D![]() (1,+∞)
(1,+∞)
(12)不等式(x-1)![]() ≥0的解集是( )
≥0的解集是( )
A![]() {xx>1}
B
{xx>1}
B![]() {xx≥1或x=-2} C
{xx≥1或x=-2} C![]() {xx≥1} D
{xx≥1} D![]() {xx≥-2且x≠1}
{xx≥-2且x≠1}
(13)函数f(x)=![]() 的定义域为A,函数g(x)=
的定义域为A,函数g(x)=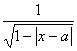 的定义域为B,则使A∩B=
的定义域为B,则使A∩B=![]() ,实数a的取值范围是( )
,实数a的取值范围是( )
A![]() {a-1<a<3} B
{a-1<a<3} B![]() {a-2<a<4} C
{a-2<a<4} C![]() {a-2≤a≤4} D
{a-2≤a≤4} D![]() {a-1≤a≤3}
{a-1≤a≤3}
(14)关于x的不等式![]() <2x+a(a>0)的解集为( )
<2x+a(a>0)的解集为( )
A![]() (0,a) B
(0,a) B![]() (0,a] C
(0,a] C![]() (0,+∞)∪(-∞,-
(0,+∞)∪(-∞,-![]() a)
D
a)
D![]()
![]()
二.填空题
(15)不等式1≤x-2≤7的解集是
![]()
(16)不等式![]() >a的解集是
>a的解集是 ![]()
(17)不等式lgx-4<-1的解集是
![]()
(18)不等式![]() <a(a>0,b>0,c>0)的解集是
<a(a>0,b>0,c>0)的解集是 ![]()
(19)若不等式![]() <0的解为-1<x<5,则a=
<0的解为-1<x<5,则a= ![]()
(20)不等式![]() <3-lgx的解集是
<3-lgx的解集是 ![]()
(21)函数f(x)=log2(x2-4),g(x)=2![]() (k<-1),则f(x)g(x)的定义域为
(k<-1),则f(x)g(x)的定义域为 ![]() 三、解答题
三、解答题
(22)解下列不等式
(1)(x+4)(x+5)2>(3x-2)(x+5)2;
(2)![]() ≤0;
≤0;
(3)![]() ≥3
≥3
(23)设不等式(2x-1)>m(x2-1)对满足m≤2的一切实数m的值都成立,求x的取值范围![]()
解不等式练习题参考答案:
1.B 2.C 3.B 4.C 5.B 6.D 7.B
8.C 9.A 10.A 11.D 12.B 13.D 14.B
15.[-5,1]∪[3,9]
16.a=0时x>0;a>0时,0<x<![]() ;a<0时,x<
;a<0时,x<![]() 或x>0
或x>0
17.{x4<x<![]() 或
或![]() <x<4}
<x<4}
18.{xx<b或x>b-![]() } 19.4 20.10≤x<100 21.[2k-2)∪(2,+∞)
} 19.4 20.10≤x<100 21.[2k-2)∪(2,+∞)
22.解:(1)当x≠-5时,(x+5)2>0,两边同除以(x+5)2得x+4>3x-2,
即x<3且x≠-5;∴x∈(-∞,-5)∪(-5,3)
(2)当x≠4时,原不等式![]() (x-1)(x-3)(x+1)≤0(x≠-1)
(x-1)(x-3)(x+1)≤0(x≠-1) ![]() 1≤x≤3或x<-1,当x=4时,显然左边=0,不等式成立
1≤x≤3或x<-1,当x=4时,显然左边=0,不等式成立![]()
故原不等式的解集为{x1≤x≤3或x<-1或x=4}![]()
(3)原不等式可化为![]() -3≥0
-3≥0![]()
![]() ∴x∈(-∞,1)∪[2,3]∪(4,+∞)
∴x∈(-∞,1)∪[2,3]∪(4,+∞)![]()
23.解:①若x2-1=0,即x=±1,且2x-1>0,即x>![]() 时,此时x=1,原不等式对m≤2恒成立;
时,此时x=1,原不等式对m≤2恒成立;
②若x2-1>0,要使![]() >m,对m≤2恒成立,只要
>m,对m≤2恒成立,只要![]() >2,即
>2,即
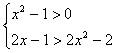 得1<x<
得1<x<![]()
![]()
③若x2-1<0时,要使![]() <m,对m≤2恒成立,只要
<m,对m≤2恒成立,只要![]() <-2,即
<-2,即
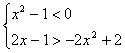 得
得![]() <x<1
<x<1![]()
综合①②③得,所求x的范围为![]() <x<
<x<![]()
![]()