高考数学三基小题训练一
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
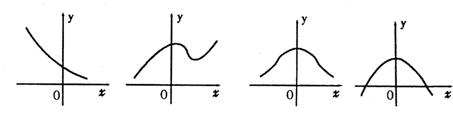
1.函数y=2x+1的图象是 ( )
 2.△ABC中,cosA=
2.△ABC中,cosA=![]() ,sinB=
,sinB=![]() ,则cosC的值为 ( )
,则cosC的值为 ( )
A.![]() B.-
B.-![]() C.-
C.-![]() D.
D. ![]()
3.过点(1,3)作直线l,若l经过点(a,0)和(0,b),且a,b∈N*,则可作出的l的条数为( )
A.1 B.2 C.3 D.多于3
4.函数f(x)=logax(a>0且a≠1)对任意正实数x,y都有 ( )
A.f(x·y)=f(x)·f(y) B.f(x·y)=f(x)+f(y)
C.f(x+y)=f(x)·f(y) D.f(x+y)=f(x)+f(y)
5.已知二面角α—l—β的大小为60°,b和c是两条异面直线,则在下列四个条件中,能使b和c所成的角为60°的是( )
A.b∥α,c∥β B.b∥α,c⊥β
C.b⊥α,c⊥β D.b⊥α,c∥β
6.一个等差数列共n项,其和为90,这个数列的前10项的和为25,后10项的和为75,则项数n为 ( )
A.14 B.16 C.18 D.20
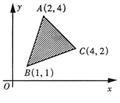
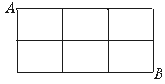 7.某城市的街道如图,某人要从A地前往B地,则路程最短的走法有 ( )
7.某城市的街道如图,某人要从A地前往B地,则路程最短的走法有 ( )
A.8种 B.10种
C.12种 D.32种
8.若a,b是异面直线,a![]() α,b
α,b![]() β,α∩β=l,则下列命题中是真命题的为( )
β,α∩β=l,则下列命题中是真命题的为( )
A.l与a、b分别相交 B.l与a、b都不相交
C.l至多与a、b中的一条相交 D.l至少与a、b中的一条相交
9.设F1,F2是双曲线![]() -y2=1的两个焦点,点P在双曲线上,且
-y2=1的两个焦点,点P在双曲线上,且![]() ·
·![]() =0,则
=0,则![]() ·
·![]() 的值等于( )
的值等于( )
A.2 B.2![]() C.4 D.8
C.4 D.8
10.f(x)=(1+2x)m+(1+3x)n(m,n∈N*)的展开式中x的系数为13,则x2的系数为( )
A.31 B.40 C.31或40 D.71或80
11.从装有4粒大小、形状相同,颜色不同的玻璃球的瓶中,随意一次倒出若干粒玻璃球(至少一粒),则倒出奇数粒玻璃球的概率比倒出偶数粒玻璃球的概率( )
A.小 B.大 C.相等 D.大小不能确定
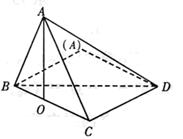
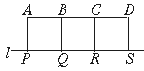 12.如右图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在(
)
12.如右图,A、B、C、D是某煤矿的四个采煤点,l是公路,图中所标线段为道路,ABQP、BCRQ、CDSR近似于正方形.已知A、B、C、D四个采煤点每天的采煤量之比约为5∶1∶2∶3,运煤的费用与运煤的路程、所运煤的重量都成正比.现要从P、Q、R、S中选出一处设立一个运煤中转站,使四个采煤点的煤运到中转站的费用最少,则地点应选在(
)
A.P点 B.Q点 C.R点 D.S点
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13.抛物线y2=2x上到直线x-y+3=0距离最短的点的坐标为_________.
14.一个长方体共一顶点的三个面的面积分别是![]() ,
,![]() ,
,![]() ,这个长方体对角线的长是_________.
,这个长方体对角线的长是_________.
15.设定义在R上的偶函数f(x)满足f(x+1)+f(x)=1,且当x∈[1,2]时,f(x)=2-x,则f(8.5)=_________.
16.某校要从甲、乙两名优秀短跑选手中选一名选手参加全市中学生田径百米比赛,该校预先对这两名选手测试了8次,测试成绩如下:
| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 | 第7次 | 第8次 | |
| 甲成绩(秒) | 12.1 | 12.2 | 13 | 12.5 | 13.1 | 12.5 | 12.4 | 12.2 |
| 乙成绩(秒) | 12 | 12.4 | 12.8 | 13 | 12.2 | 12.8 | 12.3 | 12.5 |
根据测试成绩,派_________(填甲或乙)选手参赛更好,理由是____________________.
答案:
一、1.A 2.D 3.B 4.B 5.C 6.C 7.B 8.D 9.A 10.C 11.B 12.B
二、13.(![]() ,1) 14.
,1) 14.![]() 15.
15. ![]()
三基小题训练二
命题:王统好
 一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.如图,点O是正六边形ABCDEF的中心,则以图中点
A、B、C、D、E、F、O中的任意一点为始点,与始点不
同的另一点为终点的所有向量中,除向量![]() 外,与向量
外,与向量
![]() 共线的向量共有(
)
共线的向量共有(
)
A.2个 B. 3个 C.6个 D. 7个
2.已知曲线C:y2=2px上一点P的横坐标为4,P到焦点的距离为5,则曲线C的焦点到准线的距离为 ( )
A. ![]() B. 1
C. 2
D. 4
B. 1
C. 2
D. 4
3.若(3a2
-![]() ) n 展开式中含有常数项,则正整数n的最小值是 ( )
) n 展开式中含有常数项,则正整数n的最小值是 ( )
A.4 B.5 C. 6 D. 8
4. 从5名演员中选3人参加表演,其中甲在乙前表演的概率为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5.抛物线y2=a(x+1)的准线方程是x=-3,则这条抛物线的焦点坐标是( )
A.(3,0) B.(2,0) C.(1,0) D.(-1,0)
6.已知向量m=(a,b),向量n⊥m,且|n|=|m|,则n的坐标可以为( )
A.(a,-b) B.(-a,b) C.(b,-a) D.(-b,-a)
7. 如果S={x|x=2n+1,n∈Z},T={x|x=4n±1,n∈Z},那么
A.S![]() T
B.T
T
B.T![]() S
C.S=T
D.S≠T
S
C.S=T
D.S≠T
8.有6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有 ( )
A.36种 B.48种 C.72种 D.96种
9.已知直线l、m,平面α、β,且l⊥α,m![]() β.给出四个命题:(1)若α∥β,则l⊥m;
β.给出四个命题:(1)若α∥β,则l⊥m;
(2)若l⊥m,则α∥β;(3)若α⊥β,则l∥m;(4)若l∥m,则α⊥β,其中正确的命题个数是( )
A.4 B.1 C.3 D.2
10.已知函数f(x)=log2(x2-ax+3a)在区间[2,+∞)上递增,则实数a的取值范围是( )
A.(-∞,4) B.(-4,4] C.(-∞,-4)∪[2,+∞) D.[-4,2)
11.4只笔与5本书的价格之和小于22元,而6只笔与3本书的价格之和大于24元,则2只笔与3本书的价格比较( )
A.2只笔贵 B.3本书贵 C.二者相同 D.无法确定
12.若α是锐角,sin(α-![]() )=
)=![]() ,则cosα的值等于
,则cosα的值等于
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
二、填空题:本大题共4小题,每小题4分,共16分.答案填在题中横线上.
13.在等差数列{an}中,a1=![]() ,第10项开始比1大,则公差d的取值范围是___________.
,第10项开始比1大,则公差d的取值范围是___________.
14.已知正三棱柱ABC—A1B1C1,底面边长与侧棱长的比为![]() ∶1,则直线AB1与CA1所成的角为
。
∶1,则直线AB1与CA1所成的角为
。
15.若sin2α<0,sinαcosα<0,
化简cosα![]() +sinα
+sinα![]() = ______________.
= ______________.
16.已知函数f(x)满足:f(p+q)=f(p)f(q),f(1)=3,则
![]() =
.
=
.
答案:
一.
1 D; 2 A ; 3 B; 4 A ; 5 C; 6 C; 7 C; 8 C ; 9 D ; 10 B; 11 A ; 12 A .
二.
13. ![]() <d《
<d《![]() ; 14. 90°; 15
; 14. 90°; 15 ![]() sin(α-
sin(α-![]() ); 16 24.
); 16 24.
三基小题训练三
命题:王统好
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设集合P={3,4,5},Q={4,5,6,7},定义P★Q={(![]() 则P★Q中
则P★Q中
元素的个数为 ( )
A.3 B.7 C.10 D.12
|
A B C D
3.在![]() 的展开式中,含
的展开式中,含![]() 项的系数是首项为-2,公差为3的等
项的系数是首项为-2,公差为3的等
差数列的 ( )
A.第13项 B.第18项 C.第11项 D.第20项
4.有一块直角三角板ABC,∠A=30°,∠B=90°,BC边在桌面上,当三角板所在平面与
桌面成45°角时,AB边与桌面所成的角等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若将函数![]() 的图象按向量
的图象按向量![]() 平移,使图象上点P的坐标由(1,0)变为(2,2),
平移,使图象上点P的坐标由(1,0)变为(2,2),
则平移后图象的解析式为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.直线![]() 的倾斜角为 ( )
的倾斜角为 ( )
A.40° B.50° C.130° D.140°
7.一个容量为20的样本,数据的分组及各组的频数如下:(10,20![]() ,2;(20,30
,2;(20,30![]() ,3;
,3;
(30,40![]() ,4;(40,50
,4;(40,50![]() ,5;(50,60
,5;(50,60![]() ,4;(60,70
,4;(60,70![]() ,2. 则样本在区间(10,50
,2. 则样本在区间(10,50![]() 上
上
的频率为 ( )
A.0.5 B.0.7 C.0.25 D.0.05
8.在抛物线![]() 上有点M,它到直线
上有点M,它到直线![]() 的距离为4
的距离为4![]() ,如果点M的坐标为(
,如果点M的坐标为(![]() ),
),
且![]() 的值为 ( )
的值为 ( )
A.![]() B.1 C.
B.1 C.![]() D.2
D.2
9.已知双曲线![]() ,在两条渐近线所构成的角中,
,在两条渐近线所构成的角中,
设以实轴为角平分线的角为![]() ,则
,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.按ABO血型系统学说,每个人的血型为A,B,O,AB型四种之一,依血型遗传学,
当且仅当父母中至少有一人的血型是AB型时,子女的血型一定不是O型,若某人的血
型的O型,则父母血型的所有可能情况有 ( )
A.12种 B.6种 C.10种 D.9种
11.正四面体的四个顶点都在一个球面上,且正四面体的高为4,则球的表面积为 ( )
A.16(12-6![]() B.18
B.18![]()
C.36![]() D.64(6-4
D.64(6-4![]()
12.一机器狗每秒钟前进或后退一步,程序设计师让机器狗以前进3步,然后再后退2步的
规律移动.如果将此机器狗放在数轴的原点,面向正方向,以1步的距离为1单位长移动,令P(![]() )表示第
)表示第![]() 秒时机器狗所在位置的坐标,且P(0)=0,则下列结论中错误的是( )
秒时机器狗所在位置的坐标,且P(0)=0,则下列结论中错误的是( )
A.P(3)=3 B.P(5)=5 C.P(101)=21 D.P(101)<P(104)
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
13.在等比数列{![]() ,且公比
,且公比![]() 是整数,则
是整数,则![]() 等于
.
等于
.
14.若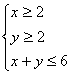 ,则目标函数
,则目标函数![]() 的取值范围是
.
的取值范围是
.
15.已知![]() 那么
那么![]() .
.
16.取棱长为![]() 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,依次进行下去,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体.则此多面体:①有12个顶点;②有24条棱;③有12个面;④表面积为
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,依次进行下去,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体.则此多面体:①有12个顶点;②有24条棱;③有12个面;④表面积为![]() ;⑤体积为
;⑤体积为![]() . 以上结论正确的是 .(要求填上的有正确结论的序号)
. 以上结论正确的是 .(要求填上的有正确结论的序号)
答案:一、选择题:
1.D 2.C 3.D 4.A 5.C 6.B 7.B 8.D 9.C 10.D 11.C 12.C
二、填空题:
13.-1或512;14.[8,14];15.4;16.①②⑤
三基小题训练四
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.满足x-1+y-1≤1的图形面积为
A.1 B.![]() C.2
D.4
C.2
D.4
2.不等式x+log3x<x+log3x的解集为
A.(0,1) B.(1,+∞) C.(0,+∞) D.(-∞,+∞)
3.已知双曲线的焦点到渐近线的距离等于右焦点到右顶点的距离的2倍,则双曲线的离心率e的值为
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
4.一个等差数列{an}中,a1=-5,它的前11项的平均值是5,若从中抽取一项,余下项的平均值是4,则抽取的是
A.a11 B.a10 C.a9 D.a8
5.设函数f(x)=logax(a>0,且a≠1)满足f(9)=2,则f-1(log92)等于
A.2
B.![]() C.
C.![]() D.±
D.±![]()
6.将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥D—ABC的体积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设O、A、B、C为平面上四个点,![]() =a,
=a,![]() =b,
=b,![]() =c,且a+b+c=0,
=c,且a+b+c=0,
a·b=b·c=c·a=-1,则a+b+c等于
A.2![]() B.2
B.2![]() C.3
C.3![]() D.3
D.3![]()
8.将函数y=f(x)sinx的图象向右平移![]() 个单位,再作关于x轴的对称曲线,得到函数y=1-2sin2x的图象,则f(x)是
个单位,再作关于x轴的对称曲线,得到函数y=1-2sin2x的图象,则f(x)是
A.cosx B.2cosx C.sinx D.2sinx
9.椭圆![]() =1上一点P到两焦点的距离之积为m,当m取最大值时,P点坐标为 A.(5,0),(-5,0)
B.(
=1上一点P到两焦点的距离之积为m,当m取最大值时,P点坐标为 A.(5,0),(-5,0)
B.(![]() )(
)(![]() )
)
C.(![]() )(-
)(-![]() ) D.(0,-3)(0,3)
) D.(0,-3)(0,3)
10.已知P箱中有红球1个,白球9个,Q箱中有白球7个,(P、Q箱中所有的球除颜色外完全相同).现随意从P箱中取出3个球放入Q箱,将Q箱中的球充分搅匀后,再从Q箱中随意取出3个球放入P箱,则红球从P箱移到Q箱,再从Q箱返回P箱中的概率等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.一个容量为20的样本数据,分组后,组距与频数如下:
(10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70),2,则样本在(-∞,50)上的频率为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
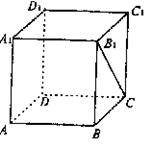
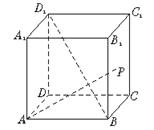 12.如图,正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则动点P的轨迹是
12.如图,正方体ABCD—A1B1C1D1中,点P在侧面BCC1B1及其边界上运动,并且总是保持AP⊥BD1,则动点P的轨迹是
A .线段B1C B. 线段BC1
C .BB1中点与CC1中点连成的线段
D. BC中点与B1C1中点连成的线段
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13.已知(![]() )6的展开式中,不含x的项是
)6的展开式中,不含x的项是![]() ,则p的值是______.
,则p的值是______.
14.点P在曲线y=x3-x+![]() 上移动,设过点P的切线的倾斜角为α,则α的取值范围是______.
上移动,设过点P的切线的倾斜角为α,则α的取值范围是______.
![]() 15.在如图的1×6矩形长条中涂上红、黄、蓝三种颜色,每种颜色限涂两格,且相邻两格不同色,则不同的涂色方案有______种.
15.在如图的1×6矩形长条中涂上红、黄、蓝三种颜色,每种颜色限涂两格,且相邻两格不同色,则不同的涂色方案有______种.
16.同一个与正方体各面都不平行的平面去截正方体,截得的截面是四边形的图形可能是①矩形;②直角梯形;③菱形;④正方形中的______(写出所有可能图形的序号).
答案:
一、1.C 2.A 3.B 4.A 5.B 6.D 7.C 8.B 9.D 10.B 11.D 12.A
二、13.3 14.[0,![]()
![]() ∪[
∪[![]() ,π
,π![]() 15.30 16.①③④
15.30 16.①③④
三基小题训练五
命题:王统好
一、选择题本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的.
1.在数列![]() 则此数列的前4项之和为 ( )
则此数列的前4项之和为 ( )
A.0 B.1 C.2 D.-2
2.函数![]() 的值域是 ( )
的值域是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.对总数为N的一批零件抽取一个容量为30的样本,若每个零件被抽取的概率为![]() ,则N的值( )
,则N的值( )
A.120 B.200 C.150 D.100
4.若函数![]() 的表达式是( )
的表达式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.设![]() 的展开式中,二项式系数的和为256,则此二项展开式中系数最小的项是( )
的展开式中,二项式系数的和为256,则此二项展开式中系数最小的项是( )
A.第5项 B.第4、5两项 C.第5、6两项 D.第4、6两项
6.已知i , j为互相垂直的单位向量,![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知![]() ,
,
![]() 满足的关系是 ( )
满足的关系是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 从湖中打一网鱼,共M条,做上记号再放回湖中,数天后再打一网鱼共有n条,其中有k条有记号,则能估计湖中有鱼 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.函数![]() 有且只有一个实根,那么实数a应满足( )
有且只有一个实根,那么实数a应满足( )
A.a<0 B.0<a<1 C.a=0 D.a>1
10.设![]() 为坐标平面内一点,O为坐标原点,记f(x)=OM,当x变化时,函数 f(x)的最小正周期是 ( )
为坐标平面内一点,O为坐标原点,记f(x)=OM,当x变化时,函数 f(x)的最小正周期是 ( )
A.30π B.15π C.30 D.15
11.若函数![]() 在R上单调递增,则实数a, b一定满足的条件是( )
在R上单调递增,则实数a, b一定满足的条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知函数图象![]() 关于点(2,-3)对称,则a的值为 ( )
关于点(2,-3)对称,则a的值为 ( )
A.3 B.-2 C.2 D.-3
二、填空题:本大题有4小题,每小题4分,共16分.请将答案填写在题中的横线上.
13.“面积相等的三角形全等”的否命题是 命题(填“真”或者“假”)
14.已知![]() 的值为
的值为
15.某乡镇现有人口1万,经长期贯彻国家计划生育政策,目前每年出生人数与死亡人数分别为年初人口的0.8%和1.2%,则经过2年后,该镇人口数应为 万.(结果精确到0.01)
16.“渐升数”是指每个数字比其左边的数字大的正整数(如34689).则五位“渐升数”共有 个,若把这些数按从小到大的顺序排列,则第100个数为 .
一、选择题:本大题共12小题,每小题5分,共60分.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 13 |
| 答案 | A | D | A | B | D | B | C | A | C | D | A | C |
二、填空题:本大题共4小题,每小题4分,共16分.
13.真 14.![]() 15.0.99 16.126, 24789
15.0.99 16.126, 24789
三基小题训练六
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 给出两个命题:p:x=x的充要条件是x为正实数;q:存在反函数的函数一定是单调函
数,则下列哪个复合命题是真命题 ( )
A.p且q B.p或q C.┐p且q D.┐p或q
2.给出下列命题:
![]()
其中正确的判断是( )
A.①④ B.①② C.②③ D.①②④
3.抛物线y=ax2(a<0)的焦点坐标是( )
A.(0,![]() ) B.(0,
) B.(0,![]() )
C.(0,-
)
C.(0,-![]() ) D.(-
) D.(-![]() ,0)
,0)
![]() 4.计算机是将信息转换成二进制进行处理的,二进制即“逢2进1”如(1101)2表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数
4.计算机是将信息转换成二进制进行处理的,二进制即“逢2进1”如(1101)2表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数
转换成十进制形式是( )
A.217-2 B.216-2 C.216-1 D.215-1
5.已知f(cosx)=cos3x,则f(sin30°)的值是( )
A.1 B.![]() C.0 D.-1
C.0 D.-1
6.已知y=f(x)是偶函数,当x>0时,f(x)=x+![]() ,当x∈[-3,-1]时,记f(x)的最大值为m,最小值为n,则m-n等于( )
,当x∈[-3,-1]时,记f(x)的最大值为m,最小值为n,则m-n等于( )
A.2 B.1
C.3 D.![]()
7.某村有旱地与水田若干,现在需要估计平均亩产量,用按5%比例分层抽样的方法抽取了15亩旱地45亩水田进行调查,则这个村的旱地与水田的亩数分别为( )
A.150,450 B.300,900 C.600,600 D.75,225
8.已知两点A(-1,0),B(0,2),点P是椭圆![]() =1上的动点,则△PAB面积的最大值为( )
=1上的动点,则△PAB面积的最大值为( )
A.4+![]() B.4+
B.4+![]() C.2+
C.2+![]() D.2+
D.2+![]()
9.设向量a=(x1,y1),b=(x2,y2),则下列为a与b共线的充要条件的有( )
①存在一个实数λ,使得a=λb或b=λa
;②a·b=a·b;③![]() ;④(a+b)∥(a-b).
;④(a+b)∥(a-b).
A.1个 B.2个 C.3个 D.4个
 10.点P是球O的直径AB上的动点,PA=x,过点P 且与AB垂直的截面面积记为y,则y=
10.点P是球O的直径AB上的动点,PA=x,过点P 且与AB垂直的截面面积记为y,则y=![]() f(x)的大致图象是
f(x)的大致图象是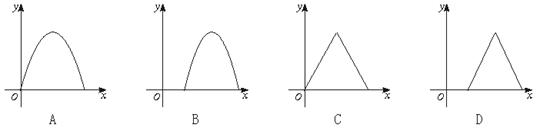 11.三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲手中, 则不同的传球方式共有
11.三人互相传球,由甲开始发球,并作为第一次传球,经过5次传球后,球仍回到甲手中, 则不同的传球方式共有
A.6种 B.10种 C.8种 D.16种
12.已知点F1、F2分别是双曲线![]() =1的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2为锐角三角形,则该双曲线的离心率e的取值范围是
=1的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2为锐角三角形,则该双曲线的离心率e的取值范围是
A.(1,+∞) B.(1,![]() ) C.(
) C.(![]() -1,1+
-1,1+![]() ) D.(1,1+
) D.(1,1+![]() )
)
二、填空题(本大题共4小题,每小题4分,共16分.把答案填在题中横线上)
13.方程log2x=x2-2的实根的个数为______.
14.1996年的诺贝尔化学奖授予对发现C60有重大贡献的三位科学家.C60是由60个C原子组成的分子,它结构为简单多面体形状.这个多面体有60个顶点,从每个顶点都引出3条棱,各面的形状分为五边形或六边形两种,则C60分子中形状为五边形的面有______个,形状为六边形的面有______个.
15.在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为______.
16.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上是增函数,给出下列关于f(x)的判断:
①f(x)是周期函数;②f(x)关于直线x=1对称;③f(x)在[0,1]上是增函数;④f(x)在
[1,2]上是减函数;⑤f(2)=f(0),其中正确判断的序号为______(写出所有正确判断的序号).
答案:
一、1.D 2.B 3.B 4.C 5.D 6.B 7.A8.B 9.C 10.A 11.C 12.D
二、13.4 14.12 20 15.13 16.①②⑤
三基小题训练七
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.准线方程为![]() 的抛物线的标准方程为 ( )
的抛物线的标准方程为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.函数![]() 是 ( )
是 ( )
A.最小正周期为π的奇函数 B.最小正周期为π的偶函数
C.最小正周期为2π的奇函数 D.最小正周期为2π的偶函数
3.函数![]() 的反函数是 ( )
的反函数是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知向量![]() 平行,则x等于 ( )
平行,则x等于 ( )
A.-6 B.6 C.-4 D.4
5.![]() 是直线
是直线![]() 垂直的 ( )
垂直的 ( )
A.充分而不必要的条件 B.必要而不充分的条件
C.充要条件 D.既不充分又不必要的条件
6.已知直线a、b与平面α,给出下列四个命题
①若a∥b,b![]() α,则a∥α; ②若a∥α,b
α,则a∥α; ②若a∥α,b![]() α,则a∥b ;
α,则a∥b ;
③若a∥α,b∥α,则a∥b; ④a⊥α,b∥α,则a⊥b.
其中正确的命题是 ( )
A.1个 B.2个 C.3个 D.4个
7.函数![]() 的单调递增区间是 ( )
的单调递增区间是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.设集合M=![]() 是 ( )
是 ( )
A.![]() B.有限集 C.M D.N
B.有限集 C.M D.N
9.已知函数![]() 的最小值是 ( )
的最小值是 ( )
A.![]() B.2 C.
B.2 C.![]() D.
D. ![]()
10.若双曲线![]() 的左支上一点P(a,b)到直线
的左支上一点P(a,b)到直线![]() 的距离为
的距离为![]() +b的值为( )
+b的值为( )
A.![]() B.
B.![]() C.-2 D.2
C.-2 D.2
11.若一个四面体由长度为1,2,3的三种棱所构成,则这样的四面体的个数是 ( )
A.2 B.4 C.6 D.8
12.某债券市场常年发行三种债券,A种面值为1000元,一年到期本息和为1040元;B种贴水债券面值为1000元,但买入价为960元,一年到期本息和为1000元;C种面值为1000元,半年到期本息和为1020元. 设这三种债券的年收益率分别为a, b, c,则a, b, c的大小关系是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题:(本大题共4小题,每小题4分,共16分,把答案直接填在题中横线上.)
13.某校有初中学生1200人,高中学生900人,老师120人,现用分层抽样方法从所有师生中抽取一个容量为N的样本进行调查,如果应从高中学生中抽取60人,那么N
.
14.在经济学中,定义![]() 的边际函数,某企业的一种产品的利润函数
的边际函数,某企业的一种产品的利润函数![]() *),则它的边际函数MP(x)=
.(注:用多项式表示)
*),则它的边际函数MP(x)=
.(注:用多项式表示)
15.已知![]() 分别为△ABC的三边,且
分别为△ABC的三边,且![]() .
.
16.已知下列四个函数:①![]() ②
②![]() ③
③![]() ④
④![]() .其中图象不经过第一象限的函数有
.(注:把你认为符合条件的函数的序号都填上)
.其中图象不经过第一象限的函数有
.(注:把你认为符合条件的函数的序号都填上)
答案:
一、选择题:(每小题5分,共60分)
BADCA ABDCA BC
二、填空题:(每小题4分,共16分)
13.148; 14.![]() 且
且![]() (未标定义域扣1分);
(未标定义域扣1分);
15.![]() ; 16.①,④(多填少填均不给分)
; 16.①,④(多填少填均不给分)
三基小题训练八
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题所给出的四个选项中,只
有一项是符合题目要求的)
1.直线![]() 的倾斜角的取值范围是 ( )
的倾斜角的取值范围是 ( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设方程![]() 的根为α,[α]表示不超过α的最大整数,则[α]是 ( )
的根为α,[α]表示不超过α的最大整数,则[α]是 ( )
A.1 B.2 C.3 D.4
3.若“p且q”与“p或q”均为假命题,则 ( )
A.命题“非p”与“非q”的真值不同 B.命题“非p”与“非q”至少有一个是假命题
C.命题“非p”与“q”的真值相同 D.命题“非p”与“非q”都是真命题
4.设1!,2!,3!,……,n!的和为Sn,则Sn的个位数是 ( )
A.1 B.3 C.5 D.7
5.有下列命题①![]() =
=![]() ;②(
;②(![]() )=
)=![]() ;③若
;③若![]() =(
=(![]() ,4),则
,4),则![]() =
=![]() 的充要条件是
的充要条件是![]() =
=![]() ;④若
;④若![]() 的起点为
的起点为![]() ,终点为
,终点为![]() ,则
,则![]() 与
与![]() 轴正向所夹角的余弦值是
轴正向所夹角的余弦值是![]() ,其中正确命题的序号是 ( )
,其中正确命题的序号是 ( )
A.①② B.②③ C.②④ D.③④
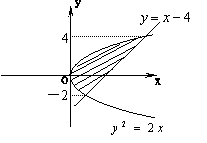 6.右图中,阴影部分的面积是 ( )
6.右图中,阴影部分的面积是 ( )
A.16 B.18 C.20 D.22
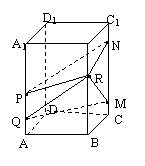
7.如图,正四棱柱ABCD–A1B1C1D1中,AB=3,BB1=4.长为1的线段PQ在棱AA1上移动,长为3的线段MN在棱CC1上移动,点R在棱BB1上移动,则四棱锥R–PQMN的体积是( )
A.6 B.10 C.12 D.不确定
8.用1,2,3,4这四个数字可排成必须含有重复数字的四位数有 ( )
A.265个 B.232个 C.128个 D.24个
9.已知定点![]() ,
,![]() ,动点
,动点![]() 在
在![]() 轴正半轴上,若
轴正半轴上,若![]() 取得最大值,则
取得最大值,则![]() 点的坐标( )
点的坐标( )
A.![]() B.
B.![]() C.
C.![]() D.这样的点
D.这样的点![]() 不存在
不存在
 10.设
10.设![]() 、
、![]() 、
、![]() 、
、![]() 均为正数,且
均为正数,且![]() 、
、![]() 为常数,
为常数,![]() 、
、![]() 为变量.若
为变量.若![]() ,则
,则![]() 的最大值为 ( ) A.
的最大值为 ( ) A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
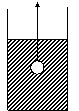
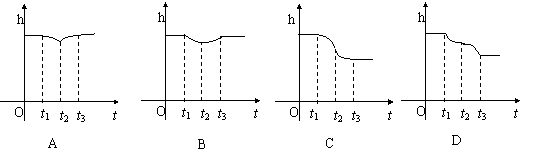
11.如图所示,在一个盛 水的圆柱形容器内的水面以下,有一个用细线吊着的
下端开了一个很小的孔的充满水的薄壁小球,当慢慢地匀速地将小球从水下向水
面以上拉动时,圆柱形容器内水面的高度h与时间t的函数图像大致是( )
 |
12.4个茶杯荷5包茶叶的价格之和小于22元,而6个茶杯和3包茶叶的价格之和大于24,则2个茶杯和3包茶叶的价格比较 ( )
A.2个茶杯贵 B.2包茶叶贵 C.二者相同 D.无法确定
 二、填空题(本大题共4小题,每小题4分,共16分。把答案填在题中横线上)
二、填空题(本大题共4小题,每小题4分,共16分。把答案填在题中横线上)
 13.对于在区间[
13.对于在区间[![]() ,
,![]() ]上有意义的两个函数
]上有意义的两个函数![]() 和
和![]() ,如果对任意
,如果对任意![]() ,均有
,均有![]() ,那么我们称
,那么我们称![]() 和
和![]() 在[
在[![]() ,
,![]() ]上是接近的.若函数
]上是接近的.若函数![]() 与
与![]() 在[
在[![]() ,
,![]() ] 上是接近的,则该区间可以是 .
] 上是接近的,则该区间可以是 .
14.在等差数列![]() 中,已知前20项之和
中,已知前20项之和![]() ,则
,则![]() .
.
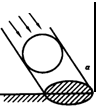
15.如图,一广告气球被一束入射角为![]() 的平行光线照射,其投影是长半轴长为
的平行光线照射,其投影是长半轴长为
5米的椭圆,则制作这个广告气球至少需要的面料为 .
16.由![]() 及
及![]() 围成几何图形的面积是
.
围成几何图形的面积是
.
答案:一、选择题
D B D B C ,B A B C C ,C A
二、填空题:
13. [1,2]∪[3,4]
14. 34 15. ![]() 16. 3
16. 3
三基小题训练九
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.集合A={xx=2k,k∈Z},B={xx=2k+1,k∈Z},C={xx=4k+1,k∈Z},又a∈A,b∈B,则有
A.a+b∈A
B.a+b∈B
C.a+b∈C
D.a+b不属于A,B,C中的任意一个
2.已知f(x)=sin(x+![]() ,g(x)=cos(x-
,g(x)=cos(x-![]() ),则f(x)的图象
),则f(x)的图象
A.与g(x)的图象相同
B.与g(x)的图象关于y轴对称
C.向左平移![]() 个单位,得到g(x)的图象
个单位,得到g(x)的图象
D.向右平移![]() 个单位,得到g(x)的图象
个单位,得到g(x)的图象
3.过原点的直线与圆x2+y2+4x+3=0相切,若切点在第三象限,则该直线的方程是
A.y=![]() x B.y=-
x B.y=-![]() x
x
C.y=![]() x D.y=-
x D.y=-![]() x
x
4.函数y=1-![]() , 则下列说法正确的是
, 则下列说法正确的是
A.y在(-1,+∞)内单调递增 B.y在(-1,+∞)内单调递减
C.y在(1,+∞)内单调递增 D.y在(1,+∞)内单调递减
5.已知直线m,n和平面![]() ,那么m∥n的一个必要但非充分条件是
,那么m∥n的一个必要但非充分条件是
A.m∥![]() ,n∥
,n∥![]() B.m⊥
B.m⊥![]() ,n⊥
,n⊥![]()
C.m∥![]() 且n
且n![]()
![]() D.m,n与
D.m,n与![]() 成等角
成等角
6.在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本:①采用随机抽样法,将零件编号为00,01,02,…,99,抽出20个;②采用系统抽样法,将所有零件分成20组,每组5个,然后每组中随机抽取1个;③采用分层抽样法,随机从一级品中抽取4个,二级品中抽取6个,三级品中抽取10个;则
A.不论采取哪种抽样方法,这100个零件中每个被抽到的概率都是![]()
B.①②两种抽样方法,这100个零件中每个被抽到的概率都是![]() ,③并非如此
,③并非如此
C.①③两种抽样方法,这100个零件中每个被抽到的概率都是![]() ,②并非如此
,②并非如此
D.采用不同的抽样方法,这100个零件中每个被抽到的概率各不相同
7.曲线y=x3在点P处的切线斜率为k,当k=3时的P点坐标为
A.(-2,-8) B.(-1,-1),(1,1)
C.(2,8) D.(-![]() ,-
,-![]() )
)
8.已知y=loga(2-ax)在[0,1]上是x的减函数,则a的取值范围是
A.(0,1) B.(1,2)
C.(0,2) D.[2,+∞![]()
9.已知lg3,lg(sinx-![]() ),lg(1-y)顺次成等差数列,则
),lg(1-y)顺次成等差数列,则
A.y有最小值![]() ,无最大值 B.y有最大值1,无最小值
,无最大值 B.y有最大值1,无最小值
C.y有最小值![]() ,最大值1 D.y有最小值-1,最大值1
,最大值1 D.y有最小值-1,最大值1
10.若![]() =a,
=a,![]() =b,则∠AOB平分线上的向量
=b,则∠AOB平分线上的向量![]() 为
为
A.![]() B.
B.![]() (
(![]() ),
),![]() 由
由![]() 决定
决定
C.![]() D.
D.![]()
11.一对共轭双曲线的离心率分别是e1和e2,则e1+e2的最小值为
A.![]() B.2
B.2
C.2![]() D.4
D.4
12.式子![]() 的值为
的值为
A.0 B.1
C.2 D.3
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)
13.从A={a1,a2,a3,a4}到B={b1,b2,b3,b4}的一一映射中,限定a1的象不能是b1,且b4的原象不能是a4的映射有___________个.
14.椭圆5x2-ky2=5的一个焦点是(0,2),那么k=___________.
15.已知无穷等比数列首项为2,公比为负数,各项和为S,则S的取值范围为___________.
16.已知an是(1+x)n的展开式中x2的系数,则![]() =___________.
=___________.
参考答案
一、选择题(每小题5分,共60分)
B D C C D A B B A B C C
二、填空题(每小题4分,共16分)
14 ,-1 , 1<S<2, 2
三基小题训练十
命题:王统好
一选择题、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.(理)全集设为U,P、S、T均为U的子集,若![]() (
(![]()
![]() )=(
)=(![]()
![]() )
)![]() 则( )
则( )
A.![]() B.P=T=S C.T=U D.
B.P=T=S C.T=U D.![]()
![]()
![]() =T
=T
(文)设集合![]() ,
,![]() ,若U=R,且
,若U=R,且![]()
![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.m<2 B.m≥2 C.m≤2 D.m≤2或m≤-4
2.(理)复数![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)点M(8,-10),按a平移后的对应点![]() 的坐标是(-7,4),则a=( )
的坐标是(-7,4),则a=( )
A.(1,-6) B.(-15,14) C.(-15,-14) D.(15,-14)
3.已知数列![]() 前n项和为
前n项和为![]() ,则
,则![]() 的值是( )
的值是( )
A.13 B.-76 C.46 D.76
4.若函数![]() 的递减区间为(
的递减区间为(![]() ,
,![]() ),则a的取值范围是( )
),则a的取值范围是( )
A.a>0 B.-1<a<0 C.a>1 D.0<a<1
5.与命题“若![]() 则
则![]() ”的等价的命题是( )
”的等价的命题是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
6.(理)在正方体![]() 中,M,N分别为棱
中,M,N分别为棱![]() 和
和![]() 之中点,则sin(
之中点,则sin(![]() ,
,![]() )的值为( )
)的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)已知三棱锥S-ABC中,SA,SB,SC两两互相垂直,底面ABC上一点P到三个面SAB,SAC,SBC的距离分别为![]() ,1,
,1,![]() ,则PS的长度为( )
,则PS的长度为( )
A.9 B.![]() C.
C.![]() D.3
D.3
7.在含有30个个体的总体中,抽取一个容量为5的样本,则个体a被抽到的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(理)已知抛物线C:![]() 与经过A(0,1),B(2,3)两点的线段AB有公共点,则m的取值范围是( )
与经过A(0,1),B(2,3)两点的线段AB有公共点,则m的取值范围是( )
A.![]() ,
,![]()
![]() [3,
[3,![]() B.[3,
B.[3,![]() C.
C.![]() ,
,![]() D.[-1,3]
D.[-1,3]
(文)设![]() ,则函数
,则函数![]() 的图像在x轴上方的充要条件是( )
的图像在x轴上方的充要条件是( )
A.-1<x<1 B.x<-1或x>1
C.x<1 D.-1<x<1或x<-1
9.若直线y=kx+2与双曲线![]() 的右支交于不同的两点,则k的取值范围是( )
的右支交于不同的两点,则k的取值范围是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
10.a,b,c![]() (0,+∞)且表示线段长度,则a,b,c能构成锐角三角形的充要条件是( )
(0,+∞)且表示线段长度,则a,b,c能构成锐角三角形的充要条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.今有命题p、q,若命题S为“p且q”则“![]() 或
或![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
12.(理)函数![]() 的值域是( )
的值域是( )
A.[1,2] B.[0,2] C.(0,![]() D.
D.![]() ,
,![]()
(文)函数![]() 与
与![]() 图像关于直线x-y=0对称,则
图像关于直线x-y=0对称,则![]() 的单调增区间是( )
的单调增区间是( )
A.(0,2) B.(-2,0) C.(0,+∞) D.(-∞,0)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.等比数列![]() 的前n项和为
的前n项和为![]() ,且某连续三项正好为等差数列
,且某连续三项正好为等差数列![]() 中的第1,5,6项,则
中的第1,5,6项,则![]() ________.
________.
14.若![]() ,则k=________.
,则k=________.
15.有30个顶点的凸多面体,它的各面多边形内角总和是________.
16.长为l![]() 0<l<1
0<l<1![]() 的线段AB的两个端点在抛物线
的线段AB的两个端点在抛物线![]() 上滑动,则线段AB中点M到x轴距离的最小值是________.
上滑动,则线段AB中点M到x轴距离的最小值是________.
参考答案
1.(理)A (文)B 2.(理)B (文)B 3.B 4.A 5.D
6.(理)B (文)D 7.B 8.(理)C (文)D 9.D 10.D 11.C
12.(理)A (文)A 13.1或0 14.![]() 15.10080° 16.
15.10080° 16.![]()
三基小题训练十一
命题:王统好
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.已知a>b>0,全集为R,集合![]() ,
,![]() ,
,![]() ,则有( )
,则有( )
A.![]() (
(![]()
![]() ) B.
) B.![]() (
(![]()
![]() )
)![]() C.
C.![]() D.
D.![]()
2.已知实数a,b均不为零,![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知函数![]() 的图像关于点(-1,0)对称,且当
的图像关于点(-1,0)对称,且当![]() (0,+∞)时,
(0,+∞)时,![]() ,则当
,则当![]() (-∞,-2)时
(-∞,-2)时![]() 的解析式为( )
的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知![]() 是第三象限角,
是第三象限角,![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(理)已知抛物线![]() 上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点( )
上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点( )
A.(2,5) B.(-2,5) C.(5,-2) D.(5,2)
(文)过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 、
、![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 等于( )
等于( )
A.4p B.5p C.6p D.8p
6.设a,b,c是空间三条直线,![]() ,
,![]() 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )
A.当c⊥![]() 时,若c⊥
时,若c⊥![]() ,则
,则![]() ∥
∥![]()
B.当![]() 时,若b⊥
时,若b⊥![]() ,则
,则![]()
C.当![]() ,且c是a在
,且c是a在![]() 内的射影时,若b⊥c,则a⊥b
内的射影时,若b⊥c,则a⊥b
D.当![]() ,且
,且![]() 时,若c∥
时,若c∥![]() ,则b∥c
,则b∥c
7.两个非零向量a,b互相垂直,给出下列各式:
①a·b=0;
②a+b=a-b; ③a+b=a-b;
④a![]() +b
+b![]() =
=![]() a+b
a+b![]() ; ⑤(a+b)·(a-b)=0.
; ⑤(a+b)·(a-b)=0.
其中正确的式子有( )
A.2个 B.3个 C.4个 D.5个
8.已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,现从前m项:
,现从前m项:![]() ,
,![]() ,…,
,…,![]() 中抽出一项(不是
中抽出一项(不是![]() ,也不是
,也不是![]() ),余下各项的算术平均数为37,则抽出的是( )
),余下各项的算术平均数为37,则抽出的是( )
A.第6项 B.第8项 C.第12项 D.第15项
9.已知双曲线![]() (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为![]() 、
、![]() ,点A在双曲线第一象限的图象上,若△
,点A在双曲线第一象限的图象上,若△![]() 的面积为1,且
的面积为1,且![]() ,
,![]() ,则双曲线方程为( )
,则双曲线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.(理)某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有( )
A.![]() 种 B.
种 B.![]() 种 C.
种 C.![]() 种 D.
种 D.![]() 种
种
(文)某师范大学的2名男生和4名女生被分配到两所中学作实习教师,每所中学分配1名男生和2名女生,则不同的分配方法有( )
A.6种 B.8种 C.12种 D.16种
12.已知![]() 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意![]() ,都有
,都有![]() ,当
,当![]() [4,6]时,
[4,6]时,![]() ,则函数
,则函数![]() 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数![]() 的值
的值![]() 为( )
为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.(理)已知复数![]() ,
,![]() ,则复数
,则复数![]() 的虚部等于________.
的虚部等于________.
(文)从某社区150户高收入家庭,360户中等收入家庭,90户低收入家庭中,用分层抽样法选出100户调查社会购买力的某项指标,则三种家庭应分别抽取的户数依次为________.
14.若实数a,b均不为零,且![]() ,则
,则![]() 展开式中的常数项等于________.
展开式中的常数项等于________.
15.代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时________.
16.给出下列4个命题:
①函数![]() 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:
②若函数![]() 的定义域是
的定义域是![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() (其中
(其中![]() );
);
④圆:![]() 上任意点M关于直线
上任意点M关于直线![]() 的对称点,
的对称点,![]() 也在该圆上.
也在该圆上.
填上所有正确命题的序号是________.
答案:
1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A
10.B 11.(理)A (文)C 12.B 13.(理)![]() (文)25,60,15
(文)25,60,15
14.-672 15.2.5小时 16.①,④
三基小题训练十二
命题:王统好
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.满足条件![]()
![]() M
M![]() {0,1,2}的集合共有( )
{0,1,2}的集合共有( )
A.3个 B.6个 C.7个 D.8个
2.(文)等差数列![]() 中,若
中,若![]() ,
,![]() ,则前9项的和
,则前9项的和![]() 等于( )
等于( )
A.66 B.99 C.144 D.297
(理)复数![]() ,
,![]() ,则
,则![]() 的复平面内的对应点位于( )
的复平面内的对应点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.函数![]() 的反函数图像是( )
的反函数图像是( )
A B
C D
4.已知函数![]() 为奇函数,则
为奇函数,则![]() 的一个取值为( )
的一个取值为( )
A.0 B.![]() C.
C.![]() D.
D.![]()
5.从10种不同的作物种子中选出6种放入6个不同的瓶子中展出,如果甲、乙两种种子不能放入第1号瓶内,那么不同的放法共有( )
A.![]() 种 B.
种 B.![]() 种
种
C.![]() 种 D.
种 D.![]() 种
种
6.函数![]() 在[0,3]上的最大值、最小值分别是( )
在[0,3]上的最大值、最小值分别是( )
A.5,-15 B.5,-4
C.-4,-15 D.5,-16
7.(文)已知![]() 展开式的第7项为
展开式的第7项为![]() ,则实数x的值是( )
,则实数x的值是( )
A.![]() B.-3 C.
B.-3 C.![]() D.4
D.4
(理)已知![]() 展开式的第7项为
展开式的第7项为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.过球面上三点A、B、C的截面和球心的距离是球半径的一半,且AB=6,BC=8,AC=10,则球的表面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.给出下面四个命题:①“直线a、b为异面直线”的充分非必要条件是:直线a、b不相交;②“直线l垂直于平面![]() 内所有直线”的充要条件是:l⊥平面
内所有直线”的充要条件是:l⊥平面![]() ;③“直线a⊥b”的充分非必要条件是“a垂直于b在平面
;③“直线a⊥b”的充分非必要条件是“a垂直于b在平面![]() 内的射影”;④“直线
内的射影”;④“直线![]() ∥平面
∥平面![]() ”的必要非充分条件是“直线a至少平行于平面
”的必要非充分条件是“直线a至少平行于平面![]() 内的一条直线”.其中正确命题的个数是( )
内的一条直线”.其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
10.若0<a<1,且函数![]() ,则下列各式中成立的是( )
,则下列各式中成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.如果直线y=kx+1与圆![]() 交于M、N两点,且M、N关于直线x+y=0对称,则不等式组:
交于M、N两点,且M、N关于直线x+y=0对称,则不等式组: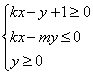 表示的平面区域的面积是( )
表示的平面区域的面积是( )
A.![]() B.
B.![]() C.1 D.2
C.1 D.2
12.九0年度大学学科能力测验有12万名学生,各学科成绩采用15级分,数学学科能力测验成绩分布图如下图:请问有多少考生的数学成绩分高于11级分?选出最接近的数目( )
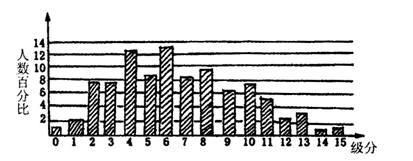
A.4000人 B.10000人
C.15000人 D.20000人
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.已知:![]() =2,
=2,![]() =
=![]() ,
,![]() 与
与![]() 的夹角为45°,要使
的夹角为45°,要使![]() 与
与![]() 垂直,则
垂直,则![]() __________.
__________.
14.若圆锥曲线![]() 的焦距与k无关,则它的焦点坐标是__________.
的焦距与k无关,则它的焦点坐标是__________.
15.定义符号函数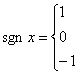
![]() ,则不等式:
,则不等式:![]() 的解集是__________.
的解集是__________.
16.若数列![]() ,
,![]() 是等差数列,则有数列
是等差数列,则有数列![]() 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列![]() 是等比数列,且
是等比数列,且![]() ,则有
,则有![]() __________
__________![]() 也是等比数列.
也是等比数列.
答案:
1.B 2.(文)B (理)D 3.C 4.B 5.C 6.A 7.(文)A (理)D
8.D 9.B 10.D 11.A 12.B 13.2
14.(0,![]() ) 15.
) 15.![]() 16.
16.![]()
三基小题训练十三
命题:王统好
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.(理)全集设为U,P、S、T均为U的子集,若![]() (
(![]()
![]() )=(
)=(![]()
![]() )
)![]() 则( )
则( )
A.![]() B.P=T=S
B.P=T=S
C.T=U D.![]()
![]()
![]() =T
=T
(文)设集合![]() ,
,![]() ,若U=R,且
,若U=R,且![]()
![]() ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.m<2 B.m≥2
C.m≤2 D.m≤2或m≤-4
2.(理)复数![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(文)点M(8,-10),按a平移后的对应点![]() 的坐标是(-7,4),则a=( )
的坐标是(-7,4),则a=( )
A.(1,-6) B.(-15,14)
C.(-15,-14) D.(15,-14)
3.已知数列![]() 前n项和为
前n项和为![]() ,则
,则![]() 的值是( )
的值是( )
A.13 B.-76 C.46 D.76
4.若函数![]() 的递减区间为(
的递减区间为(![]() ,
,![]() ),则a的取值范围是( )
),则a的取值范围是( )
A.a>0 B.-1<a<0
C.a>1 D.0<a<1
5.与命题“若![]() 则
则![]() ”的等价的命题是( )
”的等价的命题是( )
A.若![]() ,则
,则![]() B.若
B.若![]() ,则
,则![]()
C.若![]() ,则
,则![]() D.若
D.若![]() ,则
,则![]()
6.(理)在正方体![]() 中,M,N分别为棱
中,M,N分别为棱![]() 和
和![]() 之中点,则sin(
之中点,则sin(![]() ,
,![]() )的值为( )
)的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(文)已知三棱锥S-ABC中,SA,SB,SC两两互相垂直,底面ABC上一点P到三个面SAB,SAC,SBC的距离分别为![]() ,1,
,1,![]() ,则PS的长度为( )
,则PS的长度为( )
A.9 B.![]() C.
C.![]() D.3
D.3
7.在含有30个个体的总体中,抽取一个容量为5的样本,则个体a被抽到的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.(理)已知抛物线C:![]() 与经过A(0,1),B(2,3)两点的线段AB有公共点,则m的取值范围是( )
与经过A(0,1),B(2,3)两点的线段AB有公共点,则m的取值范围是( )
A.![]() ,
,![]()
![]() [3,
[3,![]() B.[3,
B.[3,![]()
C.![]() ,
,![]() D.[-1,3]
D.[-1,3]
(文)设![]() ,则函数
,则函数![]() 的图像在x轴上方的充要条件是( )
的图像在x轴上方的充要条件是( )
A.-1<x<1 B.x<-1或x>1
C.x<1 D.-1<x<1或x<-1
9.若直线y=kx+2与双曲线![]() 的右支交于不同的两点,则k的取值范围是( )
的右支交于不同的两点,则k的取值范围是( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
10.a,b,c![]() (0,+∞)且表示线段长度,则a,b,c能构成锐角三角形的充要条件是( )
(0,+∞)且表示线段长度,则a,b,c能构成锐角三角形的充要条件是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.今有命题p、q,若命题S为“p且q”则“![]() 或
或![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
12.(理)函数![]() 的值域是( )
的值域是( )
A.[1,2] B.[0,2]
C.(0,![]() D.
D.![]() ,
,![]()
(文)函数![]() 与
与![]() 图像关于直线x-y=0对称,则
图像关于直线x-y=0对称,则![]() 的单调增区间是( )
的单调增区间是( )
A.(0,2) B.(-2,0)
C.(0,+∞) D.(-∞,0)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.等比数列![]() 的前n项和为
的前n项和为![]() ,且某连续三项正好为等差数列
,且某连续三项正好为等差数列![]() 中的第1,5,6项,则
中的第1,5,6项,则![]() ________.
________.
14.若![]() ,则k=________.
,则k=________.
15.有30个顶点的凸多面体,它的各面多边形内角总和是________.
16.长为l![]() 0<l<1
0<l<1![]() 的线段AB的两个端点在抛物线
的线段AB的两个端点在抛物线![]() 上滑动,则线段AB中点M到x轴距离的最小值是________.
上滑动,则线段AB中点M到x轴距离的最小值是________.
答案:
1.(理)A (文)B 2.(理)B (文)B 3.B 4.A 5.D
6.(理)B (文)D 7.B 8.(理)C (文)D 9.D 10.D 11.C
12.(理)A (文)A 13.1或0 14.![]() 15.10080° 16.
15.10080° 16.![]()
三基小题训练十四
命题:王统好
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.已知a>b>0,全集为R,集合![]() ,
,![]() ,
,![]() ,则有( )
,则有( )
A.![]() (
(![]()
![]() ) B.
) B.![]() (
(![]()
![]() )
)![]()
C.![]() D.
D.![]()
2.已知实数a,b均不为零,![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知函数![]() 的图像关于点(-1,0)对称,且当
的图像关于点(-1,0)对称,且当![]() (0,+∞)时,
(0,+∞)时,![]() ,则当
,则当![]() (-∞,-2)时
(-∞,-2)时![]() 的解析式为( )
的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知![]() 是第三象限角,
是第三象限角,![]() ,且
,且![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.(理)已知抛物线![]() 上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点( )
上两个动点B、C和点A(1,2)且∠BAC=90°,则动直线BC必过定点( )
A.(2,5) B.(-2,5) C.(5,-2) D.(5,2)
(文)过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 、
、![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 等于( )
等于( )
A.4p B.5p C.6p D.8p
6.设a,b,c是空间三条直线,![]() ,
,![]() 是空间两个平面,则下列命题中,逆命题不成立的是( )
是空间两个平面,则下列命题中,逆命题不成立的是( )
A.当c⊥![]() 时,若c⊥
时,若c⊥![]() ,则
,则![]() ∥
∥![]()
B.当![]() 时,若b⊥
时,若b⊥![]() ,则
,则![]()
C.当![]() ,且c是a在
,且c是a在![]() 内的射影时,若b⊥c,则a⊥b
内的射影时,若b⊥c,则a⊥b
D.当![]() ,且
,且![]() 时,若c∥
时,若c∥![]() ,则b∥c
,则b∥c
7.两个非零向量a,b互相垂直,给出下列各式:
①a·b=0;
②a+b=a-b;
③a+b=a-b;
④a![]() +b
+b![]() =
=![]() a+b
a+b![]() ;
;
⑤(a+b)·(a-b)=0.
其中正确的式子有( )
A.2个 B.3个 C.4个 D.5个
8.已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,现从前m项:
,现从前m项:![]() ,
,![]() ,…,
,…,![]() 中抽出一项(不是
中抽出一项(不是![]() ,也不是
,也不是![]() ),余下各项的算术平均数为37,则抽出的是( )
),余下各项的算术平均数为37,则抽出的是( )
A.第6项 B.第8项
C.第12项 D.第15项
9.已知双曲线![]() (a>0,b>0)的两个焦点为
(a>0,b>0)的两个焦点为![]() 、
、![]() ,点A在双曲线第一象限的图象上,若△
,点A在双曲线第一象限的图象上,若△![]() 的面积为1,且
的面积为1,且![]() ,
,![]() ,则双曲线方程为( )
,则双曲线方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.在正三棱锥A-BCD中,E,F分别是AB,BC的中点,EF⊥DE,且BC=1,则正三棱锥A-BCD的体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.(理)某城市新修建的一条道路上有12盏路灯,为了节省用电而又不能影响正常的照明,可以熄灭其中的3盏灯,但两端的灯不能熄灭,也不能熄灭相邻的两盏灯,则熄灯的方法有( )
A.![]() 种 B.
种 B.![]() 种 C.
种 C.![]() 种 D.
种 D.![]() 种
种
(文)某师范大学的2名男生和4名女生被分配到两所中学作实习教师,每所中学分配1名男生和2名女生,则不同的分配方法有( )
A.6种 B.8种 C.12种 D.16种
12.已知![]() 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意![]() ,都有
,都有![]() ,当
,当![]() [4,6]时,
[4,6]时,![]() ,则函数
,则函数![]() 在区间[-2,0]上的反函数
在区间[-2,0]上的反函数![]() 的值
的值![]() 为( )
为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.(理)已知复数![]() ,
,![]() ,则复数
,则复数![]() 的虚部等于________.
的虚部等于________.
(文)从某社区150户高收入家庭,360户中等收入家庭,90户低收入家庭中,用分层抽样法选出100户调查社会购买力的某项指标,则三种家庭应分别抽取的户数依次为________.
14.若实数a,b均不为零,且![]() ,则
,则![]() 展开式中的常数项等于________.
展开式中的常数项等于________.
15.代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时________.
16.给出下列4个命题:
①函数![]() 是奇函数的充要条件是m=0:
是奇函数的充要条件是m=0:
②若函数![]() 的定义域是
的定义域是![]() ,则
,则![]() ;
;
③若![]() ,则
,则![]() (其中
(其中![]() );
);
④圆:![]() 上任意点M关于直线
上任意点M关于直线![]() 的对称点,
的对称点,![]() 也在该圆上.
也在该圆上.
填上所有正确命题的序号是________.
参考答案
1.A 2.B 3.B 4.D 5.(理)C (文)A 6.B 7.A 8.B 9.A
10.B 11.(理)A (文)C 12.B 13.(理)![]() (文)25,60,15
(文)25,60,15
14.-672 15.2.5小时 16.①,④
三基小题训练十五
命题:王统好
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.(文)已知命题甲为x>0;命题乙为![]() ,那么( )
,那么( )
A.甲是乙的充分非必要条件
B.甲是乙的必要非充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件,也不是乙的必要条件
(理)已知两条直线![]() ∶ax+by+c=0,直线
∶ax+by+c=0,直线![]() ∶mx+ny+p=0,则an=bm是直线
∶mx+ny+p=0,则an=bm是直线![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.(文)下列函数中,周期为![]() 的奇函数是( )
的奇函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(理)方程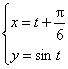 (t是参数,
(t是参数,![]() )表示的曲线的对称轴的方程是( )
)表示的曲线的对称轴的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.在复平面中,已知点A(2,1),B(0,2),C(-2,1),O(0,0).给出下面的结论:
①直线OC与直线BA平行; ②![]() ;
;
③![]() ;
④
;
④![]() .
.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
4.(文)在一个锥体中,作平行于底面的截面,若这个截面面积与底面面积之比为1∶3,则锥体被截面所分成的两部分的体积之比为( )
A.1∶![]() B.1∶9 C.1∶
B.1∶9 C.1∶![]() D.1∶
D.1∶![]()
(理)已知数列![]() 的通项公式是
的通项公式是![]() ,其中a、b均为正常数,那么
,其中a、b均为正常数,那么![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]()
C.![]() D.与n的取值相关
D.与n的取值相关
5.(文)将4张互不相同的彩色照片与3张互不相同的黑白照片排成一排,任何两张黑白照片都不相邻的不同排法的种数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量
| 单价 (元/kg) | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量 (1000kg) | 50 | 60 | 70 | 75 | 80 | 90 |
表2 市场需求量
| 单价 (元/kg) | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量 (1000kg) | 50 | 60 | 65 | 70 | 75 | 80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间( )
A.(2.3,2.6)内 B.(2.4,2.6)内
C.(2.6,2.8)内 D.(2.8,2.9)内
6.椭圆![]() 的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
的焦点在y轴上,长轴长是短轴长的两倍,则m的值为( )
A.![]() B.
B.![]() C.2 D.4
C.2 D.4
7.若曲线![]() 在点P处的切线平行于直线3x-y=0,则点P的坐标为( )
在点P处的切线平行于直线3x-y=0,则点P的坐标为( )
A.(1,3) B.(-1,3)
C.(1,0) D.(-1,0)
8.已知函数![]() 是R上的偶函数,且在(-∞,
是R上的偶函数,且在(-∞,![]() 上是减函数,若
上是减函数,若![]() ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.a≤2 B.a≤-2或a≥2
C.a≥-2 D.-2≤a≤2
9.如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
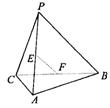
A.60° B.45° C.0° D.120°
10.圆心在抛物线![]() 上,并且与抛物线的准线及x轴都相切的圆的方程是( )
上,并且与抛物线的准线及x轴都相切的圆的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
11.双曲线的虚轴长为4,离心率![]() ,
,![]() 、
、![]() 分别是它的左、右焦点,若过
分别是它的左、右焦点,若过![]() 的直线与双曲线的右支交于A、B两点,且
的直线与双曲线的右支交于A、B两点,且![]() 是
是![]() 的等差中项,则
的等差中项,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.8.
D.8.
12.如图,在正方形ABCD中,E、F、G、H是各边中点,O是正方形中心,在A、E、B、F、C、G、D、H、O这九个点中,以其中三个点为顶点作三角形,在这些三角形中,互不全等的三角形共有( )
A.6个 B.7个 C.8个 D.9个
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.若![]() 是数列
是数列![]() 的前n项的和,
的前n项的和,![]() ,则
,则![]() ________.
________.
14.若x、y满足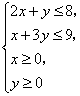 则
则![]() 的最大值为________.
的最大值为________.
15.有A、B、C、D、E五名学生参加网页设计竞赛,决出了第一到第五的名次,A、B两位同学去问成绩,教师对A说:“你没能得第一名”.又对B说:“你得了第三名”.从这个问题分析,这五人的名次排列共有________种可能(用数字作答).
16.若对n个向量![]() ,…,
,…,![]() 存在n个不全为零的实数
存在n个不全为零的实数![]() ,
,![]() ,…,
,…,![]() ,使得
,使得![]() 成立,则称向量
成立,则称向量![]() ,
,![]() ,…,
,…,![]() 为“线性相关”.依此规定,能说明
为“线性相关”.依此规定,能说明![]() (1,2),
(1,2),![]() (1,-1),
(1,-1),![]() (2,2)“线性相关”的实数
(2,2)“线性相关”的实数![]() ,
,![]() ,
,![]() 依次可以取________(写出一组数值即中,不必考虑所有情况).
依次可以取________(写出一组数值即中,不必考虑所有情况).
参考答案
1.(文)A(理)C 2.(文)A(理)B 3.C 4.(文)D(理)B
5.(文)D (理)C 6.A 7.C 8.B 9.A 10.D 11.A 12.C
13.33 14.7 15.18
16.只要写出-4c,2c,c(c≠0)中一组即可,如-4,2,1等
三基小题训练十六
命题:王统好
一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的.
1.两个非零向量e![]() ,e
,e![]() 不共线,若(ke
不共线,若(ke![]() +e
+e![]() )∥(e
)∥(e![]() +ke
+ke![]() ),则实数k的值为( )
),则实数k的值为( )
A.1 B.-1 C.±1 D.0
2.有以下四个命题,其中真命题为( )
A.原点与点(2,3)在直线2x+y-3=0的同侧
B.点(2,3)与点(3,1)在直线x-y=0的同侧
C.原点与点(2,1)在直线2y-6x+1=0的异侧
D.原点与点(2,1)在直线2y-6x+1=0的同侧
3.①某高校为了解学生家庭经济收入情况,从来自城镇的150名学生和来自农村的150名学生中抽取100名学生的样本;②某车间主任从100件产品中抽取10件样本进行产品质量检验.
I.随机抽样法;Ⅱ.分层抽样法.
上述两问题和两方法配对正确的是( )
A.①配I,②配Ⅱ B.①配Ⅱ,②配Ⅰ
C.①配I,②配I D.①配Ⅱ,②配Ⅱ
4.已知函数![]() ,其反函数为
,其反函数为![]() ,则
,则![]() 是( )
是( )
A.奇函数且在(0,+∞)上单调递减
B.偶函数且在(0,+∞)上单调递增
C.奇函数且在(-∞,0)上单调递减
D.偶函数且在(-∞,0)上单调递增
5.以下四个命题:
①过一点有且仅有一个平面与已知直线垂直;
②若平面外两点到平面的距离相等,则过这两点的直线必平行于该平面;
③两条相交直线在同一平面内的射影必为相交直线;
④两个互相垂直的平面,一个平面内的任一直线必垂直于另一平面的无数条直线.
其中正确的命题是( )
A.①和② B.②和③ C.③和④ D.①和④
6.从单词“education”中选取5个不同的字母排成一排,则含“at”(“at”相连且顺序不变)的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知正二十面体的各面都是正三角形,那么它的顶点数为( )
A.30 B.12 C.32 D.10
8.已知![]() 的展开式中,
的展开式中,![]() 系数为56,则实数a的值为( )
系数为56,则实数a的值为( )
A.6或5 B.-1或4
C.6或-1 D.4或5
9.对某种产品市场产销量情况如图所示,其中:![]() 表示产品各年年产量的变化规律;
表示产品各年年产量的变化规律;![]() 表示产品各年的销售情况.下列叙述:
表示产品各年的销售情况.下列叙述:
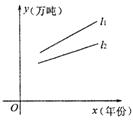
(1)产品产量、销售量均以直线上升,仍可按原生产计划进行下去;
(2)产品已经出现了供大于求的情况,价格将趋跌;
(3)产品的库存积压将越来越严重,应压缩产量或扩大销售量;
(4)产品的产、销情况均以一定的年增长率递增.你认为较合理的是( )
A.(1),(2),(3) B.(1),(3),(4)
C.(2),(4) D.(2),(3)
10.(文)函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理)函数![]() 是( )
是( )
A.周期为![]() 的偶函数 B.周期为
的偶函数 B.周期为![]() 的奇函数
的奇函数
C.周期为2![]() 的偶函数 D.周期为2
的偶函数 D.周期为2![]() 的奇函数
的奇函数
11.(文)如图,正四面体ABCD中,E为AB中点,F为CD的中点,则异面直线EF与SA所成的角为( )
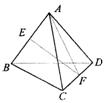
A.90° B.60° C.45° D.30°
(理)如图,正三棱柱![]() 中,AB=
中,AB=![]() ,则
,则![]() 与平面
与平面![]() 所成的角的正弦值为( )
所成的角的正弦值为( )
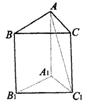
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.(文)抛物线![]() 的焦点在x轴上,则实数m的值为( )
的焦点在x轴上,则实数m的值为( )
A.0
B.![]() C.2 D.3
C.2 D.3
(理)已知椭圆![]() (a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
(a>0)与A(2,1),B(4,3)为端点的线段没有公共点,则a的取值范围是( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
二、填空题:本题共4小题,共16分,把答案填在题中的横线上
13.已知a=(3,4),a-b=1,则b的范围是________.
14.已知直线y=x+1与椭圆![]() (m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于
(m>n>0)相交于A,B两点,若弦AB的中点的横坐标等于![]() ,则双曲线
,则双曲线![]() 的两条渐近线的夹角的正切值等于________.
的两条渐近线的夹角的正切值等于________.
15.某县农民均收入服从![]() =500元,
=500元,![]() =20元的正态分布,则此县农民年均收入在500元到520元间人数的百分比为________.
=20元的正态分布,则此县农民年均收入在500元到520元间人数的百分比为________.
16.![]() =________.
=________.
参考答案
1.C 2.C 3.B 4.D 5.D 6.A 7.B 8.C 9.D
10.(文)B (理)B 11.(文)C (理)C 12.(文)B (理)B 13.[4,6]
14.![]() 15.34.15% 16.
15.34.15% 16.![]()
三基小题训练十七
命题:王统好
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.sin2·cos3·tg4的值( )
A.小于0 B.大于0 C.等于0 D.不存在
2.直线y=ax+b通过一、三、四象限,则圆(x+a)2+(y+b)2=r2(r>0)的圆心位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.数列{an}是等差数列的一个充要条件是( )
A.Sn=an+b B.Sn=an2+bn+c
C.Sn=an2+bn(a≠0) D.Sn=an2+bn
4.若函数f (x)=logx2在(0,∞)上是减函数,则a的取值范围是( )
A.a>1 B.a< C.a> D.1<a<
5.在极坐标系中,已知点P(1,),下列各点中与点P重合的共有( )
①(-1,π) ②(1,-) ③(-1,) ④(1,-π)
A.1个 B.2个 C.3个 D.4个
6.y=arc cos(2x-1)的反函数是( )
A.y=+arc cos2x x∈[-,] B.y=+cos2x x∈[-,]
C.y=+arc cos2x x∈[0,] D.y=+cos2x x∈[0,]
7.已知椭圆+=1(a>b>0),直线l:y=x+t交椭圆于A、B两点,△OAB的面积为S(O为原点),则函数S=f ( t )的奇偶性为( )
A.奇函数 B.偶函数
C.不是奇函数,也不是偶函数 D.奇偶性与a、b有关
8.设p=cosα·cosβ,q=cos2 ,那么p、q的大小关系是( )
A.p>q B.p<q C.p≤q D.p≥q
9.等边△ABC的边长为a,过△ABC的中心O作OP⊥平面ABC,且OP=a,则点P到△ABC的边的距离为( )
A.a B.a C.a D.a
10.已知函数f (x)是定义域为R的奇函数,给出下列6个函数:
①g (x)=;②g (x)=sin(π+x);③g (x)=;
④g (x)=lg sin x ;⑤g (x)=lg(+x);⑥g (x)=-1。
其中可以使函数F(x)=f (x)·g (x)是偶函数的函数是( )
A.①⑥ B.①⑤ C.⑤⑥ D.③⑤
11.已知半圆x2+y2=4(y<0)上任一点P(t,h)过点P作切线,切线的斜率为k,则函数k=f (t)的单调性为( )
A.增函数 B.减函数 C.先增后减 D.先减后增
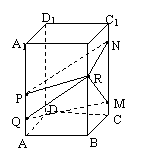
 12.如图是一人出差从A城出发到B城去,
D1
12.如图是一人出差从A城出发到B城去,
D1
沿途可能经过的城市的示意图,通过两城市所 C1 E1
需时间标在两城市之间的连线上(单位:小时), A D2 B
则此人从A城出发到B城所需时间最少为( ) C2 E2
A.49小时 B.46小时 D3
C.48小时 D.47小时 12题图
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:(本大题共4小题,每小题4分,共16分,把答案填在题中横线上。)
13.已知圆x2+y2+mx-7=0与抛物线x2=4(y+3)的准线相切,则m=______.
14.对于实数a、b、c、d,定义运算“⊙”:(a,b)⊙(c,d)=(ac-bd,ad+bc),那么,(0,1)⊙(0,1)=_________.
15.4个相同的白球和3个相同的黑球,随机地排成一行,不同的排法有m种,其中有且仅有2个黑球相邻的排法为n种,则=______.(用数字作答)
16.设an是(3-)n的展开式中x项的系数(n=2,3,4,…),则(++…+)=________.
参考答案及评分标准
一、选择题
1.A 2.B 3.D 4.D 5.B 6.D 7.B 8.C 9.B 10.C 11.A 12.C
二、填空题
13.±6 14.(-1,0) 15.4/7 16.18
三基小题训练十八
命题:王统好
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设p、q是两个命题,则“复合命题p或q为真,p且q为假”的充要条件是 ( )
A.p、q中至少有一个为真 B.p、q中至少有一个为假
C.p、q中中有且只有一个为真 D.p为真,q为假
2.已知复数![]() ( )
( )
A.![]() B.2 C.2
B.2 C.2![]() D.8
D.8
3.已知a、b、c是三条互不重合的直线,α、β是两个不重合的平面,给出四个命题:
①![]() ②a、
②a、![]() ③
③![]() ④
④![]() .其中正确命题的个数是 ( )
.其中正确命题的个数是 ( )
A.1个 B.2个 C.3个 D.4个
4.已知等差数列![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.定义在R上的偶函数![]() 的x的集合为 ( )
的x的集合为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
|
A.![]() B.1
B.1
C.6 D.3
7.已知函数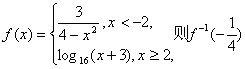 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.4 D.-4
C.4 D.-4
8.若半径为R的球与正三棱柱的各个面都相切,则球与正三棱柱的体积比为 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.如果以原点为圆心的圆经过双曲线![]() 的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于 ( )
的焦点,而且被该双曲线的右准线分成弧长为2:1的两段圆弧,那么该双曲线的离心率e等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
A.![]() B.
B.![]()
|
11.若函数![]() 的图象如右图所示,则
的图象如右图所示,则
函数![]() 的图象大致为( )
的图象大致为( )
|
A B C D
12.已知函数![]() 有以下四个函数:①
有以下四个函数:①![]() ②
②![]() ③
③![]()
④![]()
其中满足f (x)所有条件的函数序号为 ( )
A.①② B.②③ C.②④ D.①④
|
13.![]() 展开式中的常数项为
.
展开式中的常数项为
.
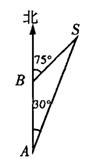
14.如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8![]() n mile.此船的航速是
n mile/h.
n mile.此船的航速是
n mile/h.
|
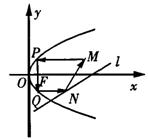
16.如图,从点![]() 发出的光线沿平行于抛物线
发出的光线沿平行于抛物线![]() 的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线
的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线![]() 再反射后又射回点M,则
再反射后又射回点M,则
x0= .
答案:
一、选择题:本题考查基本知识和基本运算,每小题5分,满分60分.
1.C 2.C 3.B 4.D 5.D 6.B 7.D 8.B 9.D 10.A 11.A 12.B
二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分.
13.![]() 14.32 15.16 16.6
14.32 15.16 16.6
三基小题训练十九
命题:王统好
一、选择题:(每题5分,共50分,单选题)
1.已知集合P={-2,-1,0,1,2,3},集合Q={x∈R![]() },则P∩Q等于
},则P∩Q等于
(A){-2,-1,0,1} (B){-1,0,1 }
(C){-1,0,1,2} (D){-1,0,1,2,3}
2.“所有的函数都是连续的”的否命题是
(A)某些函数不是连续的 (B)所有的函数都不是连续的
(C)没有函数是连续的 (D)没有函数不是连续的
3.正方体的全面积为24,球O与正方体的各棱均相切,球O的体积是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4. 已知圆O的半径为![]() ,圆周上两点A、B与原点O恰构成正三角形,向量
,圆周上两点A、B与原点O恰构成正三角形,向量![]() 的数量积是
的数量积是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.已知空间中两条不重合的直线a和b互相垂直,它们在同一平面α上的射影不可能是下面哪一种情况?
(A)两条平行直线 (B)一条直线及这条直线外一点
(C)两条相交成45°角的直线 (D)两个点
6.函数y=sinx的图象按向量a=(![]() ,2)平移后与函数g(x)的图象重合,则
,2)平移后与函数g(x)的图象重合,则
g(x)的函数表达式是
(A)cosx-2 (B)-cosx-2 (C)cosx+2 (D)-cosx+2
7.将等差数列1,4,7,10,…中的各项,按如下方式分组(按原来的次序,每组中的项数成等比数列):1,(4,7),(10,13,16,19),(22,25,28,31,34,37,40,43),….则2005在第几组中?
(A)第9组 (B)第10组 (C)第11组 (D)第12组
8.动点P在抛物线y2=-6x上运动,定点A(0,1),线段PA中点的轨迹方程是. ![]()
(A)(2y+1)2=-12x (B)(2y+1)2=12x
(C)(2y-1)2=-12x (D)(2y-1)2=12x
9.在一次数学实验中, 运用图形计算器采集到如下一组数据.
| x | -2.0 | -1.0 | 0 | 1.00 | 2.00 | 3.00 |
| y | 0.24 | 0.51 | 1 | 2.02 | 3.98 | 8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)
(A)y=a+bX (B)y=a+bx (C)y=a+logbx (D)y=a+b/x
10.方程![]() 表示的曲线所围成区域的面积是
表示的曲线所围成区域的面积是
(A)6 (B)12 (C)24 (D)48
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
11. 已知![]() ;
; ![]() = .
= .
12.将边长为1的正三角形ABC沿高AD折叠成直二面角B-AD-C,则直线AC与直线AB所成角的余弦值是
13.双曲线的焦点是F1、F2,P是双曲线上一点,P到双曲线两条准线的距离之比为5︰3,∠F1PF2=120°,则双曲线的离心率是
14.已知函数f(x)= 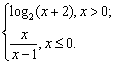 则f-1(
则f-1(![]() )= ;f(x)的反函数
.
)= ;f(x)的反函数
.
答案:
BADCD DBCAC
11.![]() ,
,![]() 12. 3/4 13. 7/2(或3.5 ) 14. -1;
12. 3/4 13. 7/2(或3.5 ) 14. -1;
三基小题训练二十
命题:王统好
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只
有一项是符合题目要求的。
1.
若![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.
![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.
不等式![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.
直线![]() 与圆
与圆![]() 相切,则常数
相切,则常数![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
5.
在![]() 中,“
中,“![]() ”是“
”是“![]() ”的( )
”的( )
A.充分而不必要条件 B.充要条件
C.必要而不充分条件 D.既不充分也不必要条件
6.
在等差数列![]() 中,
中,![]() ,
,![]() ,则此数列前
,则此数列前![]() 项的和等于:
项的和等于:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.
椭圆![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,且椭圆上的点
,且椭圆上的点![]() 满足
满足![]() ,则
,则![]() :
:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.
![]() 的展开式中的常数项是( )
的展开式中的常数项是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.
已知球的表面积为![]() ,
,![]() 、
、![]() 、
、![]() 三点都在球面上,且每两点间的球面距离均为
三点都在球面上,且每两点间的球面距离均为![]() ,则球心
,则球心![]() 到平面
到平面![]() 的距离为( )
的距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. 将![]() 名医生分配到
名医生分配到![]() 间医院,每间医院至少
间医院,每间医院至少![]() 名医生,则不同的分配方案共有( )
名医生,则不同的分配方案共有( )
A.![]() 种 B.
种 B.![]() 种 C.
种 C.![]() 种 D.
种 D.![]() 种
种
12. 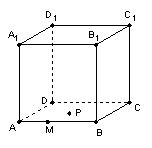 如图,正方体
如图,正方体![]() 的棱长为
的棱长为![]() ,点
,点![]() 在棱
在棱![]() 上,
上,
且![]() ,点
,点![]() 是平面
是平面![]() 上的动点,且动点
上的动点,且动点![]() 到直线
到直线
![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离的平方差为
的距离的平方差为![]() ,则动点
,则动点![]() 的
的
轨迹是( )
A.圆 B.抛物线 C.双曲线 D.直线
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。
13. 设复数![]() ,则
,则![]() 。
。
14. 某单位业务人员、管理人员、后勤服务人员人数之比依次为![]() 。为了了解该单位职员的某种情况,采用分层抽样方法抽出一个容量为
。为了了解该单位职员的某种情况,采用分层抽样方法抽出一个容量为![]() 的样本,样本中业务人员人数为
的样本,样本中业务人员人数为![]() ,则此样本的容量
,则此样本的容量![]() 。
。
15. 设![]() 、
、![]() 满足约束条件:
满足约束条件: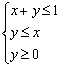 ,则
,则![]() 的最大值是 。
的最大值是 。
16. 已知![]() 、
、![]() 为不垂直的异面直线,
为不垂直的异面直线,![]() 是一个平面,则
是一个平面,则![]() 、
、![]() 在
在![]() 上的射影有可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点。在上面的结论中,正确结论的编号是 。(写出所有正确结论的序号)
上的射影有可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点。在上面的结论中,正确结论的编号是 。(写出所有正确结论的序号)
答案:
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | A | C | A | B | A | A | D | C | D | B |
二、填空题:
13.![]() 14.
14.![]() 15.
15.![]() 16.①②④
16.①②④
三基小题训练二十一
命题:王统好
一. 选择题 : 本大题共12小题, 每小题5分, 共60分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .
1.(理科)设z = ![]() , 则z2 等于 ( )
, 则z2 等于 ( )
(A) ![]() . (B)
. (B)
![]() .
(C)
.
(C) ![]() .
(D)
.
(D) ![]() .
.
(文科)sin600° = ( )
(A) –![]() (B)–
(B)–![]() .
(C)
.
(C)![]() .
(D)
.
(D) ![]() .
.
2.设A = { x x ³ 2}, B = { x x – 1< 3}, 则A∩B= ( )
(A)[2,4] (B)(–∞,–2]
(C)[–2,4] (D)[–2,+∞)
3.若a=2sin150,b=4cos150,a与b的夹角为300,则a·b的值为 ( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
4.△ABC中,角A、B、C所对的边分别为a、b、c,则acosC+ccosA的值为 ( )
(A)b. (B)![]() . (C)2cosB. (D)2sinB.
. (C)2cosB. (D)2sinB.
5.一个容量为20的样本数据,分组后,组距与频数如下:
| 组距 | (10 , 20] | (20 , 30] | (30 , 40] | (40 , 50] | (50 , 60] | (60 , 70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
则样本在(10 , 50]上的频率为 ( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
6.当x Î R时,令f (x )为sinx与cosx中的较大或相等者,设a £ f ( x ) £ b, 则a + b 等于 ( )
(A)0 (B) 1 + ![]() . (C)1–
. (C)1–![]() . (D)
. (D)![]() –1.
–1.
7.(理科)设f ( x ) = ax3 + bx2 + cx + d, a , b, c, d Î R, 又m , n ÎR , m < n,则下列正确的判断是 ( )
(A) 若f ( m )f ( n ) <0,则f ( x ) = 0在m , n之间只有一个实根
(B) 若f ( m ) f ( n ) > 0,则f ( x ) = 0在m, n之间至少有一个实根
(C) 若f ( x ) = 0在m , n之间至少有一个实根,则 f ( m ) f ( n ) < 0
(D) 若f ( m ) f ( n ) > 0, 则f ( x ) =0在m , n之间也可能有实根
(文科)函数![]() 在区间[0,1]上是( )
在区间[0,1]上是( )
(A)单调递增的函数. (B)单调递减的函数.
(C)先减后增的函数 . (D)先增后减的函数.
8.有80个数,其中一半是奇数,一半是偶数,从中任取两数,则所取的两数和为偶数的概率为 ( )
(A) ![]() . (B)
. (B)![]() . (C)
. (C) ![]() . (D)
. (D)![]() .
.
9.对于x∈[0,1]的一切值,a +2b > 0是使ax + b > 0恒成立的( )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
10.设{an}是等差数列,从{a1,a2,a3,··· ,a20}中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有( )
(A)90个 . (B)120个. (C)180个. (D)200个.
11.已知函数y = f ( x )(x∈R)满足f (x +1) = f ( x – 1),且x∈[–1,1]时,f (x) = x2,则y = f ( x ) 与y = log5x的图象的交点个数为 ( )
(A)1. (B)2 . (C)3 . (D)4.
12.给出下列命题:
(1) 若0< x <![]() , 则sinx < x < tanx .
, 则sinx < x < tanx .
(2) 若–![]() < x< 0, 则sin x < x < tanx.
< x< 0, 则sin x < x < tanx.
(3) 设A,B,C是△ABC的三个内角,若A > B > C, 则sinA > sinB > sinC.
(4) 设A,B是钝角△ABC的两个锐角,若sinA > sinB > sinC 则A > B > C..
其中,正确命题的个数是( )
(A) 4. (B)3. (C)2. (D)1.
二. 填空题: 本大题有4小题, 每小题4分, 共16分. 请将答案填写在题中的横线上.
13. ![]() 的展开式的第4项是 .
的展开式的第4项是 .
14. 某客运公司定客票的方法是:如果行程不超过100km,票价是0.5元/km, 如果超过100km, 超过100km部分按0.4元/km定价,则客运票价y元与行程公里数x km之间的函数关系式是 .
15.(理科)在ABC中,若:= = ,则COSA等于___________.
(文科)在边长为4的正三角形ABC中 =___________
16.(理科)已知f(x)是可导的偶函数,且=-2,则曲线f(x)在(-1,2)处的切线方程是________.
(文科)设P是曲线y = x2 – 1上的动点,O为坐标原点,当![]() 2取得最小值时,点P的坐标为
2取得最小值时,点P的坐标为
三基小题训练二十二
命题:王统好
一. 选择题 : 本大题共12小题, 每小题5分, 共60分. 在每小题给出的四个选项中, 有且只有一项是符合题目要求的 .
1.(理科)设z = ![]() , 则z2 等于 ( )
, 则z2 等于 ( )
(A) ![]() . (B)
. (B)
![]() .
(C)
.
(C) ![]() .
(D)
.
(D) ![]() .
.
(文科)sin600° = ( )
(A) –![]() (B)–
(B)–![]() .
(C)
.
(C)![]() .
(D)
.
(D) ![]() .
.
2.设A = { x x ³ 2}, B = { x x – 1< 3}, 则A∩B= ( )
(A)[2,4] (B)(–∞,–2]
(C)[–2,4] (D)[–2,+∞)
3.若a=2sin150,b=4cos150,a与b的夹角为300,则a·b的值为 ( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
4.△ABC中,角A、B、C所对的边分别为a、b、c,则acosC+ccosA的值为 ( )
(A)b. (B)![]() . (C)2cosB. (D)2sinB.
. (C)2cosB. (D)2sinB.
5.一个容量为20的样本数据,分组后,组距与频数如下:
| 组距 | (10 , 20) | (20 , 30] | (30 , 40] | (40 , 50] | (50 , 60] | (60 , 70] |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
则样本在(10 , 50]上的频率为 ( )
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
6.当x Î R时,令f (x )为sinx与cosx中的较大或相等者,设a £ f ( x ) £ b, 则a + b 等于 ( )
(A)0 (B) 1 + ![]() . (C)1–
. (C)1–![]() . (D)
. (D)![]() –1.
–1.
7.(理科)设f ( x ) = ax3 + bx2 + cx + d, a , b, c, d Î R, 又m , n ÎR , m < n,则下列正确的判断是 ( )
(A) 若f ( m )f ( n ) <0,则f ( x ) = 0在m , n之间只有一个实根
(B) 若f ( m ) f ( n ) > 0,则f ( x ) = 0在m, n之间至少有一个实根
(C) 若f ( x ) = 0在m , n之间至少有一个实根,则 f ( m ) f ( n ) < 0
(D) 若f ( m ) f ( n ) > 0, 则f ( x ) =0在m , n之间也可能有实根
(文科)函数![]() 在区间[0,1]上是( )
在区间[0,1]上是( )
(A)单调递增的函数. (B)单调递减的函数.
(C)先减后增的函数 . (D)先增后减的函数.
8.有80个数,其中一半是奇数,一半是偶数,从中任取两数,则所取的两数和为偶数的概率为 ( )
(A) ![]() . (B)
. (B)![]() . (C)
. (C) ![]() . (D)
. (D)![]() .
.
9.对于x∈[0,1]的一切值,a +2b > 0是使ax + b > 0恒成立的( )
(A)充要条件 (B)充分不必要条件
(C)必要不充分条件 (D)既不充分也不必要条件
10.设{an}是等差数列,从{a1,a2,a3,··· ,a20}中任取3个不同的数,使这三个数仍成等差数列,则这样不同的等差数列最多有( )
(A)90个 . (B)120个. (C)180个. (D)200个.
11.已知函数y = f ( x )(x∈R)满足f (x +1) = f ( x – 1),且x∈[–1,1]时,f (x) = x2,则y = f ( x ) 与y = log5x的图象的交点个数为 ( )
(A)1. (B)2 . (C)3 . (D)4.
12.给出下列命题:
(1) 若0< x <![]() , 则sinx < x < tanx .
, 则sinx < x < tanx .
(2) 若–![]() < x< 0, 则sin x < x < tanx.
< x< 0, 则sin x < x < tanx.
(3) 设A,B,C是△ABC的三个内角,若A > B > C, 则sinA > sinB > sinC.
(4) 设A,B是钝角△ABC的两个锐角,若sinA > sinB > sinC 则A > B > C..
其中,正确命题的个数是( )
(A) 4. (B)3. (C)2. (D)1.
二. 填空题: 本大题有4小题, 每小题4分, 共16分. 请将答案填写在题中的横线上.
13. ![]() 的展开式的第4项是 .
的展开式的第4项是 .
14. 某客运公司定客票的方法是:如果行程不超过100km,票价是0.5元/km, 如果超过100km, 超过100km部分按0.4元/km定价,则客运票价y元与行程公里数x km之间的函数关系式是 .
15. (理科) 在△ABC中,若![]() =
=![]() =
=![]() ,则cosA 等于_______________
.
,则cosA 等于_______________
.
三、
(文科)在边长为4的正△ABC中,![]() ·
·![]() =
_____________
.
=
_____________
.
16. (理科)已知f ( x )是可导的偶函数,且 ![]() ,则曲线y = f ( x )在(–1,2)处的切线方程是____________
.
,则曲线y = f ( x )在(–1,2)处的切线方程是____________
.
(文科)设P是曲线y = x2 – 1上的动点,O为坐标原点,当![]() 2取得最小值时,点P的坐标为 .
2取得最小值时,点P的坐标为 .
一. 选择题 : 本大题共12小题, 每小题5分, 共60分. ) .
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | 理B文A | B | B | A | D | B | 理D 文B | A | C | C | D | B |
二. 填空题: 本大题有4小题, 每小题4分, 共16分.
13. 960x3 .
15. (理科)![]() 文科)–8
文科)–8
16. (理科)y = 4x + 6. (文科)(–![]() , –
, –![]() )或 (
)或 (![]() ,–
,–![]() ) .
) .
三基小题训练二十三
命题:王统好
一、选择题
1.设集合M =![]() ,
,![]() ,若M∩N
=
,若M∩N
=![]() ,则实数m的取值范围是 ( C )
,则实数m的取值范围是 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.若函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() ( A )
( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若![]() 二项展开式的第5项是常数项,则自然数n的值为 ( C )
二项展开式的第5项是常数项,则自然数n的值为 ( C )
A.6 B.10 C.12 D.15
4.已知等差数列{an}的前n项和为![]() ,若
,若![]() ,则
,则![]() 等于 ( A )
等于 ( A )
A.72 B.54 C.36 D.18
5.给定两个向量![]() ,
,![]() ,若
,若![]() 与
与![]() 平行,则x的值等于( D )
平行,则x的值等于( D )
A.1 B.2 C.![]() D.
D.![]()
6.不等式![]() 的解集为 ( B )
的解集为 ( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.已知函数y = 2sin(ωx)在[![]() ,
,![]() ]上单调递增,则实数ω的取值范围是( A )
]上单调递增,则实数ω的取值范围是( A )
A.(0,![]()
![]() B.(0,2
B.(0,2![]() C.(0,1
C.(0,1![]() D.
D.![]()
8.若直线![]() 与圆
与圆![]() 交于M、N两点,并且M、N关于直线
交于M、N两点,并且M、N关于直线![]() 对称,则不等式组
对称,则不等式组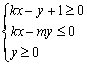 表示的平面区域的面积是 ( A )
表示的平面区域的面积是 ( A )
A.![]() B.
B.![]() C.1 D.2
C.1 D.2
9.椭圆的焦点为F1、F2,过点F1作直线与椭圆相交,被椭圆截得的最短的线段MN长为![]() ,
,![]() 的周长为20,则椭圆的离心率为 ( B )
的周长为20,则椭圆的离心率为 ( B )
A.![]() B.
B.![]() C.
C.![]() (D)
(D)![]()
10.已知二次函数f (x) = x2 + x + a(a>0),若f (m) < 0,则f (m + 1)的值是 ( A )
A.正数 B.负数 C.零 D.符号与a有关
11.已知函数f (x)(0 ≤ x
≤1)的图象的一段圆弧(如图所示)若![]() ,则( C )
,则( C )
 A.
A.![]()
B.![]()
C.![]()
D.前三个判断都不正确
12.点P在直径为![]() 的球面上,过P作两两垂直的3条弦,若其中一条弦长是另一条弦长的2倍,则这3条弦长之和的最大值是 ( D )
的球面上,过P作两两垂直的3条弦,若其中一条弦长是另一条弦长的2倍,则这3条弦长之和的最大值是 ( D )
A. B.6 C.![]() D.
D.![]()
二、填空题
13.(自编)对甲乙两学生的成绩进行抽样分析,各抽取5门功课,得到的观测值如下:
甲:70 80 60 70 90
乙:80 60 70 84 76
那么,两人中各门功课发展较平稳的是 乙 .
解答:![]() ,故
,故![]() .
.
14.(自编)当![]()
![]() 时,
时,![]() 在
在![]() 上是减函数.
上是减函数.
解答:![]() ,由题意知
,由题意知![]() 是函数的单调减区间,因此
是函数的单调减区间,因此![]() .
.
15.(自编)“渐减数”是指每个数字比其左边数字小的正整数(如98765),若把所有五位渐减数按从小到大的顺序排列,则第55个数为 76542 .
解答:4在首位,有1个;5在首位,有![]() 个;6在首位,有
个;6在首位,有![]() 个;7在首位,有
个;7在首位,有![]() 个.所以第55个数是76542.
个.所以第55个数是76542.
16.(2004浙江高三第二次教学质量检测)AB垂直于![]() 所在的平面,
所在的平面,![]() ,当
,当![]() 的面积最大时,点A到直线CD的距离为
的面积最大时,点A到直线CD的距离为![]() .
.
三基小题训练二十四
命题:王统好
一、选择题:(每题5分,共60分)
1.已知a为不等于零的实数,那么集合![]() 的子集的个数为
的子集的个数为
A.1个 B.2个 C.4个 D.1个或2个或4个
2.函数![]() 的最小正周期是
的最小正周期是
A.![]() B.π
C.2π D.3π
B.π
C.2π D.3π
3.已知关于x的不等式![]() 的解集是[-1,0)则a+b=
的解集是[-1,0)则a+b=
A.-2 B.-1 C.1 D.3
4.过双曲线![]() 的右焦点作直线l交双曲线于A、B两点,若
的右焦点作直线l交双曲线于A、B两点,若![]() =4,则满足条件的直线l有
=4,则满足条件的直线l有
A.2条 B.3条 C.4条 D.无数条
5.若向量![]() 的夹角是
的夹角是
A.30° B.60° C.90° D.120°
6.设a、b是两条异面直线,P是a、b外的一点,则下列结论正确的是
A.过P有一条直线和a、b都平行;B.过P有一条直线和a、b都相交;
C.过P有一条直线和a、b都垂直;D.过P有一个平面和a、b都垂直。
7.互不相等的三个正数![]() 成等比数列,且点
成等比数列,且点
P1(![]()
![]() 共线
共线
![]() 则
则![]() ,
,![]()
A.等差数列,但不等比数列; B.等比数列而非等差数列
C.等比数列,也可能成等差数列 D.既不是等比数列,又不是等差数列
8.若从集合P到集合Q=![]() 所有的不同映射共有81个,则从集合Q到集合P可作的不同映射共有
所有的不同映射共有81个,则从集合Q到集合P可作的不同映射共有
A.32个 B.27个 C.81个 D.64个
9.对于函数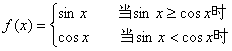 给出下列四个命题:
给出下列四个命题:
①该函数的值域为[-1,1]
②当且仅当![]()
③该函数是以π为最小正周期的周期函数;
④当且仅当![]()
上述命题中错误命题的个数为
A.1 B.2 C.3 D.4
10.已知球的表面积为20π,球面上有A、B、C三点,如果AB=AC=2,BC=2![]() ,则球心到平面ABC的距离为
,则球心到平面ABC的距离为
A.1 B.![]() C.
C.![]() D.2
D.2
11.设x、y满足约束条件: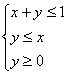 则
则![]() 的最大值为
的最大值为
A.1 B.2 C.3 D.4
12.已知等差数列![]() ,那么,一定有
,那么,一定有
A.![]() C、
C、![]()
二、填空题:(每題4分,共16分)
13.椭圆![]() 中,以点M(一1,2)为中点的弦所在直线方程是___________。
中,以点M(一1,2)为中点的弦所在直线方程是___________。
14.在![]() )
)![]() 的展开式中,x3的系数是_________。
的展开式中,x3的系数是_________。
15.在△ABC中,边AB为最长边,且sinA·sinB=![]() ,则cosA·cosB的最大值是
。
,则cosA·cosB的最大值是
。
16.一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于n2,则算过关,那么,连过前二关的概率是。_______。
一、选择题:(每题5分,共60分)
1.D 2. A 3.C 4.B 5.C 6.C 7.C 8.D 9.D 10.A 11.B 12.B
二、填空题:(每题4分,共16分)
13.![]() 14.
14.![]() 15.
15. ![]() 16.
16.![]()
三基小题训练二十五
命题:王统好
一、填空题(4′×12)
1.函数![]() 图象恒过定点
图象恒过定点![]() ,若
,若![]() 存在反函数
存在反函数![]() ,则
,则![]() 的图象必过定点
的图象必过定点 ![]() 。
。
2.已知集合![]() ,集合
,集合![]() ,则集合
,则集合![]()
![]()
![]() 。
。
3.若角![]() 终边落在射线
终边落在射线![]() 上,则
上,则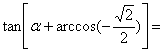
![]() 。
。
4.关于![]() 的方程
的方程![]() 有一实根为
有一实根为![]() ,则
,则![]()
![]() 。
。
5.数列![]() 的首项为
的首项为![]() ,且
,且![]() ,记
,记![]() 为数列
为数列![]() 前
前![]() 项和,则
项和,则![]()
![]()
![]() 。
。
6.新教材同学做:
若![]() 满足
满足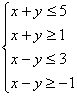 ,则目标函数
,则目标函数![]() 取最大值时
取最大值时![]()
![]() 。
。
老教材同学做:
若![]() 的展开式中第3项为常数项,则展开式中二项式系数最大的是第
的展开式中第3项为常数项,则展开式中二项式系数最大的是第 ![]() 项。
项。
7.已知函数![]() ,若对任意
,若对任意![]() 有
有![]() 成立,则方程
成立,则方程![]() 在
在![]() 上的解为
上的解为 ![]() 。
。
8.新教材同学做:
某校高二(8)班四位同学的数学期中、期末和平时成绩可分别用矩阵
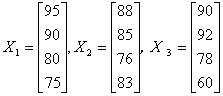 表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵
表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵![]() 可用
可用![]() 表示为
表示为 ![]() 。
。
老教材同学做:
某足球队共有11名主力队员和3名替补队员参加一场足球比赛,其中有2名主力和1名替补队员不慎误服违禁药物,依照比赛规定,比赛后必须随机抽取2名队员的尿样化验,则能查到服用违禁药物的主力队员的概率为 ![]() 。(结果用分数表示)
。(结果用分数表示)
9.将最小正周期为![]() 的函数
的函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到偶函数图象,则满足题意的
个单位,得到偶函数图象,则满足题意的![]() 的一个可能值为
的一个可能值为 ![]() 。
。
10.据某报《自然健康状况》的调查报道,所测血压结果与相应年龄的统计数据如下表,观察表中数据规律,并将最适当的数据填入表中括号内。
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 | …… |
| 收缩压 (水银柱/毫米) | 110 | 115 | 120 | 125 | 130 | 135 | (140) | 145 | …… |
| 舒张压 (水银柱/毫米) | 70 | 73 | 75 | 78 | 80 | 73 | 85 | (88) | …… |
 11.若函数
11.若函数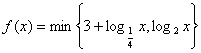 ,其中
,其中![]() 表示
表示![]() 两者中的较小者,
两者中的较小者,
则![]() 的解为
的解为 ![]() 。
。
12.如图,![]() 是一块半径为1的半圆形纸板,在
是一块半径为1的半圆形纸板,在![]() 的左下端剪去一个半径
的左下端剪去一个半径
为![]() 的半圆得到图形
的半圆得到图形![]() ,然后依次剪去一个更小的半圆(其直径是前
,然后依次剪去一个更小的半圆(其直径是前
一个被剪掉半圆的半径)可得图形![]() ,记纸板
,记纸板![]() 的面积为
的面积为![]() ,则
,则![]()
![]() 。
。
二、选择题(4′×4)
13.已知![]() 满足
满足![]() ,则下列选项中不一定能成立的是
( C
)
,则下列选项中不一定能成立的是
( C
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
14.下列命题正确的是 ( C )
A、若![]() ,
,![]() ,则
,则![]() 。
。
B、函数![]() 的反函数为
的反函数为![]() 。
。
C、函数![]() 为奇函数。
为奇函数。
D、函数![]() ,当
,当![]() 时,
时,![]() 恒成立。
恒成立。
15.函数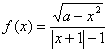 为奇函数的充要条件是
( B
)
为奇函数的充要条件是
( B
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
16.不等式![]() 对任意
对任意![]() 都成立,则
都成立,则![]() 的取值范围为
( B
)
的取值范围为
( B
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
三基小题训练二十六
命题:王统好
一、选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.已知![]() 为三角形的一个内角,且
为三角形的一个内角,且![]() =表示( )
=表示( )
A.焦点在x轴上的椭圆 B.焦在点y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
2.双曲线![]() 两焦点为F1,F2,点P在双曲线上,直线PF1,PF2倾斜角之差为
两焦点为F1,F2,点P在双曲线上,直线PF1,PF2倾斜角之差为![]()
则△PF1F2面积为 ( )
A.16![]() B.32
B.32![]() C.32 D.42
C.32 D.42
3.要使直线![]() 与焦点在x轴上的椭圆
与焦点在x轴上的椭圆![]() 总有公共点,实数a的取
总有公共点,实数a的取
值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.与双曲线![]() 有共同渐近线,且过
有共同渐近线,且过![]() 的双曲线的一个焦点到一条渐近
的双曲线的一个焦点到一条渐近
线的距离是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.过点M(-2,0)的直线m与椭圆![]() 交于P1,P2,线段P1P2的中点为P,设直线m的斜率为k1(
交于P1,P2,线段P1P2的中点为P,设直线m的斜率为k1(![]() ),直线OP的斜率为k2,则k1k2的值为 ( )
),直线OP的斜率为k2,则k1k2的值为 ( )
A.2 B.-2 C.![]() D.-
D.-![]()
6.设![]() 为单元素集,则t值的个数是 ( )
为单元素集,则t值的个数是 ( )
A.1 B.2 C.3 D.4
7.a、b是两条异面直线,下列结论正确的是 ( )
A.过不在a、b上的任一点,可作一个平面与a、b都平行
B.过不在a、b上的任一点,可作一条直线与a、b都相交
C.过不在a、b上的任一点,可作一条直线与a、b都平行
D.过a可以且只可以作一个平面与b平行
8.已知点F1、F2分别是双曲线![]() 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2为锐角三角形,则该双曲线的离心率e的范围是( )
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2为锐角三角形,则该双曲线的离心率e的范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.过抛物线![]() 的焦点F的直线m的倾斜角
的焦点F的直线m的倾斜角![]() 交抛物线于A、B两点,且A点在x轴上方,则FA的取值范围是 ( )
交抛物线于A、B两点,且A点在x轴上方,则FA的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.在正方体ABCD—A1B1C1D1中,O为AC、BD的交点,则C1O与A1D所成的角为( )
A.60° B.90° C.![]() D.
D.![]()
11.直平行六面体ABCD—A1B1C1D1的棱长均为2,![]() ,则对角线A1C与侧面DCC1D1所成角的正弦值为 ( )
,则对角线A1C与侧面DCC1D1所成角的正弦值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.正方体ABCD—A1B1C1D1中,P在侧面BCC1B1及其边界上运动,且总保持AP⊥BD1,则动点P的轨迹是 ( )
A.线段B1C B.线段BC1
C.BB1中点与CC1中点连成的线段 D.BC中点与B1C1中点连成的线段
二、填空题(本大题共4小题,每小题4分,共16分)
13.在棱长为1的正方体ABCD—A1B1C1D1中,O为正方形ABCD的中心,E、F分别为AB、BC的中点,则异面直线C1O与EF的距离为 .
14.已知抛物线![]() 上两点
上两点![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,那么m的值为
.
,那么m的值为
.
15.从双曲线![]() 上任意一点P引实轴平行线交两渐近线于Q、R两点,则PQPR之值为
.
上任意一点P引实轴平行线交两渐近线于Q、R两点,则PQPR之值为
.
16.过抛物线![]() 焦点F的直线与抛物线交于P、Q,由P、Q分别引其准线的垂线PH1、QH2垂足分别为H1、H2,H1H2的中点为M,记PF=a,QF=b,则MF=
焦点F的直线与抛物线交于P、Q,由P、Q分别引其准线的垂线PH1、QH2垂足分别为H1、H2,H1H2的中点为M,记PF=a,QF=b,则MF=
。
一、选择题:(本大题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | A | C | C | D | D | D | B | A | D | D | A |
二、填空题(本大题共12小题,每小题5分,共60分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
三基小题训练二十七
命题:王统好
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合![]() ,则使
,则使![]() 的集合
的集合![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.已知抛物线![]() ,则它的焦点坐标是( )
,则它的焦点坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知向量![]() ,
,![]() ,且
,且![]() ∥
∥![]() ,则
,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.![]() 是
是![]() 所在的平面内的一点,且满足
所在的平面内的一点,且满足![]() ,则
,则![]() 的形状一定为
的形状一定为
A.正三角形 B.等腰直角三角形 C.直角三角形 D.斜三角形
5.为了得到函数![]() 的图象,只须将函数
的图象,只须将函数![]() 的图象
的图象
A.向右平移![]() 个单位
B.向左平移
个单位
B.向左平移![]() 个单位
个单位
C.向右平移![]() 个单位
D.向左平移
个单位
D.向左平移![]() 个单位
个单位
6.若双曲线![]() 两渐近线的夹角为
两渐近线的夹角为![]() ,则
,则![]() 的值为
的值为
A.![]() B.
B.![]() C.4或
C.4或![]() D.2或
D.2或![]()
7.数列![]() 中,
中,![]() ,
,![]() ,且数列
,且数列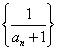 是等差数列,则
是等差数列,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.5
D.5
8.已知![]() ,记数列
,记数列![]() 的前
的前![]() 项和为
项和为![]() ,则使
,则使![]() 的
的![]() 的最小值为
的最小值为
A.10 B.11 C.12 D.13
9.同时掷两颗骰子,则下列命题中正确的是
A.“两颗点数都是5”的概率比“两颗点数都是6”的概率小
B.“两颗点数相同”的概率是![]()
C.“两颗点数之和为奇数”的概率小于“两颗点数之和为偶数”的概率
D.“两颗点数之和为6”的概率不大于“两颗点数之和为5”的概率
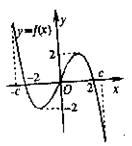 10.
10.![]() 是定义在区间
是定义在区间![]() 上的奇函数,其图象如图所示。令
上的奇函数,其图象如图所示。令![]() ,则下列关于函数
,则下列关于函数![]() 的叙述正确的是
的叙述正确的是
A.若![]() ,则函数
,则函数![]() 的图象关于原点对称
的图象关于原点对称
B.若![]() ,
,![]() ,则方程
,则方程![]() 必有三个实根
必有三个实根
C.若![]() ,
,![]() ,则方程
,则方程![]() 必有两个实根
必有两个实根
D.若![]() ,
,![]() ,则方程
,则方程![]() 必有大于2的实根
必有大于2的实根
11.若记地球的半径为R,则赤道上两地A、B间的球面距离为![]() ,北半球的C地与A、B两地的球面距离均为
,北半球的C地与A、B两地的球面距离均为![]() ,则C地的纬度为
,则C地的纬度为
A.北纬45° B.北纬60° C.北纬30° D.北纬75°
12.设奇函数![]() 在区间
在区间![]() 上是增函数,且
上是增函数,且![]() 。当
。当![]() 时,函数
时,函数![]() ,对一切
,对一切![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围为
的取值范围为
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]() 或
或![]()
二、填空题:本大题共有4个小题,每小题4分,共16分。把答案填在题中横线上。
13.不等式![]() 的解集为_______________。
的解集为_______________。
14.在![]() 的展开式中,含
的展开式中,含![]() 项的系数为____________。
项的系数为____________。
15.如图,在正方体![]() 中,
中,![]() 是正方体的一条面对角线。现有下列命题:
是正方体的一条面对角线。现有下列命题:
 ①过
①过![]() 且与
且与![]() 平行的平面有且只有一个;
平行的平面有且只有一个;
②过![]() 且与
且与![]() 垂直的平面有且只有一个;
垂直的平面有且只有一个;
③![]() 与平面
与平面![]() 所成的角等于30°;
所成的角等于30°;
④与![]() 所成角为60°的面对角线共有8条。
所成角为60°的面对角线共有8条。
上述命题中,正确的是_______________。(填上所有正确命题的序号)
16.密码的使用对现代社会是极其重要的。有一种密码其明文和密文的字母按A、B、C…与26个自然数1,2,3,…依次对应。设明文的字母对应的自然数为![]() ,译为密文的字母对应的自然数为
,译为密文的字母对应的自然数为![]() 。例如,有一种译码方法是按照以下的对应法则实现的:
。例如,有一种译码方法是按照以下的对应法则实现的:
![]() ,其中
,其中![]() 是
是![]() 被26除所得的余数与1之和(
被26除所得的余数与1之和(![]() )。
)。
按照此对应法则,明文A译为了密文F,那么密文UI译成明文为______________。
三基小题训练二十八
命题:王统好
一、选择题:本大题共8个小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设全集U = R ,A =![]() ,则
,则![]() UA=
( )
UA=
( )
(A)![]() (B){x x > 0} (C){x x≥0} (D)
(B){x x > 0} (C){x x≥0} (D)![]() ≥0
≥0![]()
(2)在等差数列{![]() }中,
}中,![]() =-5,
=-5,![]() ,则
,则![]() 等于
( )
等于
( )
(A)-4 (B)-5 (C)-7 (D)-8
(3)函数y =
![]() (x≠-1)的反函数是
( )
(x≠-1)的反函数是
( )
(A)y =![]() –1 (x≠0)
(B)y=
–1 (x≠0)
(B)y=![]() +1 (x≠0)
+1 (x≠0)
(C)y = –x + 1 (x∈R) (D)y= – x–1 (x∈R)
(4)若![]() ,
,![]() 且(
且(![]() )⊥
)⊥![]() ,则
,则![]() 与
与![]() 的夹角是 ( )
的夹角是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(5)已知m、n为两条不同的直线,![]() 、
、![]() ,为 两个不同的平面,m⊥
,为 两个不同的平面,m⊥![]() ,n⊥
,n⊥![]() ,则下列命题中的假命题是
( )
,则下列命题中的假命题是
( )
(A)若![]() ∥n ,则
∥n ,则![]() ∥
∥![]() (B)若
(B)若![]() ⊥
⊥![]() ,则m⊥n
,则m⊥n
(C)若![]() 、
、![]() 相交,则m 、n相交
(D)若m、n相交,则
相交,则m 、n相交
(D)若m、n相交,则![]() 、
、![]() 相交
相交
(6)箱子里有5 个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(7)如果三位数的十位数字既大于百位数字也大于个位数字,则这样的三位数一共有( )
(A)240个 (B)285个 (C)231个 (D)243个
(8)以正方形ABCD的相对顶点A、C为焦点的椭圆,恰好过正方形四边的中点,则该椭圆的离心率为 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。
(9)把y =
sinx的图象向左平移![]() 个单位,得到函数________________________的图象;再把所得图象上的所有点的横坐标伸长到原来的2倍,而纵坐标保持不变,得到函数_____________________的图象。
个单位,得到函数________________________的图象;再把所得图象上的所有点的横坐标伸长到原来的2倍,而纵坐标保持不变,得到函数_____________________的图象。
(10)已知直线![]() :x – 2y + 3 = 0 ,那么直线
:x – 2y + 3 = 0 ,那么直线![]() 的方向向量
的方向向量![]() 为_______________(注:只需写出一个正确答案即可);
为_______________(注:只需写出一个正确答案即可);![]() 过点(1,1),并且
过点(1,1),并且![]() 的方向向量
的方向向量![]() 2与
2与![]() 1满足
1满足![]() 1·
1·![]() = 0,则
= 0,则![]() 的方程为___________________________________________。
的方程为___________________________________________。![]()
|
|
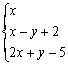 ≤0 ,则z = x + y的最大值是____________________.
≤0 ,则z = x + y的最大值是____________________.
(12)若地球半径为R,地面上两点A、B的纬度均为北纬45°,又A、B两点的球面距离为![]() ,则A、B两点的经度差为___________________。
,则A、B两点的经度差为___________________。
|
|
(14)某网络公司,1996年的市场占有率为A,根据市场分析和预测,该公司自1996年起市场占有率逐年增加,其规律如图所示:
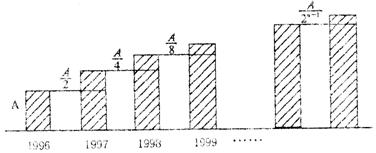
则该公司1998年的市场占有率为____________;如果把1996年作为第一年,那么第n年的市场占有率为________________________________
一、选择题
(1)C (2)D (3)A (4)B (5)C (6)B (7)A (8)D
二、填空题
(9)y =
sin![]() ,
,![]() ; (10)(2,1)或
; (10)(2,1)或![]() 等,2x + y – 3 = 0;
等,2x + y – 3 = 0;
(11)5; (12)90°; (13)![]() ; (14)
; (14)![]() .
.
注:(9)、(10)、(14)小题第一个空2分,第二个空3分.
三基小题训练二十九
命题:王统好
一、填空题(每题5分,共50分,请正确答案填在横线上)
1.
已知![]() ,若
,若 ![]() ,则k 的值是___________.
,则k 的值是___________.
2. 在![]() 的展开式中,
的展开式中,![]() 的系数是_____。
的系数是_____。
3.抛物线y2=8x上一点M到焦点的距离为5,则点M到y轴的距离为__________
4.若![]() ,则x的取值范围是____________.
,则x的取值范围是____________.
5.复数![]() 的共轭复数是____________。
的共轭复数是____________。
6.在![]() 中,三边之比为
中,三边之比为![]() ,则
,则![]() 最大角的大小是_________。
最大角的大小是_________。
7.若函数f(x)的图象与g(x)=2x-1的图象关于直线y=x对称,则函数f(x)的解析式为f(x)=_____。
8. A点关于8x+6y=25的对称点恰为原点,则A点的坐标为___________
9.已知![]() 且x+y=4,求
且x+y=4,求![]() 的最小值。某学生给出如下解法:由x+y=4得,
的最小值。某学生给出如下解法:由x+y=4得,![]() ①,即
①,即![]() ②,又因为
②,又因为![]() ③,由②③得
③,由②③得![]() ④,即所求最小值为
④,即所求最小值为![]() ⑤。请指出这位同学错误的原因 ___________________________。
⑤。请指出这位同学错误的原因 ___________________________。
10、若定义在区间[3-a,5]上的函数![]() 是奇函数,则a+b=_______.
是奇函数,则a+b=_______.
二、选择题(每小题5分,每小题只有一个正确答案)
11、设a,b是两条不重合的直线,![]() 是三个不重合的平面, 那么
是三个不重合的平面, 那么![]() 的一个充分条件是( )
的一个充分条件是( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
12.直线(x+1)a+(y+1)b=0与圆x2+y2=2的位置关系是……( )
A.相交 B.相离 C.相切或相离 D.相切或相交
13. 已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于 ( )
(A)-4 (B)-6 (C)-8 (D)-10
14.已知函数f (x)(0≤x≤1) 的图象的一段圆弧(如图所示)若
的图象的一段圆弧(如图所示)若
![]() ,则 ( )
,则 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)前三个判断都不正确
(D)前三个判断都不正确
一、
1、6 2、40 3、3 4、![]() 5、1-2i 6、120。 7、y=
5、1-2i 6、120。 7、y=![]()
8、(4,3) 9、①③两式的等号不能同时成立。 10、8
二、
| 题号 | 11 | 12 | 13 | 14 |
| 答案 | A | D | B | C |
三基小题训练三十
命题:王统好
一、选择题(本题共12小题,每题5分,共60分)
1.已知集合![]() ,Z为整数集,则
,Z为整数集,则![]() 为............ ( )
为............ ( )
A.{2,1}
B.{2,1,0} C.![]() D.{0,-1}
D.{0,-1}
2.已知复数![]() ,则z2对应的点中第( )象限
,则z2对应的点中第( )象限
A.Ⅰ B.Ⅱ C.Ⅲ D.Ⅳ
3.![]() .......................................................... ( )
.......................................................... ( )
A.![]() B.
B.![]() C.1
D.0
C.1
D.0
4.函数![]() 是R上的偶函数,则
是R上的偶函数,则![]() 的值是 ( )
的值是 ( )
A.0
B.![]() C.
C.![]() D.
D.![]()
5.由圆![]() 与区域
与区域![]() 所围图形(含边界)含整点(纵横坐标都为整数的点)的个数为 ( )
所围图形(含边界)含整点(纵横坐标都为整数的点)的个数为 ( )
A.2 B.3 C.4 D.5
6.数列![]() 中,若对
中,若对![]() ,有
,有![]() ,且,
,且,![]() 则
则![]() ( )
( )
A.2 B.-2 C.±2 D.0
7.![]() 为非零向量,
为非零向量,![]() ,则
,则![]() 与
与![]() 的夹角为.... ( )
的夹角为.... ( )
A.300 B.450 C.600 D.900
8.函数![]() 相邻两条对称轴的距离为........ ( )
相邻两条对称轴的距离为........ ( )
A.2![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.过曲线![]() 上点P处的切线平行于直线
上点P处的切线平行于直线![]() ,则点P的坐标为()
,则点P的坐标为()
A.(0,1) B.(-1,0) C.(1,3) D.(-1,3)
10.地球仪上北纬300纬线圈周长为12![]() cm,则地球仪的表面积为( )
cm,则地球仪的表面积为( )
A.48![]() cm2
B.2304
cm2
B.2304![]() cm2
C.576
cm2
C.576![]() cm2
D.192
cm2
D.192![]() cm2
cm2
11.若![]() 且
且![]() ,则实数m的值为 ( )
,则实数m的值为 ( )
A.1 B.-1 C.-3 D.1或-3
12.一个正方体,它的表面涂满了红色,把它切割成27个完全相等的小正方体,从中任取2个,其中1个恰有一面涂有红色,另1个恰有两面涂有红色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本题共4小题,每题4分,共14分)
13.若双曲线![]() 过点
过点![]() ,则该双曲线的焦距为______
,则该双曲线的焦距为______
14.若![]() 则
则![]() __________
__________
15.已知![]() 是定义在(-∞,+∞)上的减函数,其图像经过A(-4,1),B(0,-1)两点,
是定义在(-∞,+∞)上的减函数,其图像经过A(-4,1),B(0,-1)两点,![]() 的反函数是
的反函数是![]() ,则
,则![]() _____;不等式
_____;不等式![]() 的解集是____
的解集是____
16.给出下列四个命题:①各侧面都是正方形的棱柱一定是正棱柱;②若一个简单多面体的各顶点都有3条棱,则其顶点数V、面数F满足的关系式为2F-V=4;③若直线λ⊥平面α,λ//平面β,则α⊥β;④命题“异面直线a、b不垂直,则过a的任一平面与b都不垂直”的否定。其中,正确的命题是_____________
参考答案
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| B | A | A | C | C | B | A | C | A | D | D | C |
13.![]() 14.0 15.-4
14.0 15.-4 ![]() 16.②③
16.②③
三基小题训练三十一
命题:王统好
一.选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求的)
1.满足![]() 的集合
的集合![]() 的组数有( )
的组数有( )
(A)4组 (B)6组 (C)7组 (D)9组
2.已知函数![]() ,则其反函数为( )
,则其反函数为( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
3.函数![]() 的图象的一个对称中心为( )
的图象的一个对称中心为( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D)![]()
4.若关于![]() 的不等式
的不等式![]() ≥
≥![]() 在
在![]() 上恒成立,则
上恒成立,则![]() 的最大值为( )
的最大值为( )
(A)![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
5.给定性质:①最小正周期为![]() ②图象关于直线
②图象关于直线![]() 对称,则下列函数中同时具有性质①、②的是( )
对称,则下列函数中同时具有性质①、②的是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
6.已知△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]() 或
或![]()
7.(理)等差数列![]() 中,
中,![]() 且
且![]() ,则
,则![]() 项是( )
项是( )
(A)一个正数 (B)一个负数 (C)零 (D)符号不能确定.
(文)等比数列![]() 中,
中,![]() ,则
,则![]() (
)
(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
8.偶函数![]() 在
在![]() 单调递减,若
单调递减,若![]() 是锐角三角形的两个内角,则( )
是锐角三角形的两个内角,则( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
9.设![]() 表示不超过
表示不超过![]() 的最大整数(例[5.5]=5,[-5.5]=-6),则不等式
的最大整数(例[5.5]=5,[-5.5]=-6),则不等式![]() ≤
≤![]() 的解集为( )
的解集为( )
(A)(2,3) (B)[2,4) (C)[2,3] (D)[2,4]
10.(理)![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(文)等差数列![]() 中,若
中,若![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11.正四面体![]() 中,
中,![]() 分别为棱
分别为棱![]() 和
和![]() 上的点,且
上的点,且![]() ,设
,设![]() (其中
(其中
![]() 表示
表示![]() 与
与![]() 成的角,
成的角,![]() 表示
表示![]() 与
与![]() 成的角),则( )
成的角),则( )
(A) ![]() 在
在![]() 单调递增 (B)
单调递增 (B) ![]() 在
在![]() 单调递减
单调递减
(C) ![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减 (D)
单调递减 (D) ![]() 在
在![]() 为常函数
为常函数
12.数列![]() 的前
的前![]() 项和
项和![]() 与通项
与通项![]() 满足关系式
满足关系式![]() ,则
,则![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
二.填空题:(本大题共4小题,每小题4分,共16分)
13.若实数![]() 满足
满足![]() 且
且![]() ≤0,则
≤0,则![]() 的最小值为 .
的最小值为 .
14.若![]() 是以5为周期的奇函数,且
是以5为周期的奇函数,且![]() ,则
,则![]() .
.
15.若关于![]() 的不等式
的不等式![]() 的解集为(0,2),则实数
的解集为(0,2),则实数![]() 的值为 .
的值为 .
16.以下5个命题:
①对实数![]() 和向量
和向量![]() 与
与![]() ,恒有
,恒有![]()
②对实数![]() 和向量
和向量![]() ,恒有
,恒有![]()
③若![]() ,则
,则![]()
④若![]() ,则
,则![]()
⑤对任意的向量![]() ,恒有
,恒有![]()
写出所有真命题的序号 .
一.选择题:1.D;2.B;3.B;4.B;5.D;6.C;7.(理)B;(文)C;8.A;9.B;10. (理)B; (文)A;11.D;12.C.
二.填空题: 13.![]() ;14.
;14.![]() ;15.1;16.①②⑤
;15.1;16.①②⑤
三基小题训练三十二
命题:王统好
一、选择题(5¢×12=60¢)
1. 函数y=3sinx+4cosx+5的最小正周期是
A.![]() B.
B.![]() C.p D.2p
C.p D.2p
2.
已知定义域在[-1,1]上的函数y=f(x)的值域为[-2,0],则函数y=f(cos![]() )的值域为
)的值域为
A.[-1,1] B.[―3,―1] C.[-2,0] D.不能确定
3. 已知函数y=f(x)是一个以4为最小正周期的奇函数,则f(2)=
A.0 B.-4 C.4 D.不能确定
4.
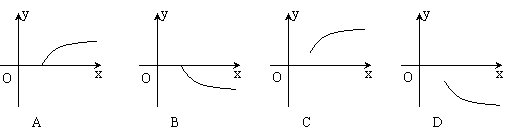 设f(x-1)=x2-2x+3 (x≤1),则函数
设f(x-1)=x2-2x+3 (x≤1),则函数![]() 的图象为
的图象为
5. 首项系数为1的二次函数y=f(x)在x=1处的切线与x轴平行,则
A.f(arcsin![]() )>f(arcsin
)>f(arcsin![]() ) B.f(arcsin
) B.f(arcsin![]() )=f(arcsin
)=f(arcsin![]() )
)
C.f(arcsin![]() )>f(arcsin
)>f(arcsin![]() ) D.f(arcsin
) D.f(arcsin![]() )与f(arcsin
)与f(arcsin![]() )的大小不能确定
)的大小不能确定
6.
关于x的不等式ax-b>0的解集为(1,+∞),则关于x的不等式![]() >0的解集为
>0的解集为
A.(-1,2) B.(-∞,-1)∪(2,+∞) C.(1,2) D.(―∞,―2)∪(1,+∞)
7.
若O为⊿ABC的内心,且满足(![]() -
-![]() )•(
)•(![]() +
+![]() -2
-2![]() )=0
)=0
A.等腰三角形 B.正三角形 C.直角三角形 D.以上都不对
8. 设有如下三个命题
甲:m∩l=A, m、l![]() a, m、l
a, m、l![]() b;
b;
乙:直线m、l中至少有一条与平面b相交;
丙:平面a与平面b相交。
当甲成立时,乙是丙的 条件。
A.充分而不必要 B.必要而不充分 C.充分必要 D.既不充分又不必要
9. ⊿ABC中,3sinA+4cosB=6,3cosA+4sinB=1,则∠C的大小为
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
10. 等体积的球和正方体,它们的表面积的大小关系是
A.S球>S正方体 B.S球<S正方体 C.S球=S正方体 D.S球=2S正方体
11. 若连结双曲线![]() -
-![]() =1与其共轭双曲线的四个顶点构成面积为S1的四边形,连结四个焦点构成面积为S2的四边形,则
=1与其共轭双曲线的四个顶点构成面积为S1的四边形,连结四个焦点构成面积为S2的四边形,则![]() 的最大值为
的最大值为
A.4 B.2 C.![]() D.
D.![]()
12. 若干个正方体形状的积木按如图所示摆成塔形,上面正方体中下底的四个顶点是下面相邻正方体中上底各边的中点,最下面的正方体的棱长为1,平放在桌面上,如果所有正方体能直接看到的表面积超过7,则正方体的个数至少是
A.2 B.3 C.4 D.6
二、填空题(4¢×4=16¢)
13. 若指数函数f(x)=ax (x∈R)的部分对应值如下表:
| x | -2 | 0 | 2 |
| f(x) | 0.694 | 1 | 1.44 |
则不等式![]() (x-1)<0的解集为 。
(x-1)<0的解集为 。
14. 若两个向量![]() 与
与![]() 的夹角为q,则称向量“
的夹角为q,则称向量“![]() ×
×![]() ”为“向量积”,其长度
”为“向量积”,其长度![]() ×
×![]() =
=![]() •
•![]() •sinq。今已知
•sinq。今已知![]() =1,
=1,![]() =5,
=5,![]() •
•![]() =-4,则
=-4,则![]() ×
×![]() = 。
= 。
15. 已知点P(2,-3),Q(3,2),直线ax+y+2=0与线段PQ相交,则实数a的取值范围是: 。
16. 若在所给的条件下,数列{an}的每一项的值都能唯一确定,则称该数列是“确定的”,在下列条件下,有哪些数列是“确定的”?请把对应的序号填在横线上 。
①{an}是等差数列,S1=a,S2=b(这里的Sn是{an}的前n项的和,a,b为实数,下同);
②{an}是等差数列,S1=a,S10=b;
③{an}是等比数列,S1=a,S2=b;
④{an}是等比数列,S1=a,S3=b;
⑤{an}满足a2n+2=a2n+a,a2n+1=a2n-1+b, (n∈N*), a1=c
一、DCABA BACAB CB
二、13.(0,1)∪(1,2) 14.315.[-![]() ,
,![]() ]16.①②③
]16.①②③
三基小题训练三十三
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项
中,只有一项是符合题目要求的)
1、![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、函数![]() 的最小正周期是( )
的最小正周期是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、首项系数为1的二次函数![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行,则( )
轴平行,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知定义在![]() 上的函数
上的函数![]() 的值域为
的值域为![]() ,则函数
,则函数![]() 的值域为( )
的值域为( )
A.![]() B.
B.![]() C.
C.![]() D.无法确定
D.无法确定
5、函数![]() 的部分图像大致是( )
的部分图像大致是( )
A. B. C. D.
6、关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则关于
,则关于![]() 的不等式
的不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]()
C.(1,2) D.![]()
7、若O为![]() 的内心,且满足
的内心,且满足![]() ,则
,则![]() 的形状为( )
的形状为( )
A.等腰三角形 B.正三角形 C.直角三角形 D.以上都不对
8、若平面![]() 与平面
与平面![]() 相交,直线
相交,直线![]() ,则( )
,则( )
A.![]() 内必存在直线与
内必存在直线与![]() 平行,且存在直线与
平行,且存在直线与![]() 垂直。
垂直。
B.![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,不一定存在直线与
平行,不一定存在直线与![]() 垂直。
垂直。
C.![]() 内不一定存在直线与
内不一定存在直线与![]() 平行,但必存在直线与
平行,但必存在直线与![]() 垂直。
垂直。
D.![]() 内必存在直线与
内必存在直线与![]() 平行,不一定存在直线与
平行,不一定存在直线与![]() 垂直。
垂直。
9、已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,则其各项和S( )
,则其各项和S( )
A.1 B.![]() C.
C.![]() D.
D.![]()
10、当圆锥的侧面积与底面积的比值是![]() 时,圆锥的轴截面的顶角是( )
时,圆锥的轴截面的顶角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、P是双曲线![]() 右支上一点,
右支上一点,![]() 分别是其左、右焦点,且焦距为
分别是其左、右焦点,且焦距为![]() ,则
,则![]() 的内切圆圆心的横坐标为:
的内切圆圆心的横坐标为:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、如图所示,在正方体![]() 的侧面
的侧面![]() 内有一动点P到直线AB与直线
内有一动点P到直线AB与直线![]() 的距离相等,则动点P所在曲线的形状为( )
的距离相等,则动点P所在曲线的形状为( )
A. B. C. D.
二、填空题(本大题4个小题,每小题4分,共16分,只填结果,不要过程)
13、若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
|
| -2 | 0 | 2 |
|
| 0.69 | 1 | 1.44 |
则不等式![]() 的解集为
。
的解集为
。
14、![]() ,且
,且![]() ,则向量
,则向量![]() 。
。
15、已知点![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() 相交,则实数
相交,则实数![]() 的取值范围是
。
的取值范围是
。
16、若在所给条件下,数列![]() 的每一项的值都能唯一确定,则称该数列是“确定的”,在下列各组条件下,有哪些数列是“确定的”?请把对应的序号填在横线上 。
的每一项的值都能唯一确定,则称该数列是“确定的”,在下列各组条件下,有哪些数列是“确定的”?请把对应的序号填在横线上 。
①![]() 是等差数列,
是等差数列,![]() (这里
(这里![]() 是
是![]() 的前
的前![]() 项和,
项和,![]() 为实常数,下同)
为实常数,下同)
②![]() 是等差数列,
是等差数列,![]()
③![]() 是等比数列,
是等比数列,![]()
④![]() 是等比数列,
是等比数列,![]()
⑤![]() 满足
满足![]()
答 案
1.B 2.D 3.C 4.C 5.C 6.B
7.A 8.C 9.A 10.C 11.A 12.C
13.![]() 14.
14.![]() 15.[
15.[![]() ]
] ![]() 16.①②③
16.①②③
三基小题训练三十四
命题:王统好
一、选择题:本大题共12小题,每小题5分。共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
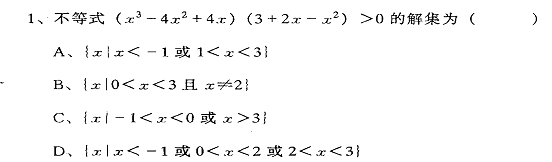

5、从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又
有女生,则不同的选法共有( )
A、140种 B、120种 C、35种 D、34种


8、设 f 1(x)是函数f(x)的导数,y=f 1(x)的图象如图甲所示,则y=f(x)的图象最
有可能是图( )中的图象:
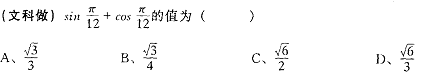 |
10、已知集合M ={直线的倾斜角},集合N ={两条异面直线所成的角},集合P
={直线与平面所成的角},则下列结论中正确的个数为( )
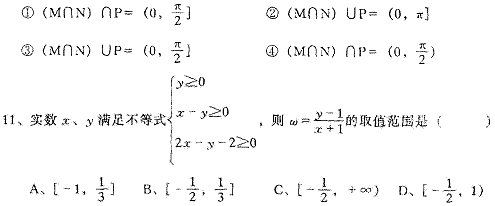 |
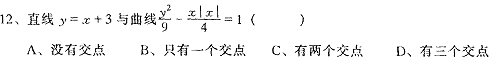
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.
![]()
14、设地球O的半径为R,P和Q是地球上两地,P在北纬45o,东经20o,Q在北
纬45o,东经110o,则P与Q 两地的球面距离为 。
15、(理科做)某同学在一次知识竞赛中有两道必答题,每道题答对得10分,答错扣
5分,假设每题回答正确的概率均为0.7,且各题之间没有影响,则这名同学回答这两道
题的总得分ξ的数学期望是 .
(文科做)若二次函数f(x)满足f(x+1)-f(x)=2x,f(0)=1,则f(x)=
16、下列命题:
(1)在空间,若四点不共面,则每三点一定不共线;
(2)若A(m,10),B(m+2,l0),点P满足PA-PB=1,则点P的轨迹
是双曲线;
(3)一个简单多面体的各面都是三角形,若它的顶点数为V,面数为F,则F与V
问的关系是F=2V-4;
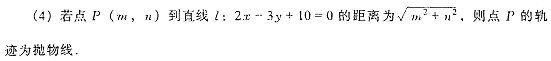
其中正确的命题为
三、解答题:本大题共6小题。共74分,魑答应写出文字说明、证明过程或演变步
其中正确的命题为 。
一、1.D 2.A 3.A 4.D 5.D 6.B
7.C 8.B 9.C 10.C 11. D 12.D
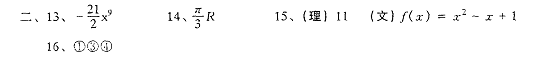
三基小题训练三十五
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的4个选项中,只有1
项是符合题要求的)
1.设![]() ,则满足
,则满足![]() 的集合A,B的组数是 ( )
的集合A,B的组数是 ( )
A.1组 B.2组 C.4组 D.6组
2.若![]() ,则下列各式中成立的是 ( )
,则下列各式中成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.在![]() 中,如果
中,如果![]() ,则角A等于 ( )
,则角A等于 ( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
4.已知数列![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.1 D.-2
C.1 D.-2
5.直线![]() 有交点,但直线不过圆心,则
有交点,但直线不过圆心,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
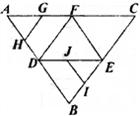 6.如图,在正三角形
6.如图,在正三角形![]() 中,D、E、F分别为各边的中点,G、
中,D、E、F分别为各边的中点,G、
H、I、J分别为AF,AD,BE,DE的中点,将![]() 沿DE,
沿DE,
EF,DF折成三棱锥以后,GH与IJ所成角的度数为 ( )
A.90° B.60°
C.45° D.0°
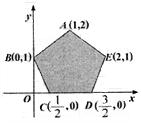 7.已知以
7.已知以![]() 为自变量的目标函数
为自变量的目标函数![]() 的可行域
的可行域
如图阴影部分(含边界),若使![]() 取最大值时的最优解有无穷
取最大值时的最优解有无穷
多个,则k的值为 ( )
A.1 B.![]()
C.2 D.4
8.若![]() ,则函数
,则函数![]() 的最小值是( )
的最小值是( )
A.1 B.-1 C.![]() D.-2
D.-2
9.一个正四面体外切于球O1,同时又内接于球O2,则球O1与球O2的体积之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若把英语单词“hello”的字母顺序写错了,则可能出现的错误的种数是 ( )
A.119 B.59 C.120 D.60
11.E,F是随圆![]() 的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF
的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF
的最大值是 ( )
A.15° B.30° C.60° D.45°
12.关于甲、乙、丙三人参加高考的结果有下列三个正确的判断:①若甲未被录取,则乙、
丙都被录取;②乙与丙中必有一个未被录取;③或者甲未被录取,或者乙被录取,则三
人中被录取的是 ( )
A.甲 B.丙 C.甲与丙 D.甲与乙
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上.)
13.把函数![]() 的图象按向量a平移后,得
的图象按向量a平移后,得![]() 的图象,则a= .
的图象,则a= .
14.已知关于x的不等式![]() 的解集为M,若
的解集为M,若![]() ,则实数a的取值范
,则实数a的取值范
围是 .
15.设![]() 的反函数的解析式是
的反函数的解析式是![]()
.
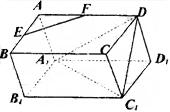 16.若E,F分别是四棱柱ABCD—A1B1C1D1的棱AB,AD
16.若E,F分别是四棱柱ABCD—A1B1C1D1的棱AB,AD
的中点,则加上条件 ,
就可得结论:EF⊥平面DA1C1. (写出你认为正确的一个
条件即可)
1.D 2.C 3.A 4.C 5.B 6.B 7.A 8.A 9.D 10.B 11.B 12.D
13.(-1,-3) 14.![]() 15.
15.![]()
16.底面是菱形且DC1⊥底面(或填AB=BC,AD=CD,DA⊥底面;或填底面是正方形,
DA1⊥A1B1,DA1⊥A1D1等等)
三基小题训练三十六
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有1
项是符合题要求的)
1.若集合![]() 的值是( )
的值是( )
A.-1 B.0或1 C.2 D.0
2.若![]() ,则下列各式中成立的是 ( )
,则下列各式中成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.在![]() 中,如果
中,如果![]() ,则角A等于 ( )
,则角A等于 ( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]()
4.在等差数列![]() 中,若
中,若![]() 的值为 ( )
的值为 ( )
A.20 B.30 C.40 D.50
5.直线![]() 有交点,但直线不过圆心,则
有交点,但直线不过圆心,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
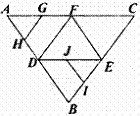 6.如图,在正三角形
6.如图,在正三角形![]() 中,D、E、F分别为各边的中点,G、
中,D、E、F分别为各边的中点,G、
H、I、J分别为AF,AD,BE,DE的中点,将![]() 沿DE,
沿DE,
EF,DF折成三棱锥以后,GH与IJ所成角的度数为 ( )
A.90° B.60°
C.45° D.0°
7.不等式组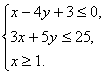 所表示的平面区域图形是 ( )
所表示的平面区域图形是 ( )
A.第一象限内的三角形 B.四边形
C.第三象限内的三角形 D.以上都不对
8.若![]() ,则函数
,则函数![]() 的最小值是( )
的最小值是( )
A.1 B.-1 C.![]() D.-2
D.-2
9.一个正四面体外切于球O1,同时又内接于球O2,则球O1与球O2的体积之比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若把英语单词“hello”的字母顺序写错了,则可能出现的错误的种数是 ( )
A.119 B.59 C.120 D.60
11.E,F是随圆![]() 的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF
的左、右焦点,l是椭圆的一条准线,点P在l上,则∠EPF
的最大值是 ( )
A.15° B.30° C.60° D.45°
12.关于甲、乙、丙三人参加高考的结果有下列三个正确的判断:①若甲未被录取,则乙、
丙都被录取;②乙与丙中必有一个未被录取;③或者甲未被录取,或者乙被录取,则三
人中被录取的是 ( )
A.甲 B.丙 C.甲与丙 D.甲与乙
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上.)
13.把函数![]() 的图象按向量a平移后,得
的图象按向量a平移后,得![]() 的图象,则a= .
的图象,则a= .
14.已知关于x的不等式![]() 的解集为M,若
的解集为M,若![]() ,则实数a的取值范
,则实数a的取值范
围是 .
15.设![]() 的反函数的解析式是
的反函数的解析式是![]()
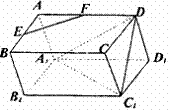 .
.
16.若E,F分别是四棱柱ABCD—A1B1C1D1的棱AB,AD
的中点,则加上条件 ,
就可得结论:EF⊥平面DA1C1. (写出你认为正确的一个
1.D 2.C 3.A 4.C 5.B 6.B 7.A 8.A 9.D 10.B 11.B 12.D
13.(-1,-1) 14.![]() 15.
15.![]()
16.底面是菱形且DC1⊥底面(或填AB=BC,AD=CD,DA⊥底面;或填底面是正方形,
DA1⊥A1B1,DA1⊥A1D1等等)
三基小题训练三十七
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有1项
是符合题目要求的.)
1.给出两个命题:p:x=x的充要条件是x为正实数;q:存在反函数的函数一定是单调函数,则下列哪个复合例题是真命题 ( )
A.p且q B.p或q C.¬p且q D.¬p或q
2.设集合M={xx2-x<0,x∈R},N={xx<2,x∈R},则 ( )
A.M∪N=M B.M∩N=M C.(CRM)∩N=Ø D.(CRN)∩N=R
3.设双曲线 实轴长、虚轴长、焦距成等比数列,则双曲线的离心率为( )
![]()
![]() A.
B.
C.
D.
A.
B.
C.
D.
4.设 则a,b,c的大小关系 ( )
A.a<c<b B.b<c<a C.a<b<c D.b<a<c
5.设有四个命题:①底面是矩形的平行六面体是长方体 ②棱长都相等的直四棱柱是正方体 ③侧棱垂直于底面两条边的平行六面体是直平行六面体 ④对角线相等的平行六面体是直平行六面体,其中真命题的个数是 ( )
A.1 B.2 C.3 D.4
6.数列{an}中,a1=1, ( )
A.0 B.1 C. D.不存在
7.已知f(x)是定义在R上的奇函数,且当x<0时,f(x)=2x,则 的值为 ( )
![]()
![]() A.
B.
C.-2
D.2
A.
B.
C.-2
D.2
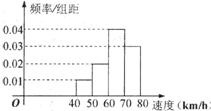 8.如图是150辆汽车通过某路段时速度的频率分布直方图,
8.如图是150辆汽车通过某路段时速度的频率分布直方图,
![]() 则速度在
的汽车大约有( )
则速度在
的汽车大约有( )
A.100辆 B.80辆
C.60辆 D.45辆
![]() 9.设抛物线y2=2px(p>0)的准线为l,将圆x2+y2=9按向量
9.设抛物线y2=2px(p>0)的准线为l,将圆x2+y2=9按向量
=(2,1)平移后恰与l相切,则p的值为 ( )
![]()
![]() A.
B.2
C.
D.4
A.
B.2
C.
D.4
10.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2,值域为{1,4}的“同族函数”共有 ( )
A.9个 B.8个 C.5个 D.4个
11.球面上有三点,其中任意两点的球面距离都等于球的大圆周长的 经过这三点的小圆的周长为4π,则这个球的表面积为 ( )
A.64π B.48π C.24π D.12π
12.要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板块数如下表:
|
| A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
今需A、B、C三种规格的成品各15、18、27块,所需两种规格的钢板的张数分别为m、n(m、n为整数),则m+n的最小值为 ( )
A.10 B.11 C.12 D.13
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
![]() 二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上。)
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上。)
![]() 13.设复数Z满足
.
13.设复数Z满足
.
14.已知: 垂直,则λ= .
15.已知(1-2x)n的展开式中,二项式系数的和为64,则它的二项展开式中,系数最大的是第 项.
![]() 16.在钝角ΔABC中,角A、B、C的对边分别为a、b、c,且a=1,A=30°,c= 则ΔABC的面积为
.
16.在钝角ΔABC中,角A、B、C的对边分别为a、b、c,且a=1,A=30°,c= 则ΔABC的面积为
.
答案:1.D 2.B 3.B 4.A 5.A 6.C 7.D 8.C 9.B 10.A 11.B 12.C
![]() 13.5 14. 15.5 16.
13.5 14. 15.5 16.
三基小题训练三十八
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有1项
是符合题目要求的.)
1.已知集合A={xx2-11x-12<0},集合B={xx=2(3n+1),nZ},则A∩B等于 ( )
A.{2} B.{2,8} C.{4,10} D.{2,4,8,10}
2.如果命题p或q为假命题,则 ( )
A.p、q均为真命题 B.p、q中至少有一个为真命题
C.p、q中至多有一个为真命题 D.p、q均为假命题
3.在100,101,102,…,999这些数中,各位数字按严格递增(如“145”)或严格递减(如“321”)顺序排列的数的个数是 ( )
A.120 B.168 C.204 D.216
4.不等式x+log2x<x+log2x的解集为 ( )
A.(0,1) B.(1,+∞) C.(0,+∞) D.(-∞,+∞)
5.已知α、β以及α+β均为锐角,x=sin(α+β),y=sinα+sinβ,z=cosα+cosβ,那么x、y、z的大小关系是 ( )
A.x<y<z B.y<x<z C.x<z<y D.y<z<x
6.过曲线xy=a2(a≠0)上任意一点处的切线与两坐标轴构成的三角形的面积是 ( )
![]() A.a2
B.
C.2 a2
D.不确定
A.a2
B.
C.2 a2
D.不确定
![]() 7.若 展开式的第3项为144,则
的值是
( )
7.若 展开式的第3项为144,则
的值是
( )
A.2 B.1 C. D.0
8.正四面体的内切球和外接球的半径分别为r和R,则r:R为 ( )
A.1:2 B.1:3 C.1:4 D.1:9
9.已知椭圆的中心在原点,离心率 且它的一个焦点与抛物线y2=4x的焦点重合,则此椭圆的方程为 ( )
A. B.
C. D.
10.如果直线y=kx+1与圆x2+y2+kx+my-4=0交于M、N两点,且M、N关于直线x+y=0对称,
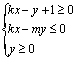 |
则不等式组: 表示的平面区域的面积是 ( )
A. B. C.1 D.2
11.有一条生产流水线,由于改进了设备,预计第一年产量的增长率为150%,以后每年的增长率是前一年的一半,同时,由于设备不断老化,每年将损失年产量的10%,则年产量最高的是改进设备后的 ( )
A.第一年 B.第三年 C.第四年 D.第五年
12.设ΔABC的三边a、b、c满足 an+bn=cn(n>2),则ΔABC是 ( )
A.钝角三角形 B.锐角三角形 C.等腰直角三角形 D.非等腰的直角三角形
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上。)
13.一个容量为n的样本,分成若干组,已知某数的频数和频率分别为36和0.25,则n等于 .
14.设数列{an}的前n项和为Sn, 且a4=54,则a1= .
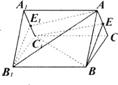 |
15. 如图,已知ABC—A1B1C1是各棱长均为5的正三棱柱,E、E1分别是
AC,A1C1的中点,则平面AB1E1与平面BEC1的距离为 .
16.函数 ,其中P、M为实数集R的两个非空子集,又规
定f(P)={yy=f(x),xP},f(M)={yy=f(x),xM}.给出下列四个判断,①若P∩M=Ø,则f(P)∩f(M)= Ø ②若P∩M≠Ø,则f(P)∩f(M)≠Ø ③若P∪M=R,则f(P)∪f(M)=R ④若P∪M≠R,则f(P)∪f(M)≠R,其中正确的判断为 .
答案
1.B 2.D 3.B 4.A 5.A 6.C 7.C 8.B 9.A 10.A 11.D 12.B
![]() 13.144 14.2 15. 16.②④
13.144 14.2 15. 16.②④
三基小题训练三十九
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的4个选项中,只有1项
是符合题目要求的.)
1.已知集合A={0,2,3},B={xx=a·b,a、bA},则B的子集的个数是 ( )
A.4 B.8 C.16 D.15
2.函数y=x2+1(x≤0)的反函数的大致图象为 ( )
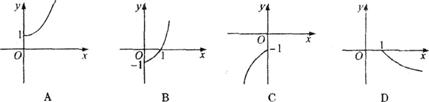 |
3.已知{an}为等差数列,{bn}为等比数列,其公比q≠1,且bi>0(i=1,2,3,…,n),若a1=b1,a11=b11,则 ( )
A.a6=b6 B.a6>b6 C.a6<b6 D.a6>b6或a6<b6
![]() 4.已知
p,q夹角为 ,则以a=5p+2q,b=p-3q为邻边的平行四边形的一条对角线长为
( )
4.已知
p,q夹角为 ,则以a=5p+2q,b=p-3q为邻边的平行四边形的一条对角线长为
( )
![]() A.15
B.
C.14
D.16
A.15
B.
C.14
D.16
![]() 5.已知a>0,函数f(x)=x3-ax在 上是单调增函数,则a的最大值是
( )
5.已知a>0,函数f(x)=x3-ax在 上是单调增函数,则a的最大值是
( )
A.0 B.1 C.2 D.3
6.二项式 的展开式中含有x4的项,则n的一个可能值是 ( )
A.1 B.3 C.6 D.10
7.设a、b是两条不同的直线,α、β是两个不同的平面,则下列四个命题:
①若a⊥b,a⊥α,则b∥α ②若a∥α,α⊥β,则a⊥β
③a⊥β,α⊥β,则a∥α ④若a⊥b,a⊥α,b⊥β,则α⊥β
其中正确的命题的个数是 ( )
A.0个 B.1个 C.2个 D.3个
![]() 8.使函数
是奇函数,且在 上是减函数的θ的一个值是( )
8.使函数
是奇函数,且在 上是减函数的θ的一个值是( )
A. B. C. D.
9.设F1、F2是双曲线 的两个焦点,P在双曲线上,当ΔF1PF1的面积为1时,
的值为
![]()
A.0 B.1 C. D.2
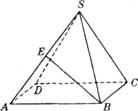
![]()
![]() 10.如图所示,已知正四棱椎S—ABCD侧棱长为 ,底面边长为 ,
10.如图所示,已知正四棱椎S—ABCD侧棱长为 ,底面边长为 ,
E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
A.90° B.60°
C.45° D.30°
11.已知函数y=f(x)(xR)满足f(x+1)=f(x-1),且x[-1,1]时,f(x) =x2,
则y=f(x)与log5x的图象的交点的个数为 ( )
A.3个 B.4个 C.5个 D.6个
12.已知三个不等式x2-4x+3<0①,x2-6x+8<0②,2x2-9x+m<0③,要使同时满足①和②的所有χ的值都满足③,则实数m的取值范围是 ( )
A.m>9 B.m=9 C.m≤9 D.0<m≤9
答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题共4个小题,每小题4分,共16分,把答案填在题中的横线上。)
13.已知两变量x、y之间的关系为lg(y-x)=lgy-lgx,则以x为自变量的函数y的最小值为 。
14.已知圆 与抛物线 的准线相切,则m= .
15.若A是ΔABC的一个内角,且 则 .
16.用砖砌墙,第一层(底层)用去了全部砖块的一半多一块,第二层用去了剩下的一半多一块,…,依次类堆,每一层都用去了上层剩下的砖块的一半多一块,如果到第九层恰好砖块用完,那么一共用了 块砖。
三基小题训练四十
命题:王统好
一、选择题(本大题共12小题,每小题5分,共60分)
1、满足条件φ⊊ M ⊊{0,1,2}的集合M共有
A、3个 B、6个 C、7个 D、8个
2、设集合M={x x= + , k∈z},N={x x= kπ± , k∈z},则M与N之间的关系是
A、M⊆N B、M⊇N C、M = N D、M≠N
3、下列四组函数中,表示同一个函数的是
A、f(x) = x 与g(x) = B、y = x°与y = 1
C、y = x+1与y = D、y = x-1 与y =
![]() 4、设函数f (x)
= 2-x-1 x≤0若f (x0) > 1,则x0的取值范围是
4、设函数f (x)
= 2-x-1 x≤0若f (x0) > 1,则x0的取值范围是
x x>0
A、(-1,1) B、(-1,+∞)
C、(-∞,-2)∪(0,+∞) D、(-∞,-1)∪(1,+∞)
5、函数y = ln x∈(1,+∞)的反函数为
A、y = x∈(0,+∞) B、y = x∈(0,+∞)
C、y = x∈(-∞,0) D、y = x∈(-∞,0)
6、函数 f (x) = x x+a +b是奇函数的充要条件是
A、ab = 0 B、a+b = 0 C、a = b D、a2+b2 = 0
7、函数y = 1-
A、在(-1,+∞)内单调递增 B、在(-1,+∞)内单调递减
C、在(1,+∞)内单调递减 D、在(1,+∞)内单调递增
8、不等式(1+x) (1-x ) > 0的解集是
A、{x 0≤x≤1} B、{x x<0且x≠-1}
C、{x -1<x<1} D、{x x<1且x≠-1}
9、当x∈R时,f (x)满足f (x+2) = f (-x+2),如果方程f(x) = 0,恰好有4个不同的实根,这四个根的和为
A、0 B、2 C、4 D、8
10、设y = x+m和y = nx-6互为反函数,则m , n值分别为
A、2 ,3 B、3,2 C、-6,3 D、3,-6
11、若函数f(x) = 的定义域为R,则实数m的取值范围是
A、(-∞,+∞) B、[ 0,) C、(,+∞) D、[ 0,]
12、设f(a) , g(x)都是单调函数,有如下四个命题
①若f(x)单调递增,g(x)单调递增,则f(x)-g(x)单调递增
②若f(x)单调递增,g(x)单调递减,则f(x)-g(x)单调递增
③若f(x)单调递减,g(x)单调递增,则f(x)+g(x)单调递减
④若f(x)单调递减,g(x)单调递减,则f(x)+g(x)单调递减
其中正确的是命题是
A、①② B、①④ C、②③ D、②④
选择题答题卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本题共4小题,每小题4分,共16分)
13、函数y = 的定义域是________________________。
14、已知全集U = {1,2,3,4,5}, A∩B= {2},(CUA)∩B = {1,4},则CUB = __________________。
15、已知f(x) = (1-) = x,则f(x) = ____________________。
16、f(x) = ,则f(1) + f(2) + f() + f(3) +f() … + f(100) + f() = ___________________。