高考数学二轮复习三角函数图象与性质考点透析
【考点聚焦】
考点1：函数y=Asin(
的图象与函数y=sinx图象的关系以及根据图象写出函数的解析式
考点2：三角函数的定义域和值域、最大值和最小值；
考点3：三角函数的单调区间、最小正周期和三角函数图象的对称轴问题；
【考题形式】1。由参定形，由形定参。2。对称性、周期性、奇偶性、单调性
【考点小测】
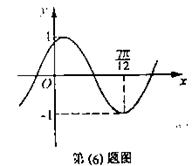1.（安徽卷）将函数
的图象按向量
平移，平移后的图象如图所示，则平移后的图象所对应函数的解析式是
A．
B．
C．
D．
解：将函数的图象按向量
平移，平移后的图象所对应的解析式为
，由图象知，
，所以
，因此选C。
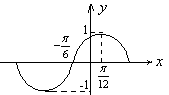2.（四川卷）下列函数中，图象的一部分如右图所示的是
（A）
（B）
（C）
（D）
解析：从图象看出，
T=
，所以函数的最小正周期为π，函数应为y=
向左平移了
个单位，即
=
，选D.
3．2007年广东5.
A.周期为
的奇函数；B. 周期为的偶函数 C.周期为
的奇函数D.周期为的偶函数
4．（湖南卷）设点P是函数
的图象C的一个对称中心，若点P到图象C的对称轴上的距离的最小值
，则
的最小正周期是
A．2π B. π C. 
D.
解析：设点P是函数的图象C的一个对称中心，若点P到图象C的对称轴上的距离的最小值，∴ 最小正周期为π，选B.
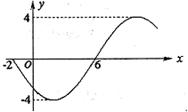
5．（天津卷）函数
的部分图象如图所示，则函数表达式为（A ）
（A）
（B）
（C）
（D）
6（天津卷）要得到函数
的图象，只需将函数
的图象上所有的点的（C）
(A)横坐标缩短到原来的
倍（纵坐标不变）,再向左平行移动
个单位长度
(B)横坐标缩短到原来的倍（纵坐标不变），再向右平行移动
个单位长度
(C)横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动个单位长度
(D)横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动个单位长度
7．（全国卷I）设函数
。若
是奇函数，则
__________。
解析：
，则
=
为奇函数，∴ φ=
.
8．（湖南卷）若
是偶函数，则a= .
解析：
是偶函数，取a=－3，可得
为偶函数。
| 小测题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答 案 | C | D | A | B | A | C |
| －3 |
【典型考例】
★例1★.（2006福建卷）已知函数f(x)=sin2x+
sinxcosx+2cos2x,x
R.
（I）求函数f(x)的最小正周期和单调增区间；
（Ⅱ）函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到？
本小题主要考查三角函数的基本公式、三角恒等变换、三角函数的图象和性质等基本知识，以及推理和运算能力。满分12分。
解：（I）
的最小正周期
由题意得
即 
的单调增区间为
（II）方法一： 先把
图象上所有点向左平移
个单位长度，得到
的图象，再把所得图象上所有的点向上平移
个单位长度，就得到
的图象。
方法二：把图象上所有的点按向量
平移，就得到的图象。
★例2★（2007全国）设函数
图像的一条对称轴是直线
。（Ⅰ）求
；（Ⅱ）求函数
的单调增区间；（Ⅲ）画出函数在区间
上的图像。
本小题主要考查三角函数性质及图像的基本知识，考查推理和运算能力，满分12分.
解：（Ⅰ）
的图像的对称轴，
（Ⅱ）由（Ⅰ）知
由题意得 
所以函数
（Ⅲ）由
| x | 0 |
|
|
|
|
|
| y |
| －1 | 0 | 1 | 0 |
|
|
★例3★.已知函数f(x)=A
(A>0,
>0,0<
<
函数，且y=f(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）.
（1）求f(x);
（2）计算f(1)+f(2)+… +f(2 008).
解：（I）
的最大值为2，
.
又
其图象相邻两对称轴间的距离为2，
，
.
过
点，
又
.
（II）解法一：
，
.
又的周期为4，
，
解法二：
又
的周期为4，，
★例4★（2006湖北）设函数
，其中向量
，
，
，
。
（Ⅰ）、求函数
的最大值和最小正周期；
（Ⅱ）、将函数的图像按向量
平移，使平移后得到的图像关于坐标原点成中心对称，求长度最小的。
【课后训练】
一选择题.
1．（全国卷I）函数
的单调增区间为
A．
B．
C．
D．
2.（全国II）若f(sinx)＝3－cos2x，则f(cosx)＝
（A）3－cos2x （B）3－sin2x （C）3＋cos2x （D）3＋sin2x
3.（浙江卷）函数y=sinx+sin
x,x
的值域是
(A)［-,］ (B)［-,］ (C)［
］ (D)［
］
4.（天津卷）已知函数
（
、
为常数，
，
）在
处取得最小值，则函数
是（ ）
A．偶函数且它的图象关于点
对称 B．偶函数且它的图象关于点
对称
C．奇函数且它的图象关于点对称 D．奇函数且它的图象关于点对称
5当
时，函数
的最小值是（ ）
6.（北京卷）对任意的锐角α，β，下列不等关系中正确的是
（A）sin(α+β)>sinα+sinβ （B）sin(α+β)>cosα+cosβ
（C）cos(α+β)<sinα＋sinβ （D）cos(α+β)<cosα＋cosβ
7.（全国卷Ⅱ）已知函数y =tan 
在（-
，）内是减函数，则
（A）0 < 
≤
1 （B）-1 ≤ < 0 （C）≥ 1 （D）≤ -1
8．（湖北卷）若
（ ）
A．
B．
C．
D．
9．（山东卷）函数
，若
，则的所有可能值为（ ） （A）1 （B）
（C）
（D）
10.（上海卷）函数
的图象与直线
有且仅有两个不同的交点，则
的取值范围是__________。
11.（湖北卷）函数
的最小正周期与最大值的和为
.
12.（重庆卷）已知
、
均为锐角，且
=
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | C | D | D | B | A | C | B | 1<k<3 |
| 1 |
二．解答题
1.（广东卷）已知函数
.(I)求
的最小正周期；
(II)求的的最大值和最小值；(III)若
，求
的值.
解：
（Ⅰ）的最小正周期为
; （Ⅱ）的最大值为
和最小值
；
（Ⅲ）因为
，即
,即 
2．已知函数
。
（1）求的最小正周期、的最大值及此时x的集合；
（2）证明：函数的图像关于直线
对称。
解：
(1)所以的最小正周期
，因为，
所以，当
，即
时，最大值为
；
(2)证明：欲证明函数的图像关于直线对称，只要证明对任意，有
成立，
因为
，
，
所以成立，从而函数的图像关于直线对称。
3.（上海春）已知函数
.
（1）若
，求函数的值； （2）求函数的值域.
解：（1）
，
.
（2）
， 
，
函数的值域为
.
4.(重庆卷)设函数f(x)=cos2ωx+sinxcosx+a(其中＞0,a
R),且f(x)的图象在y轴右侧的第一个高点的横坐标为
.（Ⅰ）求ω的值；（Ⅱ）如果f(x)在区间
上的最小值为，求a的值.
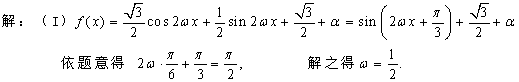
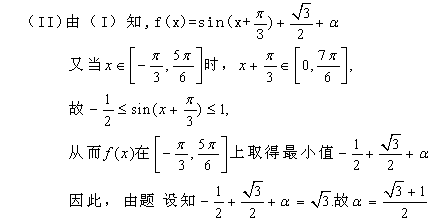
5．已知函数
（Ⅰ）将f(x)写成
的形式，并求其图象对称中心的横坐标；
（Ⅱ）如果△ABC的三边a、b、c满足b2=ac，且边b所对的角为x，试求x的范围及此时函数f(x)的值域.
解：
（Ⅰ）由
=0即
即对称中心的横坐标为
（Ⅱ）由已知b2=ac
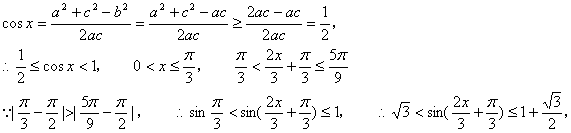即的值域为
.
综上所述，
，
值域为 .
说明：本题综合运用了三角函数、余弦定理、基本不等式等知识，还需要利用数形结合的思想来解决函数值域的问题，有利于培养学生的运算能力，对知识进行整合的能力。
6． 已知函数y=cos2x+
sinx·cosx+1 （x∈R）,
（1）当函数y取得最大值时，求自变量x的集合；
（2）该函数的图像可由y=sinx(x∈R)的图像经过怎样的平移和伸缩变换得到？
解：（1）y=cos2x+sinx·cosx+1= (2cos2x－1)+ +
（2sinx·cosx）+1
=cos2x+sin2x+
=(cos2x·sin
+sin2x·cos)+
=sin(2x+)+
所以y取最大值时，只需2x+=
+2kπ,（k∈Z），即
x=+kπ,（k∈Z）。
所以当函数y取最大值时，自变量x的集合为{xx=+kπ,k∈Z}
（2）将函数y=sinx依次进行如下变换：
（i）把函数y=sinx的图像向左平移，得到函数y=sin(x+)的图像；
（ii）把得到的图像上各点横坐标缩短到原来的倍（纵坐标不变），得到函数y=sin(2x+)的图像；
（iii）把得到的图像上各点纵坐标缩短到原来的倍（横坐标不变），得到函数y=sin(2x+)的图像；
（iv）把得到的图像向上平移个单位长度，得到函数y=sin(2x+)+的图像。
综上得到y=cos2x+sinxcosx+1的图像。