高考数学三角函数
考试要求：1、理解任意角的概念、弧度的意义。能正确地进行弧度与角度的换算。2、掌握任意角的正弦、余弦、正切的定义。了解余切、正割、余割的定义。掌握同角三角函数的基本关系式。掌握正弦、余弦的诱导公式。了解周期函数与最小正周期的意义。3、掌握两角和与两角差的正弦、余弦、正切公式。掌握二倍角的正弦、余弦、正切公式。4、能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明。5、了解正弦函数、余弦函数、正切函数的图象和性质，会用“五点法”画正弦函数、余弦函数和函数
的简图，理解
的物理意义。6、会由已知三角函数值求角，并会用符号
、
、
表示。7、掌握正弦定理、余弦定理，并能初步运用它们解斜三角形。
1、已知
等于：
A．
B．
C．
D．
2、已知α、
都是第二象限角，且
，则：
A．
B．
C．
D．
3、若
=
.
4、下列函数中周期为2的是：
A．
B．
C．
D．
5、在△ABC中，A = 15°，则
的值为：
A．
B．
C．
D．2
6、定义的R上的偶函数
上是减函数，
是锐角三角形的两个内角，则：
A.
B.
C.
D.
7、若
的最大值为：
A．
B．
C．
D．不存在
8、锐角三角形ABC中，a、b、c分别是三内角A、B、C的对边. 设B=2A，则
的取值范
围是：
A．（－2，2） B．（0，2） C．（，2） D．（
）
9、同时具有性质“①最小正周期是
；②图象关于直线
对称；③在
上是增函数”的一个函数是：
A.
B.
C .
D.
10、关于函数
有下列判断：①是偶函数；②是奇函数；③是周期函数；④不是周期函数，其中正确的是：
A．①与④ B．①与③ C．②与④ D．②与③
11、设函数
，若对于任意实数x，有
，
则下列说法正确的是：
A．这样的ω有且只有一个，且ω=2 B．这样的ω有无数多个，其中最小的ω=3
C．这样的ω有且只有一个，且ω=3 D．这样的ω有无数多个，其中最小的ω=2
12、要得到函数
的图象，只需将函数
的图象做以下平移得到：
A．按向量
平移 B．按向量
平移
C．按向量
平移 D．按向量
平移
13、若
是纯虚数，则
的值为：
A.
B.
C.
D.
14、直线
的倾斜角为
，且sin+cos= 0，则a，b满足 :
A．
B．
C．
D．
15、设函数，
若对任意x∈R，都有，f (x1 )≤f (x )≤f (x2 )成立，则x1 —x2的最小值为 ( )
A. 4
B. 2
C. 1
D. 
16、已知
则实数a的取值范围
是:
A．
B．
C．
D．
17、函数
上最大值等于：
A．
B．
C．
D．
18、函数
在［0，
］上取得最大值时，x的值为
A. 0 B.
C.
D.
19、设函数
，给出下列四个论断：
①它的周期为
； ②它的图象关于直线
对称；
③它的图象关于点（，0）对称； ④在区间（
，0）上是增函数。
请以其中两个论断为条件，另两个论断为结论，写出一个你认为正确的命题：
__________________________________________________（用序号表示）
20、已知函数
（1）设
>0为常数，若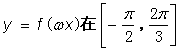
上是增函数，求的取值范围；
（2）设集合
,B=
若A 
B，求实数m的取值范围.
21、在△ABC中，角A、B、C的对边分别为a、b、c，△ABC的外接圆半径
，且
满足
（Ⅰ）求角B和边b的大小；（Ⅱ）求△ABC的面积的最大值.
四、三角函数参考答案
1、A；2、B；3、2003；4、C；5、C；6、D；7、C；8、D；9、C；10、B；11、D
12、B；13、B；14、D；15、B；16、C；17、D；18、B；19、①②
③④
20、解：（1）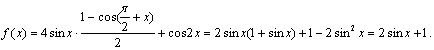
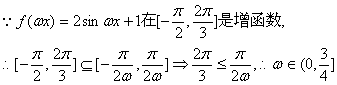
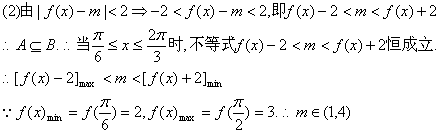
21．解：（Ⅰ）由已知
，
整理得，
即
∵A+B+C=180°，∴
，
∴sinA=2sinAcosB，又∵
，
∵
∴B=60°， b=3
（Ⅱ）由余弦定理，得 
∴
，
即ac≤9，（当a=c=3时，取“=”），
∴
，
△ABC的面积的最大值为