综合模拟测试(一)
一、选择题
1.集合![]() ,已知
,已知![]() 只有一个子集,那么实数
只有一个子集,那么实数![]() 的取值范围是
(
)
的取值范围是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.曲线![]() 的长度是 (
)
的长度是 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.不等式![]() 的解集是 (
)
的解集是 (
)
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.把函数![]() 的图象沿向量
的图象沿向量![]() 的方向平移后,所得的图象关于
的方向平移后,所得的图象关于![]() 轴对称,则
轴对称,则![]() 的最小值是
( )
的最小值是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.等差数列![]() 的公差为
的公差为![]() ,前
,前![]() 项的和为
项的和为![]() ,当首项
,当首项![]() 变化时,
变化时, ![]() 是一个定值,则下列各数中也为定值的是
( )
是一个定值,则下列各数中也为定值的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.一椭圆以正三角形![]() 的顶点
的顶点![]() 为焦点,且过
为焦点,且过![]() 的中点,则其离心率是( )
的中点,则其离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.半径为4的球面上有![]() 四点,且
四点,且![]() ,则
,则![]() 的最大值为(
的最大值为(![]() 表示三角形面积) (
)
表示三角形面积) (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.某校有6间不同的电脑室,每天晚上至少开放2间,欲求不同的安排方案的种数,现有四位同学分别给出下列四个结果:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是
(
)
.其中正确的结论是
(
)
A.仅有① B.②和④ C.②和③ D.仅有③
9.已知函数![]() 上任一点
上任一点![]() 处的切线斜率
处的切线斜率![]() ,则该函数的单调减区间为
(
)
,则该函数的单调减区间为
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.对任意![]() ,奇函数
,奇函数![]() 和偶函数
和偶函数![]() 在区间
在区间![]() 上的图象关于
上的图象关于![]() 轴对称,且
轴对称,且![]() 为增函数,则下列各选项中能使不等式:
为增函数,则下列各选项中能使不等式: ![]() 成立的是( )
成立的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
11.已知条件![]() ,条件
,条件![]() .若
.若![]()
![]() 是
是![]()
![]() 的必要不充分条件,则实数
的必要不充分条件,则实数![]() 的取值范围是________.
的取值范围是________.
12.![]() ,若
,若![]() 的图象向左至少平移
的图象向左至少平移![]() 个长度单位后所得的图象恰为奇函数的图象,而向右至少平移
个长度单位后所得的图象恰为奇函数的图象,而向右至少平移![]() 个长度单位后所得的图象恰为偶函数的图象,则
个长度单位后所得的图象恰为偶函数的图象,则![]() 的最小正周期是________.
的最小正周期是________.
13.设满足![]() 的点
的点![]() 的集合为
的集合为![]() ,满足
,满足![]() 的点
的点![]() 的集合为
的集合为![]() ,则
,则![]() 所表示的图形的面积是________.
所表示的图形的面积是________.
14.已知![]() ,且
,且![]() 都是正数,则
都是正数,则![]() 的最小值是________.
的最小值是________.
15.一项
“过关游戏”规则规定:在第![]() 关要抛掷一颗骰子
关要抛掷一颗骰子![]() 次,如果这
次,如果这![]() 次抛掷所出现的点数之和大于
次抛掷所出现的点数之和大于![]() ,则算过关,那么连过前二关的概率是________.
,则算过关,那么连过前二关的概率是________.
16.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数![]() 的图象恰好通过
的图象恰好通过![]() 个格点,则称函数
个格点,则称函数![]() 为
为![]() 阶格点函数.下列函数:①
阶格点函数.下列函数:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中是一阶格点函数的有_______.
,其中是一阶格点函数的有_______.
三、解答题
17.已知![]() 三点的坐标分别是
三点的坐标分别是![]() ,其中
,其中![]() .
.
(1)若![]() ,求角
,求角![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
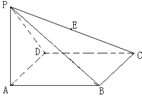 18.如图,四棱锥
18.如图,四棱锥![]() 的底面为菱形,且
的底面为菱形,且![]() ,
,
![]() ,
,![]() 的中点.
的中点.
(1)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)求二面角![]() 的平面角的正切值;
的平面角的正切值;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 成立?如果存在,求出
成立?如果存在,求出![]() 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
19.设平面向量![]() (其中
(其中![]() ),且
),且![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)若函数![]() 对任意
对任意![]() 都有
都有![]() ,求此时
,求此时![]() 在
在![]() 上的最小值;
上的最小值;
(3)若点![]() 在不等式
在不等式![]() 所表示的区域内,且
所表示的区域内,且![]() 为方程
为方程![]() 的一个解,当
的一个解,当![]() 时,请判断
时,请判断![]() 是否为方程
是否为方程![]() 的根,并说明理由.
的根,并说明理由.
20.设椭圆![]() 的两个焦点是
的两个焦点是![]() ,且椭圆上存在点
,且椭圆上存在点![]() ,使
,使![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若直线![]() 与椭圆存在一个公共点
与椭圆存在一个公共点![]() ,使得
,使得![]() 取得最小值,求此最小值及此时椭圆的方程;
取得最小值,求此最小值及此时椭圆的方程;
(3)在条件(2)下的椭圆方程,是否存在斜率为![]() 的直线
的直线![]() ,与椭圆交于不同的两点
,与椭圆交于不同的两点![]() ,满足
,满足![]() ,且使得过点
,且使得过点![]() 两点的直线
两点的直线![]() 满足
满足![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
21.已知函数![]() ,其中
,其中![]() .
.
(1)设![]() 在
在![]() 处取得极值,其中
处取得极值,其中![]() ,求证:
,求证: ![]() ;
;
(2)设![]() ,求证:线段
,求证:线段![]() 的中点
的中点![]() 在曲线
在曲线![]() 上;
上;
(3)若![]() ,求证:过原点且与曲线
,求证:过原点且与曲线![]() 相切的两条直线不可能垂直.
相切的两条直线不可能垂直.
答案
一、选择题
1.A 2.A 3.D 4.C 5.C 6.D 7.C 8.C 9.B 10.A
二、填空题
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.
15.![]() 16.①②④
16.①②④
三、解答题
17.解:(1) ![]() .
.
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
化简得![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
(2) ![]() ,
,
![]() ,
,
∴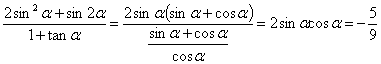 .
.
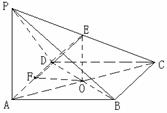 18.解:(1)如图,连
18.解:(1)如图,连![]() ,则由
,则由![]() ,得平面
,得平面![]() .
.
又由底面![]() 为菱形,可得
为菱形,可得![]() ,所以
,所以![]() .
.
连![]() ,则
,则![]() 为
为![]() 在平面
在平面![]() 上的射影,所以
上的射影,所以![]() 即为
即为![]() 与平面
与平面![]() 所成的角.
所成的角.
由![]() 中点可得
中点可得![]() .
.
又由菱形性质可得,在![]() 中,
中, ![]() ,所以
,所以![]() .
.
所以在![]() 中,
中,![]() ,所以
,所以![]() .
.
(2)由![]() ,
,![]() ,可得
,可得![]() .
.
过![]() 作
作![]() ,连
,连![]() ,则由三垂线定理可得
,则由三垂线定理可得![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
由(1)可知![]() ,又在
,又在![]() 中,
中, ![]() ,
,
所以![]() ,所以
,所以![]() .
.
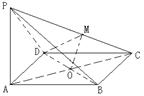 (3)设
(3)设![]() ,过
,过![]() 作
作![]() ,则由
,则由![]() 可得平面
可得平面![]() .
.
又![]() ,所以
,所以![]() .
.
所以![]() ,而
,而![]() ,可得
,可得![]() ,故线段
,故线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 成立,
成立, ![]() .
.
19.解:(1)∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)已知对任意的![]() 都有
都有![]() ,
,
∴当![]() 时有
时有![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() 上是增函数, ∴
上是增函数, ∴![]() ,
,
∴![]() 上的最小值为
上的最小值为![]() .
.
(3)设![]() ,由
,由![]() 知
知![]() ,
,
∴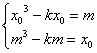

由①-②得![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 是方程
是方程![]() 的根.
的根.
20.解:(1)由椭圆定义可得![]() ,
,
由![]() 可得
可得![]() ,
,
而![]() ,∴
,∴![]() ,解得
,解得![]() .
.
(2)由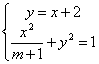 ,得
,得![]() ,
,
![]() ,
,
解得![]() (舍去),∴
(舍去),∴![]() .
.
此时![]() .
.
当且仅当![]() 时,
时, ![]() 取得最小值
取得最小值![]() ,此时椭圆方程为
,此时椭圆方程为![]() .
.
(3)由![]() 知点
知点![]() 是
是![]() 的中点.
的中点.
设![]() 两点的坐标分别为
两点的坐标分别为![]() ,中点
,中点![]() 的坐标为
的坐标为![]() ,
,
则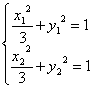 ,两式相减得
,两式相减得![]() .
.
∴![]() ,∴
,∴![]() 中点
中点![]() 的轨迹为直线
的轨迹为直线![]() ①且在椭圆内的部分.
①且在椭圆内的部分.
又由![]() 可知
可知![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,方程为
,方程为![]() ②
②
①、②联立可求得点![]() 的坐标为
的坐标为![]() ,∵点
,∵点![]() 必在椭圆内,∴
必在椭圆内,∴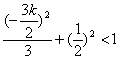 ,
,
解得![]() ,又∵
,又∵![]() ,∴
,∴![]() .
.
21.解:(1)![]() ,∴
,∴![]() 的两根为
的两根为![]() ,
,
令![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
故有![]() .
.
(2)设![]() 中点
中点![]() ,则
,则![]() ,
,
故有![]() ,∴
,∴![]() ,
,
![]() .
.
∴![]() .
.
代入验算可知![]() 在曲线
在曲线![]() 上.
上.
(3)过曲线上的点![]() 的切线的斜率是
的切线的斜率是![]() ,
,
当![]() 时,切线的斜率
时,切线的斜率![]() ;
;
当![]() 时,
时, ![]() ,∴
,∴![]() ,
,
∴切线斜率![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,故过原点且与曲线相切的两条直线不可能垂直.
,故过原点且与曲线相切的两条直线不可能垂直.