综合模拟测试(三)
第Ⅰ卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内.
1. 某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,
现用分层抽样的方法从该校所有高中生中抽取一个容量为45的样本,那么高一、高二、高三年级抽取的人数分别为 ( )
A. 15,5,25 B.15,15,15
C.10,5,30 D.15,10,20
2.设![]() 、
、![]() 是不同的直线,
是不同的直线,![]() 、
、![]() 、
、![]() 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() ; (4)
; (4)![]() .
.
其中,假命题是( )
A.(1)(2) B.(2)(3) C.(1)(3) D.(2)(4)
3.( 06年天津卷)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有( )
A.10种 B.20种 C.36种 D.52种
4.若直线![]() 按向量
按向量![]() 平移后与圆
平移后与圆![]() 相切,则
相切,则![]() 的值为( )
的值为( )
A.14或-6 B.12或-8 C.8或-12 D.6或-14
5.竖在地面上的两根旗杆的高分别为10米和15米,相距20米.则地面上到两旗杆顶点的仰角相等的点P的轨迹是( )
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
6.设![]() 是函数
是函数![]() 的反函数,若
的反函数,若![]() ,则
,则
![]() 的值为 ( )
的值为 ( )
A.1 B.2 C.3 D.![]()
7.已知函数![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
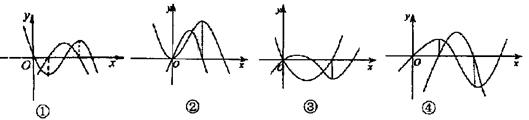
8.下面四图都是同一坐标系中某三次函数及其导函数的图象,其中一定不正确的序号是( )
|
A.①、② B.③、④ C.①、③ D.①、④
9.在△ABC中,![]() 、
、![]() 、
、![]() 分别是角
分别是角![]() 所对的边,
所对的边,![]() 60º,
60º,![]() ,△
,△![]() 的面积
的面积![]() =
=![]() ,则
,则![]() 的值等于( )
的值等于( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10. 等差数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,则过点
,则过点![]() 和
和
![]() 的直线的一个方向向量的坐标可以是( )
的直线的一个方向向量的坐标可以是( )
A. (![]() ,
,![]() ) B.
) B. ![]() C.
C. ![]() D.
D.![]()
第Ⅱ卷(非选择题 共110分)
二、填空题:本大题共6小题,每小题5分,共30分.把答案填在题中横线上.
11. 在![]() 的展开式中,
的展开式中,![]() 的系数是
;各项系数的和是
.(用数字作答)
的系数是
;各项系数的和是
.(用数字作答)
12.已知![]() 满足约束条件
满足约束条件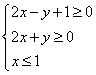 ,则
,则![]() 的最小值为
.
的最小值为
.
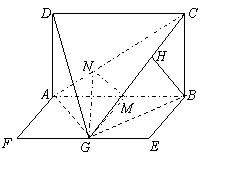
13.直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 上有一动点
上有一动点![]() ,则△
,则△![]() 周长的最小值是
.
周长的最小值是
.
14.10张奖券中只有3张有奖,5个人购买,至少有1人中奖的概率是 .
15.已知![]() 为坐标原点,点
为坐标原点,点![]() 在单位圆
在单位圆![]() 上,点
上,点![]() 满足
满足![]() ,则
,则![]() .
.
16.对于在区间![]() 上有意义的两个函数
上有意义的两个函数![]() 与
与![]() ,如果对于任意
,如果对于任意![]() ,均有
,均有
![]() ,则称
,则称![]() 与
与![]() 在
在![]() 上是接近的. 若函数
上是接近的. 若函数![]() 与函数
与函数![]() 在区间
在区间![]() 上是接近的,给出如下区间①[1,4];②[1,3];③[1,2]∪[3,4];④
上是接近的,给出如下区间①[1,4];②[1,3];③[1,2]∪[3,4];④![]() .则区间
.则区间![]() 可以是
.(把你认为正确的序号都填上)
可以是
.(把你认为正确的序号都填上)
三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)已知箱子中有10个球,其中8个是正品,2个是次品,若每次取出1个球,取出后不放回,求:
(I)取两次就能取到2个正品的概率;
(II)取三次才能取到2个正品的的概率;
(Ⅲ)取四次才能取到2个正品的的概率.
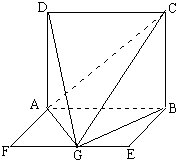 18.(本小题满分14分)如图,平面
18.(本小题满分14分)如图,平面![]() ⊥平面
⊥平面![]() ,
,![]() 是正方形,
是正方形,![]() 是矩形,
是矩形,![]() 是线段
是线段![]() 的中点,且
的中点,且![]() 点在平面
点在平面![]() 内的射影在
内的射影在![]() 上.
上.
(1)求证:![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
19.(本小题满分14分)
某厂有一台价值为1万元的生产设备,现要通过技术改造来提高该生产设备的生产能力,提高产品的增加值,经过市场调查,产品的增加值y万元与技术改造投入金额x万元之间满足:①y与![]() 和
和![]() 的乘积成正比;②当
的乘积成正比;②当![]() 时,
时,![]() . 并且技术改造投入的金额满足;
. 并且技术改造投入的金额满足;![]() ,其中t为常数.
,其中t为常数.
(1)求![]() 的解析式及定义域;
的解析式及定义域;
(2)当![]() 时,求产品的增加值的最大值及相应的技术改造投入的金额.
时,求产品的增加值的最大值及相应的技术改造投入的金额.
20.(本小题满分14分)
双曲线的中心是原点O,它的虚轴长为![]() ,相应于焦点
,相应于焦点![]()
![]() 的准线l与x轴交于点A,且
的准线l与x轴交于点A,且![]() .过点F的直线与双曲线交于P、Q两点.
.过点F的直线与双曲线交于P、Q两点.
(Ⅰ)求双曲线的方程及离心率;
(Ⅱ)若![]() ,求直线PQ的方程.
,求直线PQ的方程.
21.(本小题满分16分)
已知定义在R上的单调函数![]() ,存在实数
,存在实数![]() ,使得对于任意实数
,使得对于任意实数![]() 总有
总有
![]() 恒成立.
恒成立.
(1)求![]() 的值;
的值;
(2)若![]() ,且对任意正整数n,有
,且对任意正整数n,有![]() ,记
,记
![]() ,比较
,比较![]() 与Tn的大小关系,并给出证明.
与Tn的大小关系,并给出证明.
高三数学模拟试卷(三)参考答案
1. D提示:按比例抽取
2.D 提示:发挥空间想象
3.A提示:分类讨论的思想
4.A提示:圆心到平移后的直线的距离等于半径
5.A提示:即点P到两个定点的距离之比为常数,易知点P的轨迹是圆
6.B提示:![]() ,
,![]()
7.B 提示:![]() 就是
就是![]() 的展开式中
的展开式中![]() 前面的系数
前面的系数
8.B提示:导函数的零点就是三次函数的极值点,且当三次函数的单调增区间所对应的导函数的函数值为正
9.C提示:先求出![]() 边的长,再求
边的长,再求![]() 边的长
边的长
10. B 提示:由![]() 及
及![]() 求出公差
求出公差![]() ,再求出直线
,再求出直线![]() 的斜率,从而得到它的方向向量
的斜率,从而得到它的方向向量
11.40;243提示:![]() 的系数是
的系数是![]() ,在
,在![]() 中令
中令![]() 就可得到各项系数的和
就可得到各项系数的和
12.![]() 提示:画出图形
提示:画出图形
13.![]() 提示:在△
提示:在△![]() 中
中![]() 是个定值,要使△
是个定值,要使△![]() 周长的最小值,即把
周长的最小值,即把![]() 翻折到平面
翻折到平面![]() 中,且使得
中,且使得![]() 、
、![]() 、
、![]() 在一直线上
在一直线上
14.![]() 提示:
提示:![]()
15.![]() 提示:先算出
提示:先算出![]() ,再用余弦定理算出
,再用余弦定理算出![]() 与
与![]() 的夹角,最后用数量积公式
的夹角,最后用数量积公式
16.③、④提示:由题意得![]() ,然后算它在各给定区间上的最大值,只要最大值小于或等于1就满足条件
,然后算它在各给定区间上的最大值,只要最大值小于或等于1就满足条件
17. (I)取两次就能取到2个正品的概率为:![]() =
=![]() .
.
(II)取三次才能取到2个正品的概率为:![]() =
=![]() .
.
(Ⅲ)取四次才能取到2个正品的概率为:![]() =
=![]() .
.
18.(1)设![]() 点在平面
点在平面![]() 内的射影为
内的射影为![]() ,则
,则![]() 在CG上,由
在CG上,由![]() ⊥平面
⊥平面![]() ,知
,知![]() ⊥
⊥![]() ,∵
,∵![]() 为正方形,∴
为正方形,∴![]() ,又平面
,又平面![]() ⊥平面
⊥平面![]() ,∴
,∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,∴
,∴![]()
 ,又
,又![]() 、
、![]()
![]() 平面
平面![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ;
;
(2)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,连
,连![]() ,∵平面
,∵平面![]() ⊥平面
⊥平面![]() ,
,![]() ,∴
,∴![]() ⊥平面
⊥平面![]() ,又
,又![]() ⊥
⊥![]() ,
,
∴![]() ⊥
⊥![]() ,∴
,∴![]() 就是二面角
就是二面角![]() 的平面角,在平面
的平面角,在平面![]() 内,由
内,由![]() 是矩形,
是矩形,![]() 是
是![]() 的中点,
的中点,![]() ,可得
,可得![]() 是
是![]() 的中点,又∵
的中点,又∵![]() ⊥平面
⊥平面![]() ,∴
,∴![]() ,∴
,∴![]() ,设
,设![]() ,则
,则![]() ,又
,又![]() , ∴
, ∴![]()
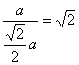 ,∴
,∴![]() ,∴二面角B-AC-G的大小为
,∴二面角B-AC-G的大小为![]() .
.
19.(1)由已知,设![]()
∵当![]()
![]()
则![]()
∵![]()
∴![]() 的定义域为
的定义域为![]()
(2)∵![]()
令![]() .
.
∵![]() 当
当![]()
![]() 上单调递增;
上单调递增;
当![]()
![]() 上单调递减.
上单调递减.
∴当![]() 时,
时,![]() 取得极大值.
取得极大值.
∵![]()
∴当![]()
∴当![]()
综上,当![]() 万元,最大增加值是
万元,最大增加值是![]() 万元.当0<t<1时,投入
万元.当0<t<1时,投入![]() 万元,最大增加值是
万元,最大增加值是![]() 万元.
万元.
20.(Ⅰ)由题意,设曲线的方程为![]() = 1(
= 1(![]() ),
),
由已知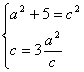 解得
解得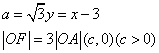 ,
,![]() .
.
所以双曲线的方程这![]() = 1离心率
= 1离心率![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,
,![]() , 当直线
, 当直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 方程为
方程为![]() .此时,
.此时, ![]() ,应舍去.
,应舍去.
当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() .
.
由方程组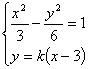 ,得
,得![]() .
.
由一过点![]() 的直线与双曲线交于
的直线与双曲线交于![]() 两点,
两点,
则![]() ,即
,即![]() ,
,
由于![]()
![]() ,即
,即![]() R.
R.
∴![]() R且
R且![]() (*) .
(*) .
设![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,
,![]() ),则
),则
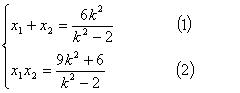 ,
,
由直线![]() 的方程得
的方程得![]() ,
,![]() ,
,
于是![]()
![]() (3)
(3)
∵![]() ,
,
∴![]()
即![]() (4),
(4),
由(1)、(2)、(3)、(4)得
![]() ,
,
整理得![]() =
=![]() .
.
∴![]() 满足(*).
满足(*).
∴直线![]() 的方程为
的方程为![]() 或
或![]() .
.
21.(1)令![]() ,得
,得![]() ①
①
令![]() ,得
,得![]() ②
②
由①,②得 ![]()
![]() 为单调函数,
为单调函数,![]()
(2)由(1)得![]() .
.
![]()
![]()
![]()
又![]()
![]()
又![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]()
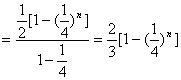 .
.
![]()
![]() ,
,
![]()