高考数学模拟试题（二）

综合模拟测试（二）

第Ⅰ卷（选择题 共50分）

一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．设，则下列不等式成立的是 　　　　　　　　　　　　　　　　　　　（　）

　　　 A．　　　 　　　　　　 B．　

C． 　　　　　　D．　　　　　　　

2．若x＞4，则函数　　　　　　　　　　　　　　　　 （　）

A．有最大值—6　　 B．有最小值6　　　 C．有最大值—2　　D．有最小值2

3．双曲线的一条渐近线与直线垂直，则双曲线的离心率为（　）

A．　　　　　　　　　 B．　　　　　　　　　　C．±　　　　　　　　D．

4．若变量x,y满足约束条件

　　　 　

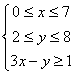
则变量z=x-y的取值情况是　　　　　　　　　　　　　　　　　　　　　 （　 ）

A．既没有最大值也没有最小值　　 B．有最大值5，没有最小值

C．有最小值-1，没有最大值　　　　D．有最小值－5，也有最大值5

5．已知m、l是直线，α、β是平面，给出下列命题　　　　　　　　　　 （　 ）

　　　 ①若l⊥α，m∥α,则l⊥m；

②若m∥l，l α则l∥α；

　　　 ③若；

④若l⊥α，则l垂直于α内的任意一条直线。

　　　 其中正确命题的个数是　　　　　　　　　　　　　　　　　　  （　）

　　　 A．1个　B．2个　C．3个　D．4个

6．AB是抛物线的一条焦点弦，AB=4，则AB中点C的横坐标是　　　　　　 （　）　

A．2　　　　　　　　　　 B．　　　　　　　　　　　 C．　　　　　　　　　　　 D．

7．棱长为a的正四面体中，高为h，斜高为m，相对棱间的距离为d，则a、m、h、d的大小关系正确的是　　　　　　 　（　 ）

　　　 A．a＞m＞h＞d　　　　　　　　　　　　　　　　　　　 B．a＞h＞m＞d

　　　 C．a＞h＞d＞m　　　　　　　　　　　　　　　　　　　 D．a＞d＞h＞m

8.在等差数列{a_n}中，a₁>0,5a₅=17a₉,则数列{a_n}前n项和s_n取最大值时，n的值等于（　）

　　　 A． 12 　　　 B．11　　　　　　　 　　　 C．10　　　 　　　　 D．9　

9．艺术体操委员会由10位女性委员与5位男性委员组成，委员会要组织6位委员出国考察学习，如果按性别作分层，并在各层依比例随机抽样，试问此考察团的组成方法的种数共有　　　　　　　　　　　 　　　　　　　（　）　　　　　　　　　　　　　　

　　　 A．　　　　　　　　B．　　　　　　　 C．　　　　　　　　　　D．

10． 若双曲线y²- x²=1与有唯一的公共点，则实数m的取值集合中元素的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

A．2　　　　　　　 B．4　 　　　　　　 C．5　　　　　　　 D．6

第Ⅱ卷（非选择题，共100分）

一.填空题：本大题共6小题，每小题4分，共24分.把答案填在题中横线上.

11．“关于x的不等式x+1>a的解集为R”的一个充分而不必要条件可以是　　　　 ．

12．的值为　　　　　  ．

13．函数y = 　x⁴ 的图象在点（，y₀）处切线的倾斜角为 　　　　　　  .

14．已知（1+x）+（1+x）²+…+（1+x）ⁿ = a₀+a₁x+…+a_nx_n ,　若a₁+a₂+…+a_n = 30 –n ,则正整数n的值为 　　　　　  .

15．将圆按向量v=（2，1）平移后，与直线相切，则λ的值为 　　　　　.

16．已知函数f(x)= 的反函数的图象的对称中心是（0，2），则a= 　　　　 .

三、解答题：本大题共5小题，共72分. 解答应写出文字说明，证明过程或演算步骤.

17．（本满分题14分）△ABC中，三个内角分别是A、B、C，向量a时，求a．

18．（本满分题14分）正三棱柱ABC—A₁B₁C₁的侧棱长和底面边长都等于2，D是BC上一点，且AD⊥BC.

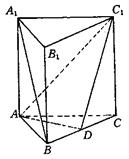
（1）试判断A₁B与平面ADC₁的位置关系，

并证明你的结论;

　　　 （2）求截面ADC₁与侧面ACC₁A₁所成的

二面角D—AC₁—C的大小.

19．（本小题满分14分）

　　　 已知函数.

　　　 （1）求函数f（x）的定义域；

　　　 （2）若函数f（x）在[10，+∞])上单调递增，求k的取值范围.

20． （本小题满分14分）

　 观察下列关于实数a、b、c的命题

①　　 若 ,则a>0,且b>0 ;

②　　 若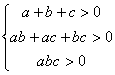　,则a、b、c均为正.

请依据命题①②的结构特征,将命题推广为关于实数a、b、c、d四个字母的形式,并证明你的结论.

21．（本小题满分14分）

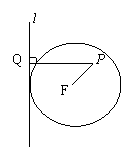　　　 如图，定直线l是半径为3的定圆F的切线，P为平面上一动点，作PQ⊥l于Q，若PQ=2PF.

　　　 （1）点P在怎样的曲线上？并求出该曲线E的标准方程；

　　　 （2）过圆心F作直线交曲线E于A、B两点，若曲线E的

　　　　　　　　　中心为O，且， 求点A、B的坐标.

综合测试二

一、选择题：本题考查基本知识和基本运算，每小题5分，满分60分.

　　　 1．D　2．A　3．B　4．D　5．B　6．C　7．A　8．C　9．A　10． D

二、填空题：11．a≤－1，a＜－2等等　12．－2　13．60°　　14．4　　15．　　  16．2

三、解答题：

17． ∵　a²，

a²

　　　　　　　　　　　　　 

　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　

∴a²= 即a=．　　

　　　

18．（1）连A₁C交AC₁于E， 连ED，则ED为△A₁BC的中位线.∴ED∥A₁B.

（2）过D作DM⊥AC于M，作MN⊥AC₁于N，连ND，∠DNM即为二面角D—AC₁—C的平面角.

所求二面角的大小为arctan,π－arctan

19． （1）由

①当0<k<1时，得；

②当k=1时，得

　　　 ③当k>1时，得

综上所求函数的定义域：当0<k<1时为时为

 

（2）由上是增函数 得k>

又对任意的、，当时，

有得：

易求得k的取值范围是（）

20.答:命题推广为

　若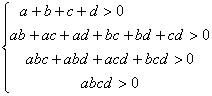　,则a、b、c、d、均为正.

　证明用反证法（略）

21．（1）∵F为定点，l为定直线，

　　　 ∴由椭圆第二定义可知，P点在以F为左焦点，l为左准线的椭圆上.

　　　 依题意知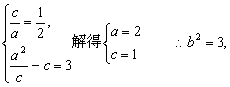

　　　 ∴曲线E的标准方程为.

　　　 （2）设

　　　

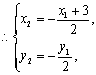　　又∵A、B都在椭圆上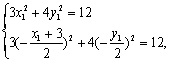，∴