上海市浦东新区2007年高考预测数学试卷(文史类)2007.4
(完卷时间:120分钟 满分:150分)
| 题 号 | 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | 总 分 |
| 得 分 |
一、填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.
1.设集合![]() ,则A∩B =___________________.
,则A∩B =___________________.
2.等差数列![]() 中,
中,![]() 4,
4,![]() ,则公差
,则公差![]() .
.
3.![]() =___________.
=___________.
4.向量![]() ,若
,若![]() ,则实数
,则实数![]() =_______.
=_______.
5.若圆![]() 关于直线
关于直线![]() 对称,则实数
对称,则实数![]() 的值为_______.
的值为_______.
6.![]() 中,
中,![]() 分别为角A,B,C的对边,若
分别为角A,B,C的对边,若![]() ,
,![]() ,
,![]() ,则边
,则边![]() .
.
7.某工程的工序流程如下表所示(工时数单位:天),则工程总时数为 天.
| 工序 | a | b | c | d | e | f |
| 紧前工序 | —— | a | a,b | c | c | d,e |
| 工时数(天) | 2 | 3 | 2 | 5 | 4 | 1 |
8.任取![]() 且
且![]() ,则点
,则点![]() 落在方程
落在方程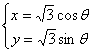 表示的曲线所围成的区域内的概率是____________.
表示的曲线所围成的区域内的概率是____________.
9.设变量![]() 满足约束条件
满足约束条件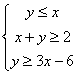 ,则目标函数
,则目标函数![]() 的最小值
的最小值![]() .
.
10.据有关资料统计,通过环境整治,某湖泊污染区域![]() 与时间
与时间![]() (年)可近似看作指
(年)可近似看作指
数函数关系,已知近2年污染区域由![]() 降至
降至![]() ,则污染区域降至
,则污染区域降至![]() 还
还
需要 年.
 11.如图,小正三角形沿着大正三角形的边,按逆时针方向无滑动地滚
11.如图,小正三角形沿着大正三角形的边,按逆时针方向无滑动地滚
动.小正三角形的边长是大正三角形边长的一半,如果小正三角形
沿着大正三角形的边滚动一周后返回出发时的位置,在这个过程中
向量![]() 围绕着点
围绕着点![]() 旋转了
旋转了![]() 角,其中
角,其中![]() 为小正三角形的中心,则
为小正三角形的中心,则
![]() .
.
12.对于函数![]() ,以下列四个命题中的两个为条件,余下
,以下列四个命题中的两个为条件,余下
的两个为结论,写出你认为正确的一个命题 .
①函数f (x)图像关于直线![]() 对称; ②函数f (x)在区间
对称; ②函数f (x)在区间![]() 上是增函数;
上是增函数;
③函数f (x)图像关于点![]() 对称; ④函数f (x)周期为
对称; ④函数f (x)周期为![]() .
.
二、选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结
论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的括号内,选对
得4分,不选、选错或者选出的代号超过一个(不论是否都写在括号内),一律得零分.
13.![]() ,“
,“![]() ”是“
”是“![]() ”的…………………………………………………( )
”的…………………………………………………( )
A.充分不必要条件 B.必要不充分条件
C.既充分也必要条件 D.既不必要也不充分条件
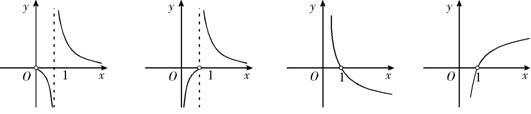 14.函数
14.函数![]() 的大致图象是………………………………………………( )
的大致图象是………………………………………………( )
A. B. C. D.
15.函数![]() 的值域为………………………………………………( )
的值域为………………………………………………( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
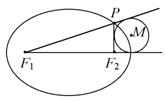 16.如图,已知点P在焦点为
16.如图,已知点P在焦点为![]() 的椭圆上运动,则
的椭圆上运动,则![]()
的边![]() 相切,且与边
相切,且与边![]() 的延长线相切的圆的圆心M
的延长线相切的圆的圆心M
一定在…………………………………………………( )
A.一条直线上 B.一个圆上
C.一个椭圆上 D.一条抛物线上
三、解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.
17.(本题满分12分)已知复数![]() ,若
,若![]() ,且
,且![]() ,求角
,求角![]() 的值.
的值.
[解]
18.(本题满分12分,第(1)题4分,第(2)题8分)
等差数列![]() 中,前
中,前![]() 项和为
项和为![]() ,首项
,首项![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)设![]() ,求使不等式b1
+ b2 + … + bn
> 30的最小正整数
,求使不等式b1
+ b2 + … + bn
> 30的最小正整数![]() 的值.
的值.
[解]
19.(本题满分14分,第(1)题6分,第(2)题8分)
据预测,某旅游景区游客人数在![]() 至
至![]() 人之间,游客人数
人之间,游客人数![]() (人)与游客的消费总额
(人)与游客的消费总额![]() (元)之间近似地满足关系:
(元)之间近似地满足关系:![]() .
.
(1)若该景区游客消费总额不低于![]() 元时,求景区游客人数的范围.
元时,求景区游客人数的范围.
(2)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额.
[解]
20.(本题满分14分,第(1)题7分,第(2)题7分)
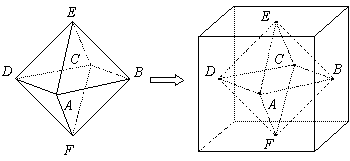
两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为![]() 的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
(1)若正子体的六个顶点分别是正方体各面的中心,求此正子体的体积;
(2)在(1)的条件下,求异面直线![]() 与
与![]() 所成的角.
所成的角.
 [解]
[解]
21.(本题满分16分,第(1)题4分,第(2)题7分,第(3)题5分)
记函数![]() ,
,![]() ,它们定义域的交集为
,它们定义域的交集为![]() ,若对任意的
,若对任意的![]() ,
,
![]() ,则称
,则称![]() 是集合
是集合![]() 的元素.
的元素.
(1)判断函数![]() 是否是
是否是![]() 的元素;
的元素;
(2)设函数![]() ,求
,求![]() 的反函数
的反函数![]() ,并判断
,并判断![]() 是否是
是否是![]() 的元素;
的元素;
(3)![]() (
(![]() ),求使
),求使![]() 成立的
成立的![]() 的范围.
的范围.
[解]
22.(本题满分18分.第(1)题4分,第(2)题6分,第(3)题8分)
已知直线l:y =![]() +b与抛物线y2 = 4x相交于A、B两点,︱AB︱= 8.
+b与抛物线y2 = 4x相交于A、B两点,︱AB︱= 8.
(1)求直线l的方程;
(2)求抛物线上横坐标为1的点D与点A、B构成的∆DAB的面积;
(3)设P(x, y)是抛物线上的动点,试用x或y来讨论∆PAB面积![]() 的取值范围.
的取值范围.
[解]
上海市浦东新区2007年高考预测
数学试卷(文史类)参考答案与评分标准(文科) 2007/4
一、填空题
1.![]() 2.1 3.
2.1 3.![]() 4.
4.![]() 5.2 6.5 7.13
5.2 6.5 7.13
8.![]() 9.3 10.2 11.
9.3 10.2 11.![]() 12.③④
12.③④![]() ①②或①④
①②或①④![]() ②③
②③
二、选择题
13.B 14.A 15.D 16.A
三、解答题
17.解:由![]() 得:
得:![]() ,所以
,所以![]() ,
,![]() --------------4分
--------------4分
![]() ,
,![]() ------------------------------------------5分
------------------------------------------5分
![]() ---------------------------------------------7分
---------------------------------------------7分
![]() ,
,![]() ----------------8分
----------------8分
![]() ------------------10分
------------------10分 ![]() 或
或![]() ------------------------12分
------------------------12分
18.解:(1)![]() ,得:
,得:![]() ,
,![]() -------------------------3分
-------------------------3分
由![]() ,
,![]()
![]() ,得到
,得到![]() ---------------------------------------------6分
---------------------------------------------6分
(2)![]() ,
,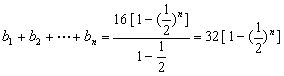 ,------9分
,------9分
![]() ,得
,得![]() ,所以正整数
,所以正整数![]() 的最小值为
的最小值为![]() 。---------------12分
。---------------12分
19.解:(1)![]()
![]() ,得
,得![]() -------------------------------------4分
-------------------------------------4分
又![]() ,所以景区游客人数的范围是1000至1300人-------------6分
,所以景区游客人数的范围是1000至1300人-------------6分
(2)设游客的人均消费额为![]() ,则
,则
![]() ---------------------12分
---------------------12分
当且仅当![]() 时等号成立。---------------------------------------------------------14分
时等号成立。---------------------------------------------------------14分
答:当景区游客的人数为![]() 时,游客的人均消费最高,最高消费额为
时,游客的人均消费最高,最高消费额为![]() 元。
元。
 20.解:(1)因为正子体的各个顶点是正方体
20.解:(1)因为正子体的各个顶点是正方体
各面的中心,所以![]()
![]() -------------------------------------2分
-------------------------------------2分
正四棱锥![]() 的底面积
的底面积![]() ,高
,高![]() ---------------------------------5分
---------------------------------5分
正子体体积![]() ---------------------------------------------7分
---------------------------------------------7分
(2)方法一:建立空间直角坐标系,评分标准见理科答案。
方法二:记正方体为![]() ,
,
记棱![]() 中点为
中点为![]() ,
,![]() 中点为
中点为![]() ----------------------------------------------------------8分
----------------------------------------------------------8分
则![]() ,所以
,所以![]() -------------------------------------------------10分
-------------------------------------------------10分
异面直线![]() 与
与![]() 所成的角即为
所成的角即为![]() ------------------------------------------------11分
------------------------------------------------11分
又因为![]() ,故
,故![]() =
=![]() ------------------------------------14分
------------------------------------14分
异面直线![]() 与
与![]() 所成的角为
所成的角为![]() 。
。
21.解:(1)∵对任意![]() ,
,![]() ,∴
,∴![]() --2分
--2分
∵![]() 不恒等于
不恒等于![]() ,∴
,∴![]() --------------------------4分
--------------------------4分
(2)设![]()
由![]() 解得:
解得:![]() ----------------------------------------------------6分
----------------------------------------------------6分
由![]()
![]() ,反函数为
,反函数为 ![]() ,
,![]() -------8分
-------8分
∵![]()
∴![]() --------------------------------------------------------------------11分
--------------------------------------------------------------------11分
(3)∵![]() ,∴
,∴![]() 对一切定义域中
对一切定义域中![]() 恒成立。
恒成立。
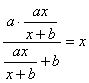 ,解得:
,解得:![]() 恒成立,故
恒成立,故![]() ----------13分
----------13分
由![]() ,得到
,得到![]() ,
,![]() ,由
,由![]() ,
,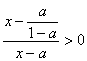 --14分
--14分
![]() -------------15分,故
-------------15分,故![]() 的范围为:
的范围为:![]() 或
或 ![]() -------------16分
-------------16分
22.解:(1)把![]() 代入
代入![]() 得
得![]() 。
。
令![]() ,得
,得![]() 。
---------------------------------------------------------------------------2分
。
---------------------------------------------------------------------------2分
设![]() ,则
,则![]() -------------------------------4分
-------------------------------4分
∴![]() , ∴直线的方程为y= -x+1。 ------------------------------------6分
, ∴直线的方程为y= -x+1。 ------------------------------------6分
(2)设D (1 , y0),代入y 2= 4x,得![]() 因此得到D点坐标:D (1,2 ) 或D′(1,-2)
因此得到D点坐标:D (1,2 ) 或D′(1,-2)
点D(D′)到直线y=-x+1的距离![]() . ----------------------------------------8分
. ----------------------------------------8分
∴∆DAB的面积为![]() 。------------------------------------------------------------------------10分
。------------------------------------------------------------------------10分
(3)设与直线y=-x+1平行且与y2 = 4 x相切的直线为y=-x+t, 代入y 2 =4 x,
得![]() ,令∆=0,得
,令∆=0,得![]() ,此时切点为
,此时切点为![]() 。
。
另解:设与直线![]() 平行且距离为
平行且距离为![]() 的直线为y=-x+t, 得
的直线为y=-x+t, 得![]() 或3------12分
或3------12分
![]() 与 y 2 =
4 x的交点仅有一个为
与 y 2 =
4 x的交点仅有一个为 ![]() ,
,
y = - x +3与y 2 = 4 x的交点为 ![]() ,
,![]() 。
。
y=-x+1与y2=4x的交点为![]()
∴当![]() 时,
时,![]() ---------------------------------------------------------14分
---------------------------------------------------------14分
当![]() 时,
时,
![]() --------------------------------------------------------------------------------------16分
--------------------------------------------------------------------------------------16分
当![]() 时,
时,![]() 。-------------------------------------18分
。-------------------------------------18分