上海市浦东新区2007年高考预测数学试卷(理工类)2007.4
(完卷时间120分钟 满分150分)
| 题 号 | 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | 总 分 |
| 得 分 |
一、填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.
1.设集合![]() ,则A∩B =___________________.
,则A∩B =___________________.
2.![]() =_________________.
=_________________.
3.已知向量![]() 平行,则实数
平行,则实数![]() =_________________.
=_________________.
4.在二项式![]() 的展开式中,含
的展开式中,含![]() 项的系数为
.
项的系数为
.
5.已知圆![]() 关于直线
关于直线![]() 对称,则实数
对称,则实数![]() 的值为________.
的值为________.
6.![]() 中,
中,![]() 分别为角A,B,C的对边,若
分别为角A,B,C的对边,若![]() ,
,![]() ,
,![]() ,则边
,则边![]() .
.
7.在极坐标系中,点![]() ,则
,则![]() 中点的极坐标为
.
中点的极坐标为
.
8.任取![]() 且
且![]() ,则点
,则点![]() 落在方程
落在方程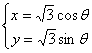 表示的曲
表示的曲
线所围成的区域内的概率是____________.
9.据有关资料统计,通过环境整治,某湖泊污染区域![]() 与时间
与时间![]() (年)可近似看作指
(年)可近似看作指
数函数关系,已知近2年污染区域由![]() 降至
降至![]() ,则污染区域降至
,则污染区域降至![]() 还
还
 需要 年.
需要 年.
10.如图,小正三角形沿着大正三角形的边,按逆时针方向无滑动地滚
动.小正三角形的边长是大正三角形边长的一半,如果小正三角形沿
着大正三角形的边滚动一周后返回出发时的位置,在这个过程中向量
![]() 围绕着点
围绕着点![]() 旋转了
旋转了![]() 角,其中
角,其中![]() 为小正三角形的中心,则
为小正三角形的中心,则
![]() .
.
11.对于函数![]() ,以下列四个命题中的两个为条件,余下
,以下列四个命题中的两个为条件,余下
的两个为结论,写出你认为正确的一个命题 .
①函数f (x)图像关于直线![]() 对称; ②函数f (x)在区间
对称; ②函数f (x)在区间![]() 上是增函数;
上是增函数;
③函数f (x)图像关于点![]() 对称; ④函数f (x)周期为
对称; ④函数f (x)周期为![]() .
.
|
![]()
 和,求证:它的对角线互相垂直.下面利用向量方法进行证明:
和,求证:它的对角线互相垂直.下面利用向量方法进行证明:
|
|
![]() 则
则![]()
|
反思上面的证明过程,对该命题进行推广,写出你的结论:
二、选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、C、D的四个结
论,其中有且只有一个结论是正确的,必须把正确结论的代号写在题后的括号内,选对
得4分,不选、选错或者选出的代号超过一个(不论是否都写在括号内),一律得零分.
13.![]() ,“
,“![]() ”是“
”是“![]() ”的 …………………………………………………( )
”的 …………………………………………………( )
A.充分不必要条件 B.必要不充分条件
C.既充分也必要条件 D.既不必要也不充分条件
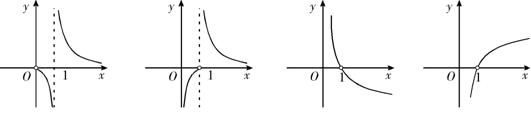 14.函数
14.函数![]() 的大致图象是 ………………………………………………( )
的大致图象是 ………………………………………………( )
A. B. C. D.
15.设![]() 是非空集合,且
是非空集合,且![]() ,定义在
,定义在![]() 上的函数
上的函数![]() 的值域为…( )
的值域为…( )
A.![]() B.
B.![]() C.
C.![]() D.以上都不对
D.以上都不对
16.如图,已知点P在焦点为![]() 的椭圆上运动,则与
的椭圆上运动,则与![]()
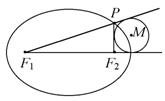 的边
的边![]() 相切,且与边
相切,且与边![]() 的延长线相切的圆的圆心M
的延长线相切的圆的圆心M
一定在 …………………………………………………( )
A.一条直线上 B.一个圆上
C.一个椭圆上 D.一条抛物线上
三、解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要的步骤.
17.(本题满分12分)
已知复数![]() ,若
,若![]() ,且
,且![]() ,求角
,求角![]() 的值.
的值.
[解]
18.(本题满分12分,第(1)题5分,第(2)题7分)
据预测,某旅游景区游客人数在![]() 至
至![]() 人之间,游客人数
人之间,游客人数![]() (人)与游客的消费总额
(人)与游客的消费总额![]() (元)之间近似地满足关系式:
(元)之间近似地满足关系式:![]() .
.
(1)若该景区游客消费总额不低于![]() 元时,求景区游客人数的范围.
元时,求景区游客人数的范围.
(2)当景区游客的人数为多少人时,游客的人均消费最高?并求游客的人均最高消费额.
[解]
19.(本题满分14分,第(1)题6分,第(2)题8分)
等差数列![]() 中,前
中,前![]() 项和为
项和为![]() ,首项
,首项![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)设![]() ,求使不等式b1 + b2 + … + bn >
2007的最小正整数
,求使不等式b1 + b2 + … + bn >
2007的最小正整数![]() 的值.
的值.
[解]
20.(本题满分14分,第(1)题7分,第(2)题7分)
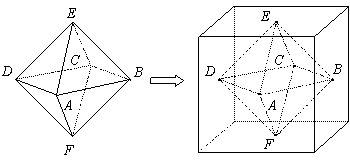
两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为![]() 的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.
(1)若正子体的六个顶点分别是正方体各面的中心,求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)问此正子体的体积V是否为定值?若是,求出该定值;若不是,求出体积大小的取值范围.
[解]
21.(本题满分16分,第(1)题4分,第(2)题7分,第(3)题5分)
记函数![]() ,
,![]() ,它们定义域的交集为
,它们定义域的交集为![]() ,若对任意的
,若对任意的
![]() ,
,![]() ,则称
,则称![]() 是集合
是集合![]() 的元素.
的元素.
(1)判断函数![]() 是否是
是否是![]() 的元素;
的元素;
(2)设函数![]() ,求
,求![]() 的反函数
的反函数![]() ,并判断
,并判断![]() 是否是
是否是![]() 的元素;
的元素;
(3)若![]() ,写出
,写出![]() 的条件,并写出两个不同于(1)、(2)中的函数.(将根据写出的函数类型酌情给分)
的条件,并写出两个不同于(1)、(2)中的函数.(将根据写出的函数类型酌情给分)
[解]
22.(本题满分18分.第(1)题4分,第(2)题14分,分别为4、4、6分)
已知抛物线![]() 上横坐标为
上横坐标为![]() 的点到焦点的距离为
的点到焦点的距离为![]() .
.
(1)求抛物线![]() 的方程.
的方程.
(2)设直线![]() 与抛物线
与抛物线![]() 交于两点
交于两点![]() ,且
,且
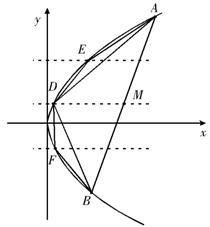
![]() ,
,![]() 是弦
是弦![]() 的中点,过
的中点,过![]() 作平行于
作平行于![]() 轴的直线交抛物线
轴的直线交抛物线![]() 于点
于点![]() ,得到
,得到![]() ;再分别过弦
;再分别过弦![]() 、
、![]() 的中点作平行于
的中点作平行于![]() 轴的直线依次交抛物线
轴的直线依次交抛物线![]() 于点
于点![]() ,得到
,得到![]() 和
和![]() ;按此方法继续下去.
;按此方法继续下去.
解决下列问题:
1 求证:![]() ;
;
2 计算![]() 的面积
的面积![]() ;
;
3 根据![]() 的面积
的面积![]() 的计算结果,写出
的计算结果,写出![]()
的面积;请设计一种求抛物线![]() 与线段
与线段![]() 所围成封闭图
所围成封闭图
形面积的方法,并求出此封闭图形的面积.
[解]
上海市浦东新区2007年高考预测
数学试卷(文史类)参考答案与评分标准(理科) 2007/4
一、填空题
1.![]() 2.
2.![]() 3.
3.![]() 4.80 5.4 6.5 7.
4.80 5.4 6.5 7.![]()
8.![]() 9.2
10.
9.2
10.![]() 11.③④
11.③④![]() ①②或①④
①②或①④![]() ②③
②③
12.已知空间四边形一组对边的平方和等于另一组对边的平方和,则空间四边形余下的一组对边(对角线)互相垂直.
二、选择题
13.B 14.A 15.D 16.A
三、解答题
17.解:由![]() 得:
得:![]() ,所以
,所以![]() ,
,![]() ---------------4分
---------------4分
![]() ,
,![]() -------------------------------------------5分
-------------------------------------------5分
![]() ----------------------------------------------7分
----------------------------------------------7分
![]() ,
,![]() --------------8分
--------------8分
![]() ------------------10分
------------------10分 ![]() 或
或![]() --------------------12分
--------------------12分
18.解:(1)由已知:![]() ,即
,即
![]() ,解得
,解得![]() ---------------------------------4分
---------------------------------4分
又![]() ,所以景区游客人数的范围是1000至1300人 -------------5分
,所以景区游客人数的范围是1000至1300人 -------------5分
(2)设游客的人均消费额为![]() ,则
,则
![]() ----------------------9分
----------------------9分
当且仅当![]() 时等号成立.
----------------------------------------------------12分
时等号成立.
----------------------------------------------------12分
答:当景区游客的人数为![]() 时,游客的人均消费最高,最高消费额为
时,游客的人均消费最高,最高消费额为![]() 元.
元.
19.解:(1)![]() ,得:
,得:![]() ,
,![]() -----------------------------2分
-----------------------------2分
由![]() ,
,![]()
![]() ,得到
,得到![]() -------------------------------------------------6分
-------------------------------------------------6分
(2)![]() ,
,
若![]() ,则
,则![]() ,不合题意-----------------9分
,不合题意-----------------9分
故![]() ,
,![]() -------------------------------11分
-------------------------------11分
![]() ,所以
,所以![]() ,使不等式成立的最小正整数
,使不等式成立的最小正整数![]() 的值为15.-----------14分
的值为15.-----------14分
20.解:(1)方法一:如图,分别以CA、DB为![]() 、
、![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
因为![]() ,所以
,所以![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ---------------4分
---------------4分 ![]() -----------------6分
-----------------6分
因为异面直线所成角为锐角,故异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ----------------7分
----------------7分
方法二:见文科答案与评分标准.
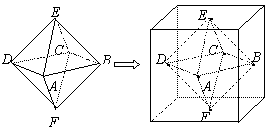 (2)正子体体积不是定值.-------------8分
(2)正子体体积不是定值.-------------8分
设![]() 与正方体的截面四边形为
与正方体的截面四边形为
![]() , 设
, 设![]()
![]()
则![]() ----------------------------9分
----------------------------9分
![]()
故![]() ----------------------------------------------------------------------12分
----------------------------------------------------------------------12分
![]() -----------------------------14分
-----------------------------14分
21.解:(1)∵对任意![]() ,
,![]() ,∴
,∴![]() --2分
--2分
∵![]() 不恒等于
不恒等于![]() ,∴
,∴![]() --------------------------4分
--------------------------4分
(2)设![]()
①![]() 时,由
时,由![]() 解得:
解得:![]()
由![]() 解得其反函数为
解得其反函数为 ![]() ,
,![]() -----------------6分
-----------------6分
②![]() 时,由
时,由![]() 解得:
解得:![]()
解得函数![]() 的反函数为
的反函数为![]() ,
,![]() --------------------8分
--------------------8分
∵![]()
∴![]() --------------------------------------------------------------------11分
--------------------------------------------------------------------11分
(3)![]() ,
,![]() 的条件是:
的条件是:
![]() 存在反函数
存在反函数![]() ,且
,且![]() -----------------------------------------------13分
-----------------------------------------------13分
函数![]() 可以是:
可以是:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() 或
或![]() ,
,![]() ;
;
![]() 或
或![]() ,
,![]() .
.
以“;”划分为不同类型的函数,评分标准如下:
给出函数是以上函数中两个不同类型的函数得3分.
属于以上同一类型的两个函数得1分;
写出的是与(1)、(2)中函数同类型的不得分;
函数定义域或条件错误扣1分.
22.解:(1)由抛物线定义,抛物线![]() 上点
上点![]() 到焦点的距离等于它到准线
到焦点的距离等于它到准线![]() 的距离,得
的距离,得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() . ----------------------------------------------------------4分
. ----------------------------------------------------------4分
(只要得到抛物线方程,都得4分)
(2)由![]() ,得
,得![]() ,(或
,(或![]() )
)
当![]() ,即
,即![]() 且
且![]() 时,
时,
![]() (或
(或![]() )
)
①由![]() ,即
,即![]() ,得
,得![]() ,
,
所以![]() .----------------------------------------------------------------------8分
.----------------------------------------------------------------------8分
②由①知,![]() 中点
中点![]() 的坐标为
的坐标为![]() ,点
,点![]() ,
,
![]()
![]() .-------------------------------------12分
.-------------------------------------12分
③由问题②知,![]() 的面积值仅与
的面积值仅与![]() 有关,由于
有关,由于
![]() ,所以
,所以![]() 与
与![]() 的面积
的面积
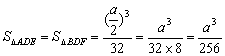 ,设
,设![]() -------14分
-------14分
由题设当中构造三角形的方法,可以将抛物线![]() 与线段
与线段![]() 所围成的封闭图形的面积
所围成的封闭图形的面积
看成无穷多个三角形的面积的和,即数列![]() 的无穷项和,------------------------16分
的无穷项和,------------------------16分
所以![]()
即![]() ,
,
因此,所求封闭图形的面积为![]() .--------------------------------------------------------18分
.--------------------------------------------------------18分