高考数学二轮复习一元二次函数性质及其综合考查
一、一元二次函数图象与性质：（学生画出函数图象，写出函数性质）
二.高考题热身
1.若不等式x2＋ax＋1³0对于一切xÎ（0，
〕成立，则a的取值范围是（ ）
A．0
B. –2
C.-
D.-3
2.已知函数f(x)=ax2+2ax+4(a>0),若x1<x2 , x1+x2=0 , 则( )
A.f(x1)<f(x2) B.f(x1)=f(x2) C.f(x1)>f(x2) D.f(x1)与f(x2)的大小不能确定
3．过点（－1，0）作抛物线
的切线，则其中一条切线为
（A）
（B）
（C）
（D）
3.设
，
，曲线
在点
处切线的倾斜角的取值范围为
，则点Ｐ到曲线对称轴距离的取值范围是（ ）
B.
4．设
，二次函数
的图像为下列之一（ ）
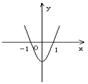
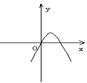
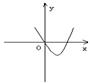
则
的值为
（A）
（B）
（C）
（D）
5.不等式组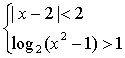
的解集为 ( )
(A) (0,
)； (B) (,2)； (C) (,4)； (D) (2,4)。
6．一元二次方程
有一个正根和一个负根的充分不必要条件是：（ ）
A．
B． C．
D．
7. 已知方程
的四个根组成一个首项为
的等差数列,则
(
)
A 1 B 
C 
D 
8.已知
( )
A.
B.
C. 
D.
9. 设函数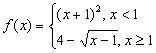
，则使得
的自变量
的取值范围为 （ ）
A．
B．
C．
D．
9.函数
在区间［1，2］上存在反函数的充分必要条件是（ ）
A. 
B. 
C. 
D. 
10.已知函数
的解析式可能为 （ ）
A．
B．
C．
D．
11. 定义在R上的偶函数f(x)满足f(x)=f(x+2)，当x∈[3，5]时，f(x)=2－x－4，则（ ）
A．f(sin
)<f(cos)
B．f(sin1)>f(cos1)
C．f(cos
)<f(sin)
D．f(cos2)>f(sin2)
12．命题p：若a、b∈R，则a+b>1是a+b>1的充分而不必要条件；
命题q：函数y=
的定义域是（－∞，－1
∪[3，+∞
.则（ ）
A．“p或q”为假 B．“p且q”为真 C．p真q假 D．p假q真
13. .已知关于的方程
－(2 m－8)x +
－16 = 0的两个实根 
满足 
＜
＜
，则实数m的取值范围_______________.
14.已知
为常数，若
，
，则
= 2 。
15.设函数f(x)=x2+mx+n,
若不等式
的解集为{x2≤x≤3或x=6},求m,n的值.
三.典型例题
例1．作出下列函数的图象(1)y=x-2(x＋1)；
解：(1)当x≥2时，即x-2≥0时，
当x＜2时，即x-2＜0时，
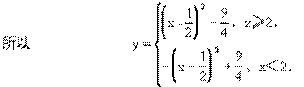
这是分段函数，每段函数图象可根据二次函数图象作出(见图6)
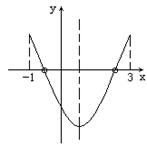
例2.
解析：
，
例3．（福建卷）已知
是二次函数，不等式
的解集是
且在区间
上的最大值是12。 （I）求的解析式； （II）是否存在实数
使得方程
在区间
内有且只有两个不等的实数根？若存在，求出
的取值范围；若不存在，说明理由。
解：（I）
是二次函数，且
的解集是
可设
在区间
上的最大值是
由已知，得
（II）方程
等价于方程
设
则
当
时，
是减函数；当
时，
是增函数。 
方程
在区间
内分别有惟一实数根，而在区间
内没有实数根，所以存在惟一的自然数
使得方程
在区间内有且只有两个不同的实数根。
例4：已知二次函数f(x)=ax2+bx+c和一次函数g(x)=－bx，其中a、b、c满足a>b>c,a+b+c=0,(a,b,c∈R)
(1)求证
两函数的图象交于不同的两点A、B； (2)求线段AB在x轴上的射影A1B1的长的取值范围
解: (1)证明由
消去y得ax2+2bx+c=0
Δ=4b2－4ac=4(－a－c)2－4ac=4(a2+ac+c2)=4［(a+
c2］
∵a+b+c=0,a>b>c,∴a>0,c<0 ∴
c2>0,∴Δ>0,即两函数的图象交于不同的两点
(2)解设方程ax2+bx+c=0的两根为x1和x2,则x1+x2=－
,x1x2=
A1B12=(x1－x2)2=(x1+x2)2－4x1x2
∵a>b>c,a+b+c=0,a>0,c<0，∴a>－a－c>c,解得
∈(－2,－
)
∵
的对称轴方程是
∈(－2,－
)时，为减函数
∴A1B12∈(3,12),故A1B1∈(
)
例5：已知f(x)=x2+c,且f［f(x)］=f(x2+1) (1)设g(x)=f［f(x)］,求g(x)的解析式；(2)设φ(x)=g(x)－λf(x),试问 是否存在实数λ,使φ(x)在(－∞,－1)内为减函数，且在(－1，0)内是增函数
点拨与提示：由f［f(x)］=f(x2+1)求出c，进而得到函数的解析式，利用导数研究函数的单调性.
解: (1)由题意得f［f(x)］=f(x2+c)=(x2+c)2+c, f(x2+1)=(x2+1)2+c,∵f［f(x)］=f(x2+1)
∴(x2+c)2+c=(x2+1)2+c,∴x2+c=x2+1,∴c=1 ∴f(x)=x2+1,g(x)=f［f(x)］=f(x2+1)=(x2+1)2+1
(2)φ(x)=g(x)－λf(x)=x4+(2－λ)x2+(2－λ)
若满足条件的λ存在，则φ′(x)=4x3+2(2－λ)x
∵函数φ(x)在(－∞,－1)上是减函数， ∴当x＜－1时，φ′(x)＜0
即4x3+2(2－λ)x＜0对于x∈(－∞,－1)恒成立
∴2(2－λ)＞－4x2, ∵x＜－1,∴－4x2＜－4 ∴2(2－λ)≥－4,解得λ≤4
又函数φ(x)在(－1,0)上是增函数 ∴当－1＜x＜0时，φ′(x)＞0
即4x2+2(2－λ)x＞0对于x∈(－1,0)恒成立
∴2(2－λ)＜－4x2, ∵－1＜x＜0,∴－4＜4x2＜0 ∴2(2－λ)≤－4,解得λ≥4
故当λ=4时，φ(x)在(－∞,－1)上是减函数，在(－1,0)上是增函数，即满足条件的λ存在
例6. 已知
，t∈[
，8]，对于f(t)值域内的所有实数m，不等式
恒成立，求x的取值范围。
解:∵t∈[
，8]，∴f(t)∈[，3]原题转化为：
>0恒成立，为m的一次函数（这里思维的转化很重要）当x＝2时，不等式不成立。∴x≠2。令g(m)＝，m∈[，3]问题转化为g(m)在m∈[，3]上恒对于0，则：
；解得：x>2或x<－1
例8.
(见备考指南148页例3)
解：
综上所述，得原不等式的解集为
；
；
；
；
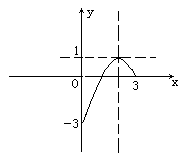
例9. 若方程
上有唯一解，
求m的取值范围。
解：原方程等价于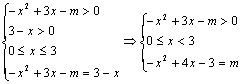
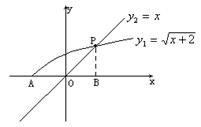
令
，在同一坐标系内，画出它们的图象，
其中注意
，当且仅当两函数的图象在[0，3）上有唯一公共点时，原方程有唯一解，由下图可见，当m=1，或
时，原方程有唯一解，因此m的取值范围为[－3，0]
{1}。
例10．设函数f(x)=ax2+bx+c的图象与两直线y=x，y=
x，均不相交.试证明对一切
都有
.
证明：由题意知，a≠0．设f(x)=a(x-x0)2+f(x0)，则
又二次方程ax2+bx+c=±x无实根，故 Δ1=(b+1)2-4ac＜0，Δ2=(b-1)2-4ac＜0．
所以(b+1)2+(b-1)2-8ac＜0，即2b2+2-8ac＜0，即b2-4ac＜-1，所以b2-4ac＞1．
