北京市朝阳区2006~2007学年度高三年级第二次统一考试
数学试卷(文科) 2007.5
(考试时间120分钟, 满分150分)
第Ⅰ卷 (选择题共40分)
| 得分 | 评卷人 |
一、选择题:本大题共8小题,每小题5分,共40分. 在每小题的
4个选项中,只有一项是符合题目要求的.
(1)不等式![]() >0的解集是
( )
>0的解集是
( )
A. {x x >5或 x<2} B. {x 2< x<5}
C. {x x >5或 x<-2} D. {x -2< x<5}
(2)与函数y=2x的图象关于y轴对称的函数图象是 ( )
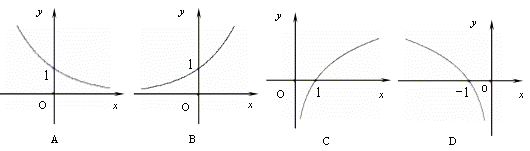
(3)已知直线a 、b和平面![]() 、
、![]() ,
,![]() ∩
∩![]() =l,a
=l,a![]()
![]() ,b
,b![]()
![]() ,则a 、b的位置关系可能是
( )
,则a 、b的位置关系可能是
( )
A.相交或平行 B.相交或异面 C.平行或异面 D.相交、平行或异面
(4)把函数![]() 的图象向右平移
的图象向右平移![]() 个单位,所得的图象对应的函数是 ( )
个单位,所得的图象对应的函数是 ( )
A.奇函数 B.偶函数 C.既是奇函数又是偶函数 D.非奇非偶函数
(5)二项式(x-![]() )9的展开式中含x5的项的系数是
( )
)9的展开式中含x5的项的系数是
( )
A.72 B.-72 C.36 D.-36
(6) 某电视台连续播放5个广告,其中3个不同的商业广告和2个不同的奥运宣传广告,要求最后播放的必须是奥运宣传广告,且2个奥运宣传广告不能连续播放,则不同的播放方式有 ( )
A.120种 B.48种 C.36种 D.18种
(7) 设f(x)=x2+bx+c且f(0)= f(2),则 ( )
A.f(-2)< c< f(![]() ) B.f(
) B.f(![]() )< c< f(-2)
)< c< f(-2)
C.f(![]() )<f(-2) <c D. c< f(
)<f(-2) <c D. c< f(![]() )<f(-2)
)<f(-2)
(8) 已知圆F的方程是![]() ,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为
,抛物线的顶点在原点,焦点是圆心F,过F引倾斜角为![]() 的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若
的直线l,l与抛物线和圆依次交于A、B、C、D四点(在直线l上,这四个点从左至右依次为A、B、C、D),若![]() ,
,![]() ,
,![]() 成等差数列,则
成等差数列,则![]() 的值为 ( )
的值为 ( )
A.±arctan![]() B.
B.![]()
C.arctan![]() D.arctan
D.arctan![]() 或π- arctan
或π- arctan![]()
朝阳区高三第二次统一考试数学试卷(文科)
第II卷(非选择题 共110分)
| 二 题 | 9 | 10 | 11 | 12 | 13 | 14 | 二题 总分 | |||||||||||||||
| 三 题 | 15 | 16 | 17 | 18 | 19 | 20 | ||||||||||||||||
| Ⅰ | Ⅱ | Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅰ | Ⅱ | Ⅰ | Ⅱ | Ⅲ | ||||||||
| 三题 总分 | 二卷 总分 | |||||||||||||||||||||
| 得分 | 评卷人 |
二、填空题:本大题共6小题,每小题5分,共30分.将答案填在题中
横线上.
(9) 已知向量a= (4,3),b = (x,-4),且a⊥b,则x = .
(10)由正数组成的等比数列{an}中,a1=![]() ,a2·a4=9,则a5= ,
,a2·a4=9,则a5= ,![]() = .
= .
(11) 若x,y满足约束条件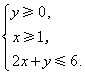 则z=x+y的最大值为 .
则z=x+y的最大值为 .
(12) 已知曲线C的参数方程是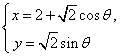 (θ为参数),则曲线C的普通方
(θ为参数),则曲线C的普通方
 程是
;曲线C被直线
程是
;曲线C被直线
x-![]() y=0所截得的弦长是 .
y=0所截得的弦长是 .
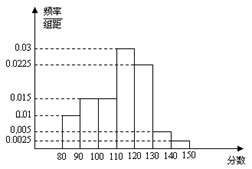
(13) 高三某班50名学生参加某次数学模
拟考试 所得的成绩(成绩均为整数)整理后
画出的频率分布直方图如右图,则该班得
120分以上的同学共有 人.
(14) 在△ABC中,E、F分别为AB、AC上的点,若![]() =m,
=m,![]() =n,
=n,
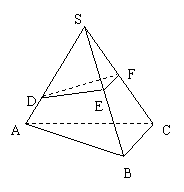 则
则![]() = mn.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若
= mn.拓展到空间:在三棱锥S-ABC中,D、E、F分别是侧棱SA、SB、SC上的点,若![]() = m,
= m,![]() =
=![]() = n,则
= n,则![]() =
.
=
.
 |
三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤.
| 得分 | 评卷人 |
(15) (本小题满分13分)
△ABC中,角A、B、C的对边分别为a,b,c,且![]() .
.
(Ⅰ)求cosA的值;
(Ⅱ)求![]() 的值.
的值.
| 得分 | 评卷人 |
(16)(本小题满分13分)
一个袋子里装有大小相同且标有数字1~5的若干个小球,其中标有数字1的小球有1个,标有数字2的小球有2个,…,标有数字5的小球有5个.
(Ⅰ) 从中任意取出1个小球, 求取出的小球标有数字3的概率;
(Ⅱ) 从中任意取出3个小球,求其中至少有1个小球标有奇数数字的概率;
(Ⅲ) 从中任意取出2个小球,求小球上所标数字之和为6的概率.
| 得分 | 评卷人 |
(17) (本小题满分13分)
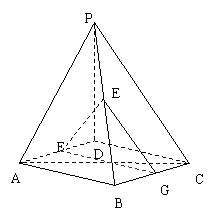
 已知:四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=1.
已知:四棱锥P-ABCD的底面ABCD是边长为1的正方形,PD⊥底面ABCD,且PD=1.
(Ⅰ) 求证:BC∥平面PAD;
(Ⅱ) 若E、F分别为PB、AD的中点,求证:EF⊥BC;
(Ⅲ) 求二面角C-PA-D的余弦值.
| 得分 | 评卷人 |
(18)(本小题满分13分)
已知函数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(Ⅱ) 若函数![]() 的图象上存在点P,使P点处的切线与x轴平行,求实数a,b所满足的关系式.
的图象上存在点P,使P点处的切线与x轴平行,求实数a,b所满足的关系式.
| 得分 | 评卷人 |
(19)(本小题满分14分)
已知O为坐标原点,点E、F的坐标分别为(-1,0)、(1,0),动点A满足![]() ,N为AF的中点,点M在线段AE上,
,N为AF的中点,点M在线段AE上,![]() .
.
(Ⅰ)求点M的轨迹W的方程;
(Ⅱ)点![]() 在轨迹W上,直线PF交轨迹W于点Q,且
在轨迹W上,直线PF交轨迹W于点Q,且![]() ,若
,若![]() ,求实数
,求实数![]() 的范围.
的范围.
| 得分 | 评卷人 |
(20)(本小题满分14分)
在下列由正数排成的数表中,每行上的数从左到右都成等比数列,并且所有公比都等于![]() ,每列上的数从上到下都成等差数列.
,每列上的数从上到下都成等差数列.![]() 表示位于第
表示位于第![]() 行第
行第![]() 列的数,其中
列的数,其中![]() ,
,![]() ,
,![]() .
.
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
|
|
|
|
|
| … |
| … |
| … | … | … | … | … | … | … | … |
(Ⅰ) 求![]() 的值;
的值;
(Ⅱ) 求![]() 的计算公式;
的计算公式;
(Ⅲ)设数列{bn}满足bn=ann,{bn}的前![]() 项和为
项和为![]() ,求
,求![]() .
.
朝阳区高三第二次统一考试
数学试卷答案(文科) 2007.5
一.选择题
(1)B (2)A (3)D (4)B (5)C (6) C (7) B (8)D
二.填空题
(9)3 (10)27 ,![]() (11)5
(12)( x-2)2+ y2=2,2
(11)5
(12)( x-2)2+ y2=2,2
(13)15 (14)mn2
三.解答题
(15) 解:(Ⅰ)∵![]() ,
,
∴![]() . ……………………………………………………3分
. ……………………………………………………3分
∴![]() .
…………………………………………………………5分
.
…………………………………………………………5分
(Ⅱ)∵![]()
![]()
=2cos2A+![]() cosA-
cosA-![]() , ………………………………………………9分
, ………………………………………………9分
由(Ⅰ)知![]() ,代入上式得
,代入上式得
![]() =2(
=2(![]() )2+
)2+![]() ×
×![]() -
-![]() = -
= -![]() . …………………………………13分
. …………………………………13分
(16) 解: 袋子里共装有1+2+3+4+5=15个小球.
(Ⅰ) ∵ 标有数字3的小球共有3个,
∴ 取出标有数字3的小球的概率为 ![]() . ……………………4分
. ……………………4分
(Ⅱ) 标有偶数数字的小球共有2+4=6个,
取出的3个小球全标有偶数数字的概率为![]() ………………………………6分
………………………………6分
∴任意取出3个小球中至少有1个标有奇数数字的概率为
![]() …………………………………8分
…………………………………8分
(Ⅲ) 2个小球上所标数字之和为6有三种情况,即(1,5),(2,4),(3,3). …10分
所求概率 ![]() ………………………13分
………………………13分
(17) 方法1:
(Ⅰ)解:因为ABCD是正方形,
所以BC∥AD.
因为AD![]() 平面PAD,BC
平面PAD,BC![]() 平面PAD,
平面PAD,
所以BC∥平面PAD. ………………4分
 (Ⅱ)证明:因为PD⊥底面ABCD,
(Ⅱ)证明:因为PD⊥底面ABCD,
且ABCD是正方形,
所以PC⊥BC.
设BC的中点为G,
连结EG,FG,则EG∥PC,FG∥DC.
所以BC⊥EG,BC⊥FG. …………………6分
因为 EG∩FG=G,
所以BC⊥面EFG.
因为EF![]() 面EFG,
面EFG,
所以EF⊥BC. …………………………8分
(Ⅲ)设PA的中点为N,连结DN,NC,
因为PD=AD,N为中点,
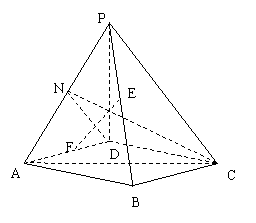 所以DN⊥PA.
所以DN⊥PA.
又△PAC中容易计算出PC=AC,
N为中点,所以NC⊥PA.
所以∠CND是所求二面角的平面角. ………10分
依条件,有CD⊥PD,CD⊥AD,
PD∩AD=D,
所以CD⊥面PAD.
因为DN![]() 面PAD,
面PAD,
所以CD⊥DN.
在Rt△CND中,容易计算出DN=![]() ,NC=
,NC=![]() .
.
 于是cos∠CND=
于是cos∠CND=![]() =
=![]() ,即所求二面角的余弦值是
,即所求二面角的余弦值是![]() . ………13分
. ………13分
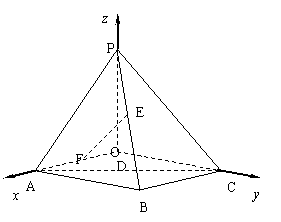
方法2:
如图,以点D为原点O,
有向直线OA、OC、OP分别为x、y、z轴
建立空间直角坐标系.
(Ⅰ)证明:因为![]() =(1,0,0),
=(1,0,0),
平面PAD的一个法向量为
rPAD=(0,1,0),
由![]() · rPAD=0,可得
· rPAD=0,可得![]() ⊥rPAD.
⊥rPAD.
于是BC∥平面PAD. ……………………………………………4分
(Ⅱ)证明:![]() =(0,-
=(0,-![]() ,-
,-![]() ),
),![]() =(1,0,0),
=(1,0,0),
因为![]() ·
·![]() =0,
=0,
所以EF⊥BC. …………………………………………………8分
(Ⅲ)解:容易求出平面PAD的一个法向量为rPAD=(0,1,0),
及平面PAC的一个法向量为rPAC=(1,1, 1),
因为rPAD· rPAC=1,rPAD=1,rPAC=![]() ,
,
所以cos<rPAD, rPAC>=![]() =
=![]() ,
,
即所求二面角的余弦值是![]() . …………………………………13分
. …………………………………13分
(18)解:(Ⅰ) 若![]() ,
,
则 ![]() =
=![]() . …………2分
. …………2分
令![]() ,即
,即![]() .则
.则![]() 或
或![]() .
.
∴![]() 的单调增区间是
的单调增区间是![]() ,
,![]() . ……………………………6分
. ……………………………6分
令![]() ,即
,即![]() .则
.则![]() .
.
∴![]() 的单调减区间是
的单调减区间是![]() . ……………………………………………8分
. ……………………………………………8分
(Ⅱ)![]() , 设切点为
, 设切点为![]() ,
,
则曲线![]() 在点P处的切线的斜率
在点P处的切线的斜率![]() . …10分
. …10分
由题意,知![]() 有解,
有解,
∴ ![]() 即
即![]() .
…………………………………………13分
.
…………………………………………13分
(19) 解:(Ⅰ)∵ N为AF的中点,且![]() ,
,
∴ MN垂直平分AF. …………………………………………1分
又点M在线段AE上,
∴ ![]() .
.![]() .
.
∵![]() , …………………………………………4分
, …………………………………………4分
∴ 点M的轨迹W是以E、F为焦点的椭圆,且半长轴![]() ,
,
半焦距![]() . ………………………………………………………………5分
. ………………………………………………………………5分
∴ ![]() .
.
∴ 点M的轨迹W的方程为![]() . …………………………………7分
. …………………………………7分
(Ⅱ)设![]() ,
,
∵ ![]() ,
,![]() ,
,
∴ 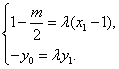 ∴
∴ 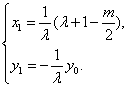 …………………9分
…………………9分
由点P、Q均在椭圆W上,
∴  ………………………………11分
………………………………11分
消去![]() 并整理,得
并整理,得![]() ,
,
∵![]() , ∴
, ∴![]() .
.
解得![]() .
…………………………………………………14分
.
…………………………………………………14分
(20)解:(Ⅰ)设第4列公差为![]() ,则
,则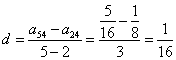 . ………2分
. ………2分
故![]() ,于是
,于是![]() .
.
由于![]() ,所以
,所以![]() ,故
,故![]() . …………………………………4分
. …………………………………4分
(Ⅱ)在第4列中,![]() . ………6分
. ………6分
由于第![]() 行成等比数列,且公比
行成等比数列,且公比![]() ,
,
所以, ![]() . ……………………8分
. ……………………8分
(Ⅲ)由(Ⅱ)可得![]() .即bn=
.即bn=![]() .
.
所以![]()
![]() .
.
即![]() , ………10分
, ………10分
故![]() . ……11分
. ……11分
两式相减,得![]() ……………12分
……………12分
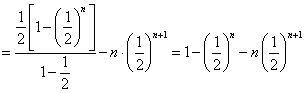 ,………13分
,………13分
所以![]() . …………………………………………………14分
. …………………………………………………14分
注:(1)2个空的填空题,第一个空给3分,第二个空给2分.
(2)如有不同解法,请阅卷老师酌情给分.