2006年高考数学复习易做易错题选
平面向量
一、选择题：
1．（如中）在
中,
,则
的值为
( )
A 20
B 
C 
D 
错误分析:错误认为
,从而出错.
答案: B
略解: 由题意可知
,
故=
.
2．（如中）关于非零向量
和
，有下列四个命题：
（1）“
”的充要条件是“和的方向相同”；
（2）“
” 的充要条件是“和的方向相反”；
（3）“” 的充要条件是“和有相等的模”；
（4）“
” 的充要条件是“和的方向相同”；
其中真命题的个数是 （ ）
A 1 B 2 C 3 D 4
错误分析:对不等式
的认识不清.
答案: B.
3．(石庄中学)已知O、A、B三点的坐标分别为O(0,0)，A(3，0)，B(0，3)，是P线段AB上且 
=t
(0≤t≤1)则
·
的最大值为 （ ）
A．3 B．6 C．9 D．12
正确答案：C 错因：学生不能借助数形结合直观得到当OPcosa最大时，· 即为最大。
4．(石庄中学)若向量 
=(cosa,sina) ， 
=
， 与不共线，则与一定满足（ ）
A． 与的夹角等于a-b B．∥
C．(+)^(-) D． ⊥
正确答案：C 错因：学生不能把、的终点看成是上单位圆上的点，用四边形法则来处理问题。
5．(石庄中学)已知向量 =(2cosj，2sinj)，jÎ(
)， =（0,-1)，则 与 的夹角为( )
A．
-j B．
+j C．j- D．j
正确答案：A 错因：学生忽略考虑与夹角的取值范围在[0，p]。
6．(石庄中学)O为平面上的定点，A、B、C是平面上不共线的三点，若( 
-
)·(+-2)=0，则DABC是（ ）
A．以AB为底边的等腰三角形 B．以BC为底边的等腰三角形
C．以AB为斜边的直角三角形 D．以BC为斜边的直角三角形
正确答案：B 错因：学生对题中给出向量关系式不能转化：2不能拆成(+)。
7．(石庄中学)已知向量M={ =(1,2)+l(3,4) lÎR}， N={=(-2,2)+ l(4,5) lÎR }，则MÇN=（ ）
A ｛（1，2）｝ B 
C 
D 
正确答案：C 错因：学生看不懂题意，对题意理解错误。
8．已知
，
，若
，则△ABC是直角三角形的概率是（ C ）
A．
B．
C．
D．
分析：由及知
，若
垂直，则
；若
与
垂直，则
，所以△ABC是直角三角形的概率是.
9．(磨中)设a0为单位向量，（1）若a为平面内的某个向量，则a=a·a0;(2)若a与a0平行，则a=a·a0；（3）若a与a0平行且a=1，则a=a0。上述命题中，假命题个数是（ ）
A.0 B.1 C.2 D.3
正确答案：D。
错误原因：向量的概念较多，且容易混淆，注意区分共线向量、平行向量、同向向量等概念。
10．(磨中)已知a=3,b=5，如果a∥b，则a·b= 。
正确答案：。±15。
错误原因：容易忽视平行向量的概念。a、b的夹角为0°、180°。
11．(磨中)O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足
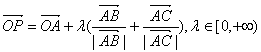,则P的轨迹一定通过△ABC的( )
(A)外心 (B)内心 (C)重心 (D)垂心
正确答案：B。
错误原因：对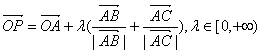
理解不够。不清楚
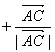与∠BAC的角平分线有关。
12．(磨中)如果
，那么
（ ） A．
B．
C． 
D．
在
方向上的投影相等
正确答案：D。
错误原因：对向量数量积的性质理解不够。
13．（城西中学）向量
＝（3，4）按向量a=(1,2)平移后为
（ ）
A、（4，6） B、（2，2） C、（3，4） D、（3，8）
正确答案： C
错因：向量平移不改变。
14．（城西中学）已知向量
则向量
的夹角范围是（ ）
A、[π/12，5π/12] B、[0，π/4] C、[π/4，5π/12] D、 [5π/12，π/2]
正确答案：A
错因：不注意数形结合在解题中的应用。
15．（城西中学）将函数y=2x的图象按向量 
平移后得到y=2x+6的图象，给出以下四个命题：① 的坐标可以是（-3，0）
②的坐标可以是（-3，0）和（0，6） ③的坐标可以是（0，6）
④的坐标可以有无数种情况，其中真命题的个数是
（ ）
A、1 B、2 C、3 D、4
正确答案：D
错因：不注意数形结合或不懂得问题的实质。
16．（城西中学）过△ABC的重心作一直线分别交AB,AC
于D,E,若
,(
),则
的值为( )
A 4 B 3 C 2 D 1
正确答案：A
错因：不注意运用特殊情况快速得到答案。
17．（蒲中）设平面向量
=(－2，1)，
=(λ，－1)，若与的夹角为钝角，则λ的取值范围是（ ）
A、
B、
C、
D、
答案：A
点评：易误选C，错因：忽视与反向的情况。
18．（蒲中）设=(x1，y1)，=(x2，y2)，则下列与共线的充要条件的有（ ）
① 存在一个实数λ，使=λ或=λ；
② ·= ；
③ 
；
④ (+)//(－)
A、1个 B、2个 C、3个 D、4个
答案：C
点评：①②④正确，易错选D。
19．（江安中学）以原点O及点A（5，2）为顶点作等腰直角三角形OAB，使
，则的坐标为（
）。
A、（2，-5） B、（-2，5）或（2，-5）
C、（-2，5） D、（7，-3）或（3，7）
正解：B
设
，则由
①
而又由
得
②
由①②联立得
。
误解：公式记忆不清，或未考虑到联立方程组解。
20．（江安中学）设向量
，则
是
的（
）条件。
A、充要 B、必要不充分
C、充分不必要 D、既不充分也不必要
正解：C
若则
，若，有可能
或
为0，故选C。
误解：
，此式是否成立，未考虑，选A。
21．（江安中学）在
OAB中，
，若
=-5，则
=（
）
A、
B、
C、
D、
正解：D。
∵∴
（LV为与的夹角）
∴
∴
∴
误解：C。将面积公式记错，误记为
22．（丁中）在中，
，
，有
，则的形状是
（D）
A、 锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
错解：C
错因：忽视中与的夹角是
的补角
正解：D
23．（丁中）设平面向量
，若与的夹角为钝角，则
的取值范围是 （A）
A、
B、（2，+
C、（—
D、（-
错解：C
错因：忽视使用时，其中包含了两向量反向的情况
正解：A
24．（薛中）已知A（3，7），B（5，2），向量
平移后所得向量是
。
A、（2，-5）， B、（3，-3）， C、（1，-7） D、以上都不是
答案：A
错解：B
错因：将向量平移当作点平移。
25．（薛中）已知
中，
。
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
答案：C
错解：A或D
错因：对向量夹角定义理解不清
26．（案中）正三角形ABC的边长为1，设
，那么
的值是
（ ）
A、
B、
C、
D、
正确答案：(B)
错误原因：不认真审题，且对向量的数量积及两个向量的夹角的定义模糊不清。
27．（案中）已知
，且
，则
（ ）
A、相等 B、方向相同 C、方向相反 D、方向相同或相反
正确答案：(D)
错误原因：受已知条件的影响，不去认真思考
可正可负，易选成B。
28．（案中）已知
是关于x的一元二次方程，其中
是非零向量，且向量
不共线，则该方程
（ ）
A、至少有一根 B、至多有一根
C、有两个不等的根 D、有无数个互不相同的根
正确答案：(B)
错误原因：找不到解题思路。
29．（案中）设是任意的非零平面向量且互不共线，以下四个命题：
①
②
③
④若
不平行
其中正确命题的个数是
（ ）
A、1个 B、2个 C、3个 D、4个
正确答案：(B)
错误原因：本题所述问题不能全部搞清。
二填空题：
1．（如中）若向量
=
，
=
，且，的夹角为钝角，则
的取值范围是______________.
错误分析：只由
的夹角为钝角得到
而忽视了
不是
夹角为钝角的充要条件,因为的夹角为
时也有从而扩大的范围,导致错误.
正确解法:
，的夹角为钝角, 
解得
或 
(1)
又由共线且反向可得
(2)
由(1),(2)得的范围是
答案: .
2．（一中）有两个向量
，
，今有动点
，从
开始沿着与向量
相同的方向作匀速直线运动，速度为
；另一动点
，从
开始沿着与向量
相同的方向作匀速直线运动，速度为
．设、在时刻
秒时分别在
、
处，则当
时，
秒．正确答案：2
（薛中）1、设平面向量
若
的夹角是钝角，则的范围是
。
答案：
错解：
错因：“
”与“
的夹角为钝角”不是充要条件。
3．（薛中）
是任意向量，给出：1
2
，3方向相反，4
5都是单位向量，其中
是共线的充分不必要条件。
答案：134
错解：13
错因：忽略
方向的任意性，从而漏选。
4．（案中）若
上的投影为
。
正确答案：
错误原因：投影的概念不清楚。
5．（案中）已知o为坐标原点，
集合
,且
。
正确答案：46
错误原因：看不懂题意，未曾想到数形结合的思想。
三、解答题：
1．（如中）已知向量
,且
求
(1) 
及
;
(2)若
的最小值是
,求实数的值.
错误分析:(1)求出=
后,而不知进一步化为
,人为增加难度;
(2)化为关于
的二次函数在
的最值问题,不知对对称轴方程讨论.
答案: (1)易求
, = ;
(2)
=
=
=
从而:当
时,
与题意矛盾, 不合题意;
当
时,
;
当
时,
解得
,不满足;
综合可得: 实数的值为
.
2．（如中）在中,已知
,且的一个内角为直角,求实数
的值.
错误分析:是自以为是,凭直觉认为某个角度是直角,而忽视对诸情况的讨论.
答案: (1)若
即
故
,从而
解得
;
(2)若
即
,也就是
,而
故
,解得
;
(3)若
即
,也就是
而
,故
,解得
综合上面讨论可知,或或
3．（石庄中学）已知向量m=(1,1)，向量
与向量
夹角为
，且·=-1，
(1)求向量；
(2)若向量与向量
=(1,0)的夹角为，向量
=(cosA,2cos2
)，其中A、C为DABC的内角，且A、B、C依次成等差数列，试求+的取值范围。
解：(1)设=(x,y)
则由<,>=得：cos<,>=
=
①
由·=-1得x+y=-1 ②
联立①②两式得
或
∴=(0,-1)或(-1,0)
(2) ∵<,>=
得·
=0
若=(1,0)则·=-1¹0
故¹(-1,0) ∴=(0,-1)
∵2B=A+C，A+B+C=p
ÞB=
∴C=
+=(cosA,2cos2
)
=(cosA,cosC)
∴+=
=
=
=
=
=
=
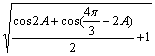
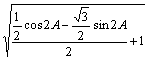
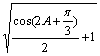
∵0<A<
∴0<2A<
∴-1<cos(2A+)<
∴+Î(
)
4．（石庄中学）已知函数f(x)=mx-1(mÎR且m¹0)设向量
)，
，
，
，当qÎ(0，
)时，比较f(
)与f(
)的大小。
解：=2+cos2q，=2sin2q+1=2-cos2q
f()=m1+cos2q=2mcos2q
f()=m1-cos2q=2msin2q
于是有f()-f()=2m(cos2q-sin2q)=2mcos2q
∵qÎ(0,) ∴2qÎ(0, ) ∴cos2q>0
∴当m>0时，2mcos2q>0，即f()>f()
当m<0时，2mcos2q<0，即f()<f()
5．（石庄中学）已知ÐA、ÐB、ÐC为DABC的内角，且f(A、B)=sin22A+cos22B-
sin2A-cos2B+2
(1)当f(A、B)取最小值时，求ÐC
(2)当A+B=时，将函数f(A、B)按向量平移后得到函数f(A)=2cos2A求
解：(1) f(A、B)=(sin22A-sin2A+
)+(cos22B-cos2B+
)+1
=(sin2A-
)2+(sin2B-)2+1
当sin2A=,sin2B=时取得最小值，
∴A=30°或60°，2B=60°或120° C=180°-B-A=120°或90°
(2) f(A、B)=sin22A+cos22(
)-
=
=
=
6．（石庄中学）已知向量
（m为常数），且,不共线，若向量,的夹角落< , >为锐角，求实数x的取值范围.
解：要满足<
>为锐角
只须
>0且
（
）
=
= 
=
即 x (mx-1) >0
1°当 m > 0时
x<0
或
2°m<0时
x ( -mx+1) <0
3°m=0时 只要x<0
综上所述：x > 0时，
x = 0时，
x < 0时，
7．(磨中)已知a=（cosα，sinα）,b=（cosβ,sinβ），a与b之间有关系ka+b=a－kb，其中k>0，
（1）用k表示a·b;
（2）求a·b的最小值，并求此时a·b的夹角的大小。
解 （1）要求用k表示a·b,而已知ka+b=a－kb，故采用两边平方，得
ka+b2=(a－kb)2
k2a2+b2+2ka·b=3(a2+k2b2－2ka·b)
∴8k·a·b=(3－k2)a2+(3k2－1)b2
a·b =
∵a=(cosα，sinα),b=(cosβ,sinβ)，
∴a2=1, b2=1,
∴a·b =
=
（2）∵k2+1≥2k，即≥
=
∴a·b的最小值为，
又∵a·b = a·b ·cos
，a=b=1
∴=1×1×cos。
∴=60°,此时a与b的夹角为60°。
错误原因：向量运算不够熟练。实际上与代数运算相同，有时可以在含有向量的式子左右两边平方，且有a+b2=(a+b)2=a2+b2+2a·b或a2+b2+2a·b。
8．（一中）已知向量
，
，
．
（Ⅰ）求
的值；
（Ⅱ）若
，
，且
，求
的值．
解（Ⅰ）
,
.
, 
,
即 
. 
.
（Ⅱ）
，
，
.
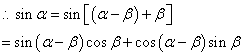
欢迎访问 http://www.k12zy.com