高考数学复习易做易错题选
数列部分
一、选择题:
1.(石庄中学)设s![]() 是等差数列{a
是等差数列{a![]() }的前n项和,已知s
}的前n项和,已知s![]() =36,
=36,![]() s
s![]() =324, s
=324, s![]() =144 (n>6),则n=( )
=144 (n>6),则n=( )
A 15 B
正确答案:D 错因:学生不能运用数列的性质计算a![]() +a
+a![]() =
=![]()
2.(石庄中学)已知s![]() 是等差数列{a
是等差数列{a![]() }的前n项和,若a
}的前n项和,若a![]() +a
+a![]() +a
+a![]() 是一个确定的常数,则数列{s
是一个确定的常数,则数列{s![]() }中是常数的项是( )
}中是常数的项是( )
A s![]() B s
B s![]() C s
C s![]() D s
D s![]()
正确答案: D 错因:学生对等差数列通项公式的逆向使用和等差数列的性质不能灵活应用。
3.(石庄中学)设{a![]() }是等差数列,{b
}是等差数列,{b![]() }为等比数列,其公比q≠1,
且b
}为等比数列,其公比q≠1,
且b![]() >0(i=1、2、3 …n) 若a
>0(i=1、2、3 …n) 若a![]() =b
=b![]() ,a
,a![]() =b
=b![]() 则 ( )
则 ( )
A a![]() =b
=b![]() B a
B a![]() >b
>b![]() C a
C a![]() <b
<b![]() D a
D a![]() >b
>b![]() 或 a
或 a![]() <b
<b![]()
正确答案 B 错因:学生不能灵活运用等差中项和等比中项的定义及基本不等式。
4.(石庄中学)已知非常数数列{a![]() },满足 a
},满足 a![]() -a
-a![]() a
a![]() +a
+a![]() =0且a
=0且a![]() ≠a
≠a![]() , i=1、2、3、…n,对于给定的正整数n,a
, i=1、2、3、…n,对于给定的正整数n,a![]() =a
=a![]() ,则
,则![]()
![]() 等于( )
等于( )
A 2 B
正确答案:D 错因:学生看不懂题目,不能挖掘题目的隐含条件,{a![]() }的项具有周期性。
}的项具有周期性。
5.(石庄中学)某人为了观看2008年奥运会,从2001年起每年5月10日到银行存入a元定期储蓄,若年利率为p且保持不变,并且每年到期的存款及利息均自动转为新一年定期,到2008年将所有的存款和利息全部取回,则可取回的钱的总数(元)为( ).
A a(1+p)![]() B a(1+p)
B a(1+p)![]() C
C ![]() D
D ![]() ]
]
正确答案:D 错因: 学生对存款利息的计算方法没掌握。
6.(搬中)一个只有有限项的等差数列,它的前5项的和为34,最后5项的和为146,所有项的和为234,则它的第七项等于( )
A. 22 B.
解:设该数列有![]() 项
项
且首项为![]() ,末项为
,末项为![]() ,公差为
,公差为![]()
则依题意有
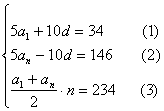
![]() 可得
可得
![]()
代入(3)有![]()
从而有![]()
又所求项![]() 恰为该数列的中间项,
恰为该数列的中间项,
![]()
故选D
说明:虽然依题意只能列出3个方程,而方程所涉及的未知数有4个,但将![]() 作为一个整体,问题即可迎刃而解。在求
作为一个整体,问题即可迎刃而解。在求![]() 时,巧用等差中项的性质也值得关注。知识的灵活应用,来源于对知识系统的深刻理解。
时,巧用等差中项的性质也值得关注。知识的灵活应用,来源于对知识系统的深刻理解。
7.(搬中)![]() 是
是![]() 成等比数列的( )
成等比数列的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解:![]() 不一定等比
不一定等比
如![]()
若![]() 成等比数列
成等比数列
则![]()
![]() 选D
选D
说明:此题易错选为A或B或C,原因是等比数列![]() 中要求每一项及公比
中要求每一项及公比![]() 都不为零。
都不为零。
8.(磨中)已知Sk表示{an}的前K项和,Sn—Sn+1=an(n∈N+),则{an}一定是_______。
A、等差数列 B、等比数列 C、常数列 D、以上都不正确
正确答案:D
错误原因:忽略an=0这一特殊性
9.(磨中)已知数列—1,a1,a2,—4成等差数列,—1,b1,b2,b3,—4成等比数列,则![]() 的值为___________。
的值为___________。
A、![]() B、—
B、—![]() C、
C、![]() 或—
或—![]() D、
D、![]()
正确答案:A
错误原因:忽略b2为等比数列的第三项,b2符号与—1、—4同号
10.(磨中)等比数列{an}的公比为q,则q>1是“对于任意n∈N+”都有an+1>an的_______条件。
A、必要不充分条件 B、充分不必要条件
C、充要条件 D、既不充分也不必要条件
正确答案:D
错误原因:忽略a1与q共同限制单调性这一特性
11.(城西中学)数列![]() 的前n项和为s
的前n项和为s![]() =n2+2n-1,
=n2+2n-1,
则a1+a3+a5+……+a25=( )
A 350 B 351 C 337 D 338
正确答案:A
错因:不理解该数列从第二项起向后成等差数列。
12.(城西中学)在等差数列![]() ,则在Sn中最大的负数为( )
,则在Sn中最大的负数为( )
A.S17 B.S18 C.S19 D.S20
答案:C
错因:等差数列求和公式应用以及数列性质分析错误。
13.(城西中学)已知三个互不相等实数![]() 成等差数列,那么关于
成等差数列,那么关于![]() 的方程
的方程![]()
A,一定有两个不相等的实数根 B,一定有两个相等的实数根
C, 一定没有实数根 D,一定有实数根
正确答案:D
错因:不注意a=0的情况。
14.(城西中学)从集合{1,2,3,…,10}中任意选出三个不同的数,使这三个数成等比数列,这样的等比数列个数为( )
A.3 B.4 C.6 D.8
正确答案:D
错因:误认为公比一定为整数。
15.(城西中学)若干个能唯一确定一个数列的量称为该数列的“基本量”,设![]() 是公比为q的无穷等比数列,下列四组量中,一定能成为数列
是公比为q的无穷等比数列,下列四组量中,一定能成为数列![]() “基本量”的是( )
“基本量”的是( )
(1)![]() ,(2)
,(2)![]() (3)
(3)![]() ,
,![]() ,(4)
,(4)![]()
A.(1)(3) B .(1) (4) C.(2) (3) D.(2)(4)
正确答案(B)
错因:题意理解不清
16.(城西中学)已知等差数列{an,}的前n项和为sn,且S2=10,S5=55,则过点P(n,),Q(n+2,)(n∈N+*)的直线的斜率为
A、4 B、3 C、2 D、1
正确答案: D
错因:不注意对和式进行化简。
17.(城西中学)在![]() 之间插入n个正数,使这n+2个正数成等比数列,则插入的n个正数之积为._______.
之间插入n个正数,使这n+2个正数成等比数列,则插入的n个正数之积为._______.
正确答案:![]()
错因:无法探求问题实质,致使找不到解题的切入点。
18.(城西中学)数列![]() 满足
满足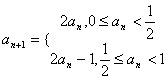 ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
正确答案:C
错因:缺研究性学习能力
19.(一中)已知数列![]() 的前n项和为
的前n项和为![]() ,
,![]() ,现从前m项:
,现从前m项:![]() ,
,![]() ,…,
,…,![]() 中抽出一项(不是
中抽出一项(不是![]() ,也不是
,也不是![]() ),余下各项的算术平均数为37,则抽出的是
),余下各项的算术平均数为37,则抽出的是
A.第6项 B.第8项 C.第12项 D.第15项
正确答案:B
20.(一中)某种细菌![]() 在细菌
在细菌![]() 的作用下完成培养过程,假设一个细菌
的作用下完成培养过程,假设一个细菌![]() 与一个细菌
与一个细菌![]() 可繁殖为2个细菌
可繁殖为2个细菌![]() 与0个细菌
与0个细菌![]() ,今有1个细菌
,今有1个细菌![]() 和512个细菌
和512个细菌![]() ,则细菌
,则细菌![]() 最多可繁殖的个数为
最多可繁殖的个数为
A.511 B.512 C.513 D.514
正确答案:C
21.(一中)等比数列![]() 中,
中,![]() ,公比
,公比![]() ,用
,用![]() 表示它前n项的积:
表示它前n项的积:![]() ,则
,则![]()
![]()
![]() 中最大的是( )
中最大的是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
正确答案:C
22.(一中)已知![]() ,对于
,对于![]() ,定义
,定义![]() ,
,![]() 假设
假设![]() ,那么
,那么![]() 解析式是( )
解析式是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
正确答案:B
|
① ② ③
根据图中花盆摆放的规律,猜想第![]() 个图形中花盆的盆数
个图形中花盆的盆数![]() =
.
=
.
正确答案:![]()
24.(一中)![]() 是实数构成的等比数列,Sn是其前n项和,则数列
是实数构成的等比数列,Sn是其前n项和,则数列![]() 中
( )
中
( )
A、任一项均不为0 B、必有一项为0
C、至多有有限项为0 D、或无一项为0,或无穷多项为0
正确答案:D
25.(蒲中)![]() 是a,x,b成等比数列的( )
是a,x,b成等比数列的( )
A、充分非必要条件 B、必要非充分条件
C、充要条件 D、既不充分又不必要条件
答案:D
点评:易错选A或B。
26.(蒲中)数列1,1+2,1+2+4,…,1+2+4+…+2n各项和为( )
A、2n+1-2-n B、2n-n-1
C、2n+2-n-3 D、2n+2-n-2
答案:C
点评:误把1+2+4+…+2n当成通项,而忽略特值法排除,错选A。
27.(蒲中)已知数列{an}的通项公式为an=6n-4,数列{bn}的通项公式为bn=2n,则在数列{an}的前100项中与数列{bn}中各项中相同的项有( )
A、50项 B、34项 C、6项 D、5项
点评:列出两个数列中的项,找规律。
28.(江安中学)已知数列![]() 中,若
中,若![]() ≥2),则下列各不等式中一定成立的是(
)。
≥2),则下列各不等式中一定成立的是(
)。
A.
![]() ≤
≤![]()
B.
![]()
C.
![]() ≥
≥![]()
D.
![]()
正解:A
由于![]() ≥2),
≥2),![]()
![]() 为等差数列。
为等差数列。![]()
而![]()
![]()
![]() ≤0
≤0 ![]()
![]() ≤
≤![]()
误解:判断不出等差数列,判断后,是否选用作差法。
29.(江安中学)某工厂第一年年产量为A,第二年的增长率为a,第三年的增长率为b,这两年的平均增长率为x,则( )。
E.
![]()
F.
![]() ≤
≤![]()
G.
![]() >
>![]()
H.
![]() ≥
≥![]()
正解:B
设平均增长率为![]() ,
,
![]()
![]()
![]() ≤
≤![]()
![]()
误解:![]()
![]()
![]()
![]()
30.(江安中学)计算机是将信息转换成二进制进行处理的,二进制即“逢二进一”,如(1101)2表示二进制数,将它转换成十进制形式,是![]() ,那么二进制数
,那么二进制数![]() 转换成十进制形式是(
)
转换成十进制形式是(
)
I. 217-2
J. 216-2
K. 216-1
L. 215-1
正解:C
![]() =
=![]()
误解:①没有弄清题意;②![]() =
=![]()
31.(江安中学)在数列{![]() }中,
}中,![]() ,则
,则![]() 等于(
)。
等于(
)。
M.
![]()
N. 10
O. 13
P. 19
正解:C。由2![]() 得
得![]() ,∴{
,∴{![]() }是等差数列
}是等差数列
∵![]()
![]()
误解:A、B、D被式子![]() 的表面所迷惑,未发现{
的表面所迷惑,未发现{![]() }是等差数列这个本质特征,而只由表面的递推关系得到,从而计算繁琐,导致有误。
}是等差数列这个本质特征,而只由表面的递推关系得到,从而计算繁琐,导致有误。
32.(江安中学)已知等比数列{![]() }的首项为
}的首项为![]() ,公比为q,且有
,公比为q,且有![]() ,则首项
,则首项![]() 的取值范围是(
)。
的取值范围是(
)。
Q.
![]()
R.
![]()
S.
![]()
T.
![]()
正解:D。 ![]() ①
①![]() 时,
时,![]() ,
,![]() ;
;
②![]() 且
且![]() 时
时![]()
![]()
![]() 且
且![]() ,
,![]() 。
。![]() 选
选![]() 。
。
误解:①没有考虑![]() ,忽略了
,忽略了![]() ;
;
②对![]() ,只讨论了
,只讨论了![]() 或
或![]() ,或
,或![]() ,而得到了错误解答。
,而得到了错误解答。
33.(江安中学)在![]() ABC中,
ABC中,![]() 为
为![]() 的对边,且
的对边,且![]() ,则(
)。
,则(
)。
U.
![]() 成等差数列
成等差数列
V.
![]() 成等差数列
成等差数列
W.
![]() 成等比数列
成等比数列
X.
![]() 成等比数列
成等比数列
正解:D。
![]()
![]()
即![]()
![]() ,
,![]()
![]()
注意:切入点是将![]() 恒等变形,若找不准,将事倍功半。
恒等变形,若找不准,将事倍功半。
34.(丁中)x=![]() 是a、x、b成等比数列的(
是a、x、b成等比数列的(
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
错解:C或A
错因:①误认为x=![]() 与
与![]() 。②忽视
。②忽视![]() 为零的情况。
为零的情况。
正解:D
35.(丁中)若![]() 成等比数列,则下列三个数:①
成等比数列,则下列三个数:①![]()
②![]() ③
③![]() ,必成等比数列的个数为( )
,必成等比数列的个数为( )
A、3 B、2 C、1 D、0
错解: A.
错因:没有考虑公比![]() 和
和![]() 的情形,将①③也错认为是正确的.
的情形,将①③也错认为是正确的.
正解: C.
36.(丁中)已知![]() 是递增数列,且对任意
是递增数列,且对任意![]() 都有
都有![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围
(D)
的取值范围
(D)
A、(![]() B、(
B、(![]() C、(
C、(![]() D、(
D、(![]()
错解:C
错因:从二次函数的角度思考,用![]()
正解:D。
37.(丁中)等比数列![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() 的值
的值
(A)是3或-3 (B)
是3 (C)
是-3 (D)不存在
错解:A
错因:直接![]() ,
,![]() ,
,![]() 成等比数列,
成等比数列,![]() ,忽视这三项要同号。
,忽视这三项要同号。
正解:C
38.(薛中)数列![]() 的前n项和
的前n项和![]() .
.
A、350 B、351 C、337 D、338
答案:A
错解:B
错因:首项不满足通项。
39.(薛中)在等差数列![]() 中,
中,![]() ,若它的前n项和Sn有最大值,那么
,若它的前n项和Sn有最大值,那么![]() 中的最小正数是( )
中的最小正数是( )
A、S17 B、S18 C、S19 D、S20
答案:C
错解:D
错因:![]() 化简时没有考虑a10的正负。
化简时没有考虑a10的正负。
40.(薛中)若a,b,a+b成等差数列,a,b,ab成等比数列,且![]() ,则m 的取值范围是( )
,则m 的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
答案:C
错解:B
错因:对数函数的性质不熟。
41.(薛中)已知数列![]() 的通项公式为
的通项公式为![]() ,则关于an的最大,最小项,叙述正确的是( )
,则关于an的最大,最小项,叙述正确的是( )
A、最大项为a1,最小项为a3 B、最大项为a1,最小项不存在
C、最大项不存在,最小项为a3 D、最大项为a1,最小项为a4
答案:A
错解:C
错因:没有考虑到![]() 时,
时,![]()
42.(案中)等比数列![]()
![]() 的等比中项为( )
的等比中项为( )
A、16 B、±16 C、32 D、±32
正确答案:(B)
错误原因:审题不清易选(A),误认为是![]() ,实质为±
,实质为±![]() 。
。
43.(案中)已知![]() 的前n项之和
的前n项之和![]() …
…![]() 的值为 ( )
的值为 ( )
A、67 B、65 C、61 D、55
正确答案:A
错误原因:认为![]() 为等差数列,实质为
为等差数列,实质为![]()
二填空题:
1.(如中)在等比数列![]() 中,若
中,若![]() 则
则![]() 的值为____________
的值为____________
[错解]![]() 或
或![]()
[错解分析] 没有意识到所给条件隐含公比为正
[正解]![]()
2.(如中)实数项等比数列![]() 的前
的前![]() 项的和为
项的和为![]() ,若
,若![]() ,则公比
,则公比![]() 等于________-
等于________-
[错解]![]()
[错解分析]用前![]() 项的和公式求解本题,计算量大,出错,应活用性质
项的和公式求解本题,计算量大,出错,应活用性质
[正解]![]()
3.(如中)从集合![]() 中任取三个不同的数,使这三个数成等差数列,这样的等差数列最多有_________
中任取三个不同的数,使这三个数成等差数列,这样的等差数列最多有_________
[错解]90个
[错解分析]没有考虑公差为负的情况,思考欠全面
[正解]180个
4.(如中)设数列![]() 满足
满足![]() ,则
,则![]() 为等差数列是
为等差数列是![]() 为等比数列的____________条件
为等比数列的____________条件
[错解]充分
[错解分析] 对数运算不清,判别方法没寻求到或半途而废
[正解]充要
5.(如中)若数列![]() 是等差数列,其前
是等差数列,其前![]() 项的和为
项的和为![]() ,则
,则![]() 也是等差数列,类比以上性质,等比数列
也是等差数列,类比以上性质,等比数列![]() ,则
,则![]() =__________,
=__________,![]() 也是等比数列
也是等比数列
[错解]![]()
[错解分析] 没有对![]() 仔细分析,其为算术平均数,
仔细分析,其为算术平均数,
[正解]![]()
6.(如中)已知数列![]() 中,
中,![]() 则
则![]() 等于______________
等于______________
[错解]![]() 或
或 ![]() 或
或![]()
[错解分析] 盲目下结论,没能归纳出该数列项的特点
[正解]![]()
7.(如中)已知数列![]() 中,
中,![]() (
(![]() 是与
是与![]() 无关的实数常数),且满足
无关的实数常数),且满足![]() ,则实数
,则实数![]() 的取值范围是___________
的取值范围是___________
[错解]![]()
[错解分析]审题不清,若能结合函数分析会较好
[正解]![]()
8.(如中)一种产品的年产量第一年为![]() 件,第二年比第一年增长
件,第二年比第一年增长![]() ﹪,第三年比第二年增长
﹪,第三年比第二年增长![]() ﹪,且
﹪,且![]() ,若年平均增长
,若年平均增长![]() ﹪,则有
﹪,则有![]() ___
___![]() (填
(填![]() )
)
[错解]![]()
[错解分析]实际问题的处理较生疏,基本不等式的使用不娴熟
[正解]![]()
9.(城西中学)给定![]() ,定义使
,定义使![]() 为整数的
为整数的![]() 叫做“企盼数”,则在区间(1,62)内的所有企盼数的和是___________.
叫做“企盼数”,则在区间(1,62)内的所有企盼数的和是___________.
正确答案:52
错因:大部分学生难以读懂题意,也就难以建立解题数学模型。
10.(蒲中)数列{an}的前n项和Sn=n2+1,则an=____________
答案:an=![]()
![]()
点评:误填2n-1,忽略“an=Sn-Sn-1”成立的条件:“n≥2”。
11.(蒲中)已知{an}为递增数列,且对于任意正整数n,an=-n2+λn恒成立,则λ的取值范围是____________
答案:λ>3
点评:利用二次函数单调性讨论较繁,且易错,利用an+1>an恒成立较方便。
12.(江安中学)关于数列有下列四个判断:
1)
若![]() 成等比数列,则
成等比数列,则![]() 也成等比数列;
也成等比数列;
2)
若数列{![]() }既是等差数列也是等比数列,则{
}既是等差数列也是等比数列,则{![]() }为常数列;
}为常数列;
3)
数列{![]() }的前n项和为
}的前n项和为![]() ,且
,且![]() ,则{
,则{![]() }为等差或等比数列;
}为等差或等比数列;
4)
数列{![]() }为等差数列,且公差不为零,则数列{
}为等差数列,且公差不为零,则数列{![]() }中不会有
}中不会有![]() ,其中正确判断的序号是______(注:把你认为正确判断的序号都填上)
,其中正确判断的序号是______(注:把你认为正确判断的序号都填上)
正解:(2)(4).
误解:(1)(3)。对于(1)a、b、c、d成等比数列。![]()
![]()
![]()
![]() 也成等比数列,这时误解。因为特列:
也成等比数列,这时误解。因为特列:![]() 时,
时,![]() 成等比数列,但
成等比数列,但![]() ,
,![]() ,
,![]() ,即
,即![]() 不成等比。
不成等比。
对于(3)可证当![]() 时,为等差数列,
时,为等差数列,![]() 时为等比数列。
时为等比数列。![]()
![]() 时既不是等差也不是等比数列,故(3)是错的。
时既不是等差也不是等比数列,故(3)是错的。
13.(江安中学)关于![]() 的方程
的方程![]() 的所有实根之和为_____。
的所有实根之和为_____。
正解:168
![]() 方程有实根,
方程有实根,
![]()
![]() ≥0
≥0
解得:![]() ≤n≤
≤n≤![]()
![]()
![]() 所有实根之和为
所有实根之和为![]()
误解:没能根据条件具体确定n的取值,只得出一个关于n的多项式结果。
14.(江安中学)有四个命题:
1)
一个等差数列{![]() }中,若存在
}中,若存在![]() ,则对于任意自然数
,则对于任意自然数![]() ,都有
,都有![]() ;
;
2)
一个等比数列{![]() }中,若存在
}中,若存在![]() ,则对于任意
,则对于任意![]() ,都有
,都有![]() ;
;
3)
一个等差数列{![]() }中,若存在
}中,若存在![]() ,则对于任意
,则对于任意![]() ,都有
,都有![]() ;
;
4)
一个等比数列{![]() }中,若存在自然数
}中,若存在自然数![]() ,使
,使![]() ,则对于任意
,则对于任意![]() ,都有
,都有![]() ,其中正确命题的序号是_____。
,其中正确命题的序号是_____。
正解:由等差数列和等比数列的性质得①②④。
误解:“对于等比数列,若![]() ,各项同号(同正或同负),若
,各项同号(同正或同负),若![]() ,各项正,负相间”,学生对此性质把握不清,故认为②④错。
,各项正,负相间”,学生对此性质把握不清,故认为②④错。
15.(丁中)已知数列{an}的前n项和Sn=an-1(a![]() ),则数列{an}_______________
),则数列{an}_______________
A.一定是等差数列 B.一定是等比数列
C.或者是等差数列或者是等比数列 D.既非等差数列又非等比数列
错解:B
错因:通项![]() 中忽视
中忽视![]() 的情况。
的情况。
正解:C
16.(丁中)设等差数列![]() 中,
中,![]() ,且从第5项开始是正数,则公差的范围是
,且从第5项开始是正数,则公差的范围是
![]()
错解:![]()
错因:忽视![]() ,即第4项可为0。
,即第4项可为0。
正解:![]()
17.(丁中)方程![]() 的四个实数根组成一个首项为
的四个实数根组成一个首项为![]() 的等比数列,则
的等比数列,则![]()
正解: ![]() .
.
错因:设方程![]() 的解为
的解为![]() ;方程
;方程![]() 的解为
的解为![]() ,则
,则![]() ,不能依据等比数列的性质准确搞清
,不能依据等比数列的性质准确搞清![]() 的排列顺序.
的排列顺序.
18.(丁中)等差数列{an}中, a1=25, S17=![]() ,则该数列的前__________项之和最大,其最大值为_______。
,则该数列的前__________项之和最大,其最大值为_______。
错解:12
错因:忽视![]()
正解:12或13 , ![]()
19.(薛中)若![]() ,则数列
,则数列![]() 的前n项和Sn=
。
的前n项和Sn=
。
答案:![]()
错解:![]()
错因:裂项求和时系数2丢掉。
20.(薛中)已知数列![]() 是非零等差数列,又a1,a3,a9组成一个等比数列的前三项,则
是非零等差数列,又a1,a3,a9组成一个等比数列的前三项,则![]() 的值是
。
的值是
。
答案:1或![]()
错解:![]()
错因:忘考虑公差为零的情况。
21.(薛中)对任意正整数n, ![]() 满足数列是递增数列,则
满足数列是递增数列,则![]() 的取值范围是
。
的取值范围是
。
答案:![]()
错解:![]()
错因:利用二次函数的对称轴,忽视其与![]() 的关系。
的关系。
22.(案中)数列![]() 的前n项之和为
的前n项之和为![]() ,若将此数列按如下规律编组:(
,若将此数列按如下规律编组:(![]() )、(
)、(![]() ,
,![]() )、(
)、(![]() ,
,![]() ,
,![]() )、……,则第n组的n个数之和为
。
)、……,则第n组的n个数之和为
。
正确答案:![]()
错误原因:未能明确第n组各项的构成规律,尤其是首项和最后一项,从而找不到合适的解法,应转化为:![]()
23.(案中)若an=1+2+3+…+n,则数列![]() 的前n项之和
的前n项之和![]() =
。
=
。
正确答案:![]()
错误原因:未能将an先求和得![]() 不强。
不强。
24.(案中)若数列![]() 为等差数列且
为等差数列且![]() ,则数列
,则数列![]() ,类比上述性质,相应地若数列
,类比上述性质,相应地若数列![]() >0,
>0,![]() ,则有
,则有![]()
正确答案:![]()
错误原因:类比意识不强
三、解答题:
1.(如中)设数列的前![]() 项和为
项和为![]() ,求这个数列的通项公公式
,求这个数列的通项公公式
[错解] 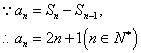
[错解分析]此题错在没有分析![]() 的情况,以偏概全.误认为任何情况下都有
的情况,以偏概全.误认为任何情况下都有![]()
[正解] ![]()
因此数列的通项公式是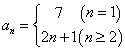
2.(如中)已知一个等比数列![]() 前四项之积为
前四项之积为![]() ,第二、三项的和为
,第二、三项的和为![]() ,求这个等比数列的公比.
,求这个等比数列的公比.
[错解]![]() 四个数成等比数列,可设其分别为
四个数成等比数列,可设其分别为![]()
则有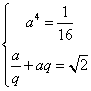 ,解得
,解得![]() 或
或![]() ,
,
故原数列的公比为![]() 或
或![]()
[错解分析]按上述设法,等比数列公比![]() ,各项一定同号,而原题中无此条件
,各项一定同号,而原题中无此条件
[正解]设四个数分别为![]()
则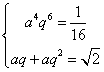 ,
,
![]()
由![]() 时,可得
时,可得![]()
当![]() 时,可得
时,可得![]()
3.(石庄中学) 已知正项数{an}满足a1= a (0<a<1) ,且![]()
![]() ,求证:
,求证:
(I) ![]() ; (II)
; (II)
![]() .
.
解析:(I) 将条件![]() 变形,得
变形,得![]() .
.
于是,有![]() ,
,![]() ,
,![]() ,……
,……![]() .
.
将这n-1个不等式叠加,得![]() ,故
,故![]() .
.
(II) 注意到0<a<1,于是由(I)得![]() =
=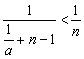 ,
,
从而,有![]()
![]()
![]() .
.
4.(搬中) 已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
解:![]()
![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
![]() 的通项公式为
的通项公式为
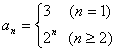
说明:此题易忽略![]() 的情况。
的情况。![]() 应满足条件
应满足条件![]() 。
。
5.(搬中)等比数列![]() 的前
的前![]() 项和为
项和为![]() ,求公比
,求公比![]() 。
。
解:若![]()
则![]()
![]()
![]() 矛盾
矛盾
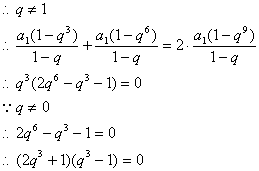
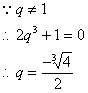
说明:此题易忽略![]() 的情况,在等比数列求和时要分公比
的情况,在等比数列求和时要分公比![]() 两种情况进行讨论。
两种情况进行讨论。
6.(搬中)求和![]() 。
。
解:若![]()
则![]()
若![]()
则![]()
若![]()
且![]()
令![]()
则![]()
两式相减得
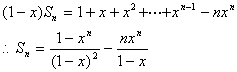
说明:此题易忽略前两种情况。数列求和时,若含有字母,一定要考虑相应的特殊情况。
7.(磨中)已知数列{an}的前n项和Sn=n2—16n—6,求数列{an}的前n项和Sn’
![]() 正确答案:Sn’= —n2+16n+6 n≤8时
正确答案:Sn’= —n2+16n+6 n≤8时
n2—16n+134 n>8时
错误原因:运用或推导公式时,只考虑一般情况,忽视特殊情况,导致错解。
8.(磨中) 已知函数f(x)= —Sin2x—aSinx+b+1的最大值为0,最小值—4 ,若实数a>0,求a、b的值。
正确答案:a=2 b= —2
错误原因:忽略对区间的讨论。
9.(磨中)数列{an}的前n项和Sn=n2—7n—8求数列通项公式
![]() 正确答案:an= —14 n=1
正确答案:an= —14 n=1
2n—8 n≥2
错误原因: n≥2时,an=Sn—Sn—1 但n=1时,不能用此式求出a1
10.(磨中)求和(x+![]() )2+(x2+
)2+(x2+![]() )2+……(xn+
)2+……(xn+![]() )2
)2
正确答案:当x2=1时 Sn=4n
当x2≠1时 Sn=![]() +2n
+2n
错误原因:应用等比数列求和时未考虑公比q是否为1
11.(城西中学)学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A![]() 、B
、B![]() 分别表示在第n个星期一选A、B菜的人数。(1)试以A
分别表示在第n个星期一选A、B菜的人数。(1)试以A![]() 表示A
表示A![]() ;(2)若A
;(2)若A![]() =200,求{A
=200,求{A![]() }的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
}的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
正确答案:(1)由题可知,![]() ,又
,又![]() ;
;
所以整理得:![]() 。(2)若A
。(2)若A![]() =200,且
=200,且![]() ,则设
,则设![]() 则
则![]() ,
,
∴![]() 即{A
即{A![]() -600}可以看成是首项为-400,公比为
-600}可以看成是首项为-400,公比为![]() 的等比数列。
的等比数列。
∴![]() ;(3)∵
;(3)∵![]() ,又
,又![]() 则
则![]() , 由
, 由![]() 得
得![]() 。即第3个星期一时,选A与选B的人数相等。
。即第3个星期一时,选A与选B的人数相等。
错因:不会处理非等差非等比数列。
12.(城西中学)设二次函数f(x)=x2+x,当x![]() [n,n+1](n
[n,n+1](n![]() +)时,f(x)的所有整数值的个数为g(n).
+)时,f(x)的所有整数值的个数为g(n).
(1) 求g(n)的表达式;
(2)
设an=![]() ( n
( n![]() +),Sn=a1-a2+a3-a4+…+(-1)n-1an,求Sn;
+),Sn=a1-a2+a3-a4+…+(-1)n-1an,求Sn;
(3)
设bn=![]() ,Tn=b1+b2+…+bn,
若Tn<L( L
,Tn=b1+b2+…+bn,
若Tn<L( L![]() ),求L的最小值。
),求L的最小值。
正确答案:(1)当x![]() [n,n+1](n
[n,n+1](n![]() +)时,函数f(x)=x2+x的值随x的增大而增大,则f(x)的值域为
+)时,函数f(x)=x2+x的值随x的增大而增大,则f(x)的值域为![]() (n
(n![]() +)
+)![]() (n
(n![]() +)
+)
(2)![]()
① 当n为偶数时
![]()
=![]()
②当n为奇数时
![]()
![]()
=![]()
∴![]()
(3)由![]() ,得
,得![]() ①
①
①×![]() 得:
得:![]() ②
②
①-②得 ![]()
则由![]() ﹤L( L
﹤L( L![]() ),L的最小值为7。
),L的最小值为7。
错因:1、①中整数解的问题
2、②运算的技巧
3、运算的能力
12.(薛中)已知数列![]() 中,a1=8, a4=2且满足
中,a1=8, a4=2且满足![]() (1)求数列
(1)求数列![]() 的
的
通项公式(2)设![]() ,求Sn
,求Sn
(3)设![]() ,是否存在最大的整数m,使得对任意
,是否存在最大的整数m,使得对任意![]() 均有
均有![]() 成立?若存在,求出m,若不存在,请说明理由。
成立?若存在,求出m,若不存在,请说明理由。
答案:(1)![]()
![]() (2)Sn=
(2)Sn= ![]()
![]()
(3)由(1)可得![]()
![]()
![]() 由Tn为关于n的增函数,故
由Tn为关于n的增函数,故![]() ,于是欲使
,于是欲使![]() 对
对![]() 恒成立,则
恒成立,则![]() 存在最大的整数m=7满足题意。
存在最大的整数m=7满足题意。
错因:对(2)中![]() 表达式不知进行分类讨论;对(3)忽视讨论Tn的单调性。
表达式不知进行分类讨论;对(3)忽视讨论Tn的单调性。
13.(蒲中)已知数列{an}的前n项和为Sn,且满足an+2Sn·Sn—1=0(n≥2),a1=![]() ,
,
(1)求证:![]() 成等差数列;(2)求an的表达式。
成等差数列;(2)求an的表达式。
解:(1)当n≥2时,an=Sn-Sn-1,又an+2SnSn-1=0,∴Sn-Sn-1+SnSn-1=0
若Sn=0,则a1=S1=0与a1=![]() 矛盾,∴Sn≠0,∴
矛盾,∴Sn≠0,∴![]() ,又
,又![]()
∴ ![]() 成等差数列。
成等差数列。
(2)由(1)知:![]() ,
,![]()
当n≥2时,an=-2SnSn-1=-![]() ,当n=1时,a1=
,当n=1时,a1=![]()
∴ 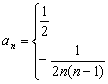
![]()
点评:本题易错点忽视公式an=Sn-Sn-1成立的条件“n≥2”,导致(2)的结果![]()
14.(江安中学)设![]() 为常数,且
为常数,且![]()
1)
证明对任意![]() ≥
≥![]() ;
;
2)
假设对任意n≥1有![]() ,求
,求![]() 的取值范围
的取值范围
证明:①设![]()
用![]() 代入,解出:
代入,解出:![]()
![]() 是公比为-2,首项为
是公比为-2,首项为![]() 的等比数列。
的等比数列。
![]()
![]()
![]() ,即
,即![]()
②若![]()
![]() 成立,特别取
成立,特别取![]() 有
有
![]()
![]()
![]()
下面证明![]() 时,对任意
时,对任意![]() ,有
,有![]()
由![]() 通项公式
通项公式
![]() ,
,
i)
当![]() 时,
时,
![]()
ii) 当![]() 时,
时,
![]() ≥0
≥0
故![]() 的取值范围为
的取值范围为![]()
误解:①对于等比数列:![]() 先构造出
先构造出![]() 求
求![]() ,难度较大,若用数学归纳法证明同学容易想到。
,难度较大,若用数学归纳法证明同学容易想到。
②通过对n为奇数或为偶数的讨论找出![]() 的取值范围有难度。
的取值范围有难度。
欢迎访问 http://www.k12zy.com