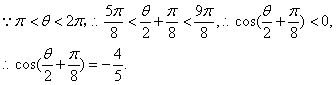高考高三数学寒假作业

高三数学寒假作业（1）参考答案

1、A　　　　  2、B　　　　3、C　　　　4、1<k<3　　 5、 0<a<

6、[解](1) 抛物线y²=2px的准线为x=-,于是4+=5, ∴p=2.

　 ∴抛物线方程为y²=4x.

　 (2)∵点A是坐标是(4,4), 由题意得B(0,4),M(0,2),

　 又∵F(1,0), ∴k_FA=;MN⊥FA, ∴k_MN=-,

　 则FA的方程为y=(x-1),MN的方程为y-2=-x,解方程组得x=,y=,

　 ∴N的坐标(,).

(1)　  由题意得, ,圆M.的圆心是点(0,2), 半径为2,

当m=4时, 直线AK的方程为x=4,此时,直线AK与圆M相离.

当m≠4时, 直线AK的方程为y=(x-m),即为4x-(4-m)y-4m=0,

圆心M(0,2)到直线AK的距离d=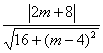,令d>2,解得m>1

∴当m>1时, AK与圆M相离;

　当m=1时, AK与圆M相切;

　当m<1时, AK与圆M相交.

高三数学寒假作业（2）参考答案

1、A　　　　  2、D　　　　3、D　　　　4、12　　  5、②③　　　　　 

6、[解](1)设中低价房面积形成数列{a_n},由题意可知{a_n}是等差数列,

　 其中a₁=250,d=50,则S_n=250n+=25n²+225n,

　 令25n²+225n≥4750,即n²+9n-190≥0,而n是正整数, ∴n≥10.

到2013年底,该市历年所建中低价房的累计面积将首次不少于4750万平方米.

(2)设新建住房面积形成数列{b_n},由题意可知{b_n}是等比数列,

其中b₁=400,q=1.08,则b_n=400·(1.08)^n-1·0.85.

　 由题意可知a_n>0.85 b_n,有250+(n-1)·50>400·(1.08)^n-1·0.85.

　 由计箅器解得满足上述不等式的最小正整数n=6.

　 到2009年底,当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%.

高三数学寒假作业（3）参考答案

1、C　　　　  2、C　　　　3、C　　　　4、155　　　　5、①③④

6、方案一：（Ⅰ）证明：∵PA⊥面ABCD，CD⊥AD，

∴由三垂线定理得：CD⊥PD.

因而，CD与面PAD内两条相交直线AD，PD都垂直，

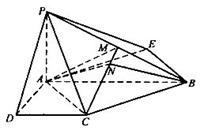∴CD⊥面PAD.

又CD面PCD，∴面PAD⊥面PCD.

（Ⅱ）解：过点B作BE//CA，且BE=CA，

则∠PBE是AC与PB所成的角.

连结AE，可知AC=CB=BE=AE=，又AB=2，

所以四边形ACBE为正方形.　由PA⊥面ABCD得∠PEB=90°

在Rt△PEB中BE=，PB=，　　

（Ⅲ）解：作AN⊥CM，垂足为N，连结BN.在Rt△PAB中，AM=MB，又AC=CB，

∴△AMC≌△BMC,∴BN⊥CM，故∠ANB为所求二面角的平面角.

∵CB⊥AC，由三垂线定理，得CB⊥PC，在Rt△PCB中，CM=MB，所以CM=AM.

在等腰三角形AMC中，AN·MC=，

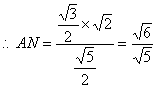.　　∴AB=2，

故所求的二面角为

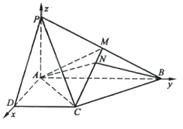
方法二：因为PA⊥PD，PA⊥AB，AD⊥AB，以A为坐标原点AD长为单位长度，如图建立空间直角坐标系，则各点坐标为

A（0，0，0）B（0，2，0），C（1，1，0），D（1，0，0），P（0，0，1），M（0，1，.

（Ⅰ）证明：因

又由题设知AD⊥DC，且AP与与AD是平面PAD内的两条相交直线，由此得DC⊥面PAD.

又DC在面PCD上，故面PAD⊥面PCD.

（Ⅱ）解：因

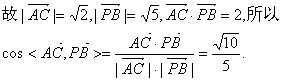
由此得AC与PB所成的角为

（Ⅲ）解：在MC上取一点N（x，y，z），则存在使

要使

为所求二面角的平面角.

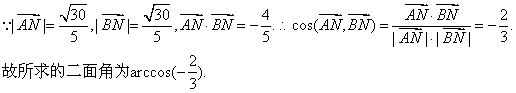
高三数学寒假作业（4）参考答案

1、B　　　　  2、C　　　　3、B　　　　4、②④　　　　5、垂

6、解：（Ⅰ）由  得

即

可得

因为，所以 　解得，因而

 （Ⅱ）因为是首项、公比的等比数列，故

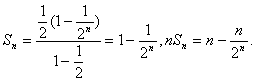
则数列的前n项和

前两式相减，得　

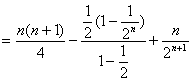　 即　

高三数学寒假作业（5）参考答案

1、D　　　　  2、C　　　　3、 C　　　 4、216　　　　5、①④

6、解法一：　

　　　　　　　　

　　　 由已知得　　

　　　 又　 所以

　　　

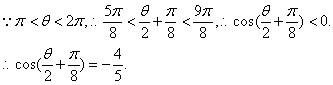
解法二：

　　

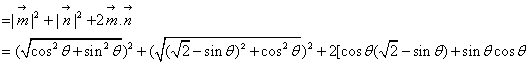
　　　 由已知