高考数学串讲（三） 直线 圆 圆锥曲线
一，基础知识
| 椭圆 | 双曲线 | 抛物线 | |
| 定义 | 与两个定点的距离的 和等于常数 | 与两个定点的距离的 差的绝对值等于常数 | 与一个定点和一条定 直线的距离相等 |
| 标准方程 |
(或 |
(或 |
(或 |
| 参数方程 |
(或 |
(或 |
(或 |
| 焦点 |
|
|
|
| 正数a,b,c, p的关系 |
( |
( | |
| 离心率 |
|
|
|
| 准线 |
|
|
|
| 渐近线 |
| ||
| 焦半径 |
(或
|
(
(点 |
(或 |
| 统一定义 | 到定点的距离与到定 的距离之比等于定值 | 的点的集合 | ,(注:焦点要与对应 准线配对使用) |
),
)
)
)
)
)
或
或
)
)
(或
)
(或
)
(或
)
)
,
),
在左或下支)
)二，跟踪训练
1，（05广东）在平面直角坐标系xOy中，抛物线y=x2上异于坐标原点O的两不同动点A、B满足AO⊥BO（如图4所示）.
（Ⅰ）求△AOB的重心G（即三角形三条中线的交点）的轨迹方程；
（Ⅱ）△AOB的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由.
2，（05广东）在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合（如图5所示）.将矩形折叠，使A点落在线段DC上.
（Ⅰ）若折痕所在直线的斜率为k，试写出折痕所在直线的方程；
（Ⅱ）求折痕的长的最大值.
3,(04全国I)双曲线C：
（
）与直线
：
相交于两个不同
的点A，B．
（I）求双曲线C的离心率
的取值范围；
（II）设直线与
轴的交点为P，且
，求
的值。
4，（05重庆）已知椭圆
的方程为
，双曲线
的左，右焦点分别为的左，右顶点，而的左，右顶点分别是的左，右焦点。
（I）求双曲线的方程；
（II）若直线：
与椭圆及双曲线都恒有两个不同的交点，且与
的两个交点A和B满足
（其中O为原点），求
的取值范围。
5，（04广东）设直线与椭圆
相交于A，B两点，又与双曲线
相交于C，D两点，C，D三等分线段AB。求直线的方程。
三，简明提示
1，（I）设
，则消去
得
；
（II）
，当
，即
时，等号成立。
2，解：设点
落在
上的点
处，则折痕所在的直线是线段
的垂直平分线
(Ⅰ) 的方程为：
①
点的纵坐标恒为1，代入 ①
得点横坐标为
，由：
，得
折痕的方程为：
得：
（其中）②
(II) 若折痕所在直线与轴的交点的纵坐标大于1，则折痕与线段CD有交点
若折痕所在直线与直线
的交点的纵坐标小于0，则折痕与线段AB有交点
对于折痕上的点（
，）
当
时，令
，得：
，又，所以
即：当时，折痕与线段AD有交点 ③
当
时，折痕与线段DC有交点 ④
当时，令，得
，又，所以
即：当时，折痕与BC的边有交点 ⑤
当
时，折痕与线段AB有交点 ⑥
综合③、④、⑤、⑥。记折痕的长度为
（1）
当时，折痕的两个端点分别在AD、BC上
当
时，有最大值
= 
（2）
当
时，折痕的两个端点分别在AB、AD上
设
，
，则
（
）
对
求导数，则：
解
，得
（舍去）或
，而
因此：的最大值
从而得到：
（3）
当时，折痕的两个端点分别在AB、CD上
当
时，有最大值
综合（1）、（2）、（3），得，当时，有最大值。
3，（I）由
，得
①，有
且
，
，得的取值范围为
；
（II）设
，由，得
，
有
，得
，
，消去
，得
。
4，（I）设所求的方程为
，则
，有
；
（II）由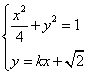
有两个不同解得
①，由
有两个不同解得
且
②，由得
，即
或
③
由①，②，③得的取值范围是
。
5，解：首先讨论l不与x轴垂直时的情况，设直线l的方程为
y=kx+b，如图所示，l与椭圆、双曲线的交点为：
依题意有
，由
得
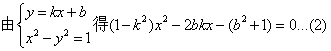
若
，则与双曲线最多只有一个交点，不合题意，故
由
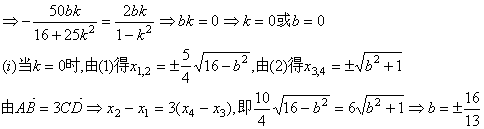
故l的方程为
(ii)当b=0时，由(1)得
故l的方程为
再讨论l与x轴垂直的情况.
设直线l的方程为x=c,分别代入椭圆和双曲线方程可解得，
，
，
综上所述，故l的方程为、和
。