高考数学串讲(六) 高考解题三引
在高考解题时,若能恰到好处地引入一些有力的工具,会对解题带来很大的帮助.下面
我们来探讨一下几种常用解题工具的引入.
一,引入函数
函数是联系运动与静止,变化与定值的有力工具.解题时,若能恰到好处地引入她,会对
我们的解题工作带来很大的帮助.
问题1,(2005全国Ⅲ)若![]() ,
,![]() ,
,![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
问题2,若实数![]() 满足
满足![]() ;
;![]() .求证:
.求证:![]()
![]() .
.
问题3,(2005华师附中测试题)已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求证:
,求证:![]() .
.
(Ⅱ)是否存在实数![]() ,使方程
,使方程![]() 有四个不同的实根?若若存在,求出
有四个不同的实根?若若存在,求出
![]() 的取值范围;若不存在,说明理由.设质
的取值范围;若不存在,说明理由.设质
解答:
问题1,解析:由题之模型,我们引入函数![]() ,可得
,可得![]() .
.
有(1)当![]() 时,
时,![]() ,
,![]() 为增函数;(2)当
为增函数;(2)当![]() 时,
时,![]() ,
,![]() 为减函数.
为减函数.
于是得![]() ,删除A,D又
,删除A,D又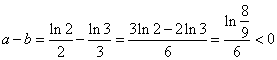 ,知
,知![]() ,于是选C.
,于是选C.
问题2,分析:将所证的不等式作差变形得![]() ,由
,由![]() ,
,
我们设![]() ,这样引入了函数
,这样引入了函数![]() ,现考虑它的单调性即可.
,现考虑它的单调性即可.
解:由![]() ;
;![]() .设
.设![]() ,引入函数
,引入函数
![]() ,可得
,可得![]() .
.
而![]() ,得
,得![]() ,
,![]() ,得
,得![]()
![]() 0.(在
0.(在![]() 时取等号)
时取等号)
所以![]() 在
在![]() 上为减函数,得
上为减函数,得![]() =1,
=1,
即![]() ,于是得
,于是得![]() .
.
问题3,解:(Ⅰ)令![]() .
.
则![]() =
=![]()
由![]() ,得
,得![]() ,知
,知![]() 在
在![]() 上为增函数.
上为增函数.
又![]() 在
在![]() 处连续,得
处连续,得![]() 在
在![]() 上为增函数,
上为增函数,
而![]() ,得
,得![]() =0,即
=0,即![]() .
.
(Ⅱ)由原方程得![]() ①,令
①,令![]() ,并变形得
,并变形得![]() ②
②
要方程①有四个不同实根,则要方程②有两个不同正根.
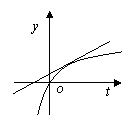 令
令![]() ,
,![]() 它们的图象如右图所示
它们的图象如右图所示
当两曲线在点![]() =
=![]() 处相切时,由
处相切时,由![]() ,
,
得![]() ,于是
,于是![]() ,得切点为
,得切点为![]() ,这时
,这时
切线方程为![]() ,即
,即![]() ,
,
与![]() 轴的交点为
轴的交点为![]() ,要两曲线在
,要两曲线在![]() 轴右边有两个不同交点,
轴右边有两个不同交点,
则![]() ,即
,即![]() .
.
所以当![]() 时,原方程有四个不同的实根.
时,原方程有四个不同的实根.
评注:本题在解答过程中,3处引入了函数,从而为问题的解决带来了方便.
二,引入直角坐标系
直角坐标系实现了数与形之间的真沟通.引入她,可使我们的解题工作左右逢源.
问题4.(2005山东)设![]() 满足约束条件
满足约束条件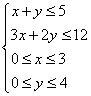 ,则使得目标函数
,则使得目标函数![]() 的值最大的点(
的值最大的点(![]() )是
.
)是
.
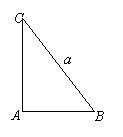 问题5.(2004湖北)如图,在
问题5.(2004湖北)如图,在![]() 中,已知
中,已知![]() .若长为
.若长为![]()
的线段![]() 以点A为中点,问
以点A为中点,问![]() 与
与![]() 的夹角
的夹角![]() 取何值时
取何值时
![]() 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
问题6.(2005天津)某人在山坡P处观看对面山崖顶上的一座铁塔,如图所示,塔高BC=80
(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线![]() ,且点P在直
,且点P在直
线![]() 上,
上,![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,
,![]() .试问,此人距水平地面多远时,观看塔的视角
.试问,此人距水平地面多远时,观看塔的视角
![]() 最大(不计此人的身高)?
最大(不计此人的身高)?

问题7,(05重庆) 如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,EA⊥EB1,已知AB=![]() ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=![]() ,求:
,求:
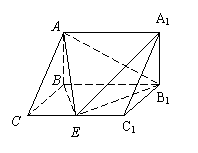 (Ⅰ)异面直线AB与EB1的距离;
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
解答;
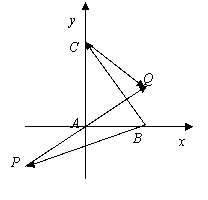 问题4,(2,3) 引入平面直角坐,解决线性规划问题.
问题4,(2,3) 引入平面直角坐,解决线性规划问题.
问题5,解:如图,建立平面直角坐标系,设![]() ,
,
![]() ,则A(0,0),B(
,则A(0,0),B(![]() ,
,![]() .且
.且![]() ,
,
![]() . 设点
. 设点![]() ,则
,则![]() .
.
由![]() ,
,
![]() ,
,![]() .
.
得![]() =
=![]() .
.
又 ,得
,得![]() .于是
.于是![]() .
.
故当![]() ,即
,即![]() (
(![]() 与
与![]() 同向)时,
同向)时,![]() 最大,其最大值为0.
最大,其最大值为0.
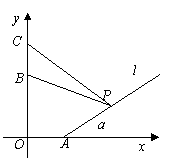 问题6,解:如图所示,建立平面直角坐标系,则A(200,0)
问题6,解:如图所示,建立平面直角坐标系,则A(200,0)
B(0,220),C(0,300).
直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
设点![]() ,则
,则![]()
![]() .
.
由经过两点的直线的斜率公式得
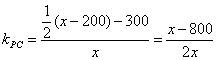 ,
,
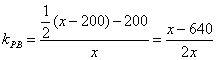 .又由直线PC到直线PB的角的公式得
.又由直线PC到直线PB的角的公式得
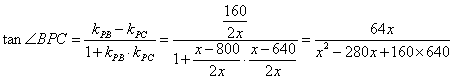
=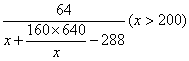 .
.
要使![]() 达到最大,只须
达到最大,只须![]() 达到最小.由均值不等式得
达到最小.由均值不等式得
![]() .
.
当且仅当![]() 时,上式取得等号,故当
时,上式取得等号,故当![]() 时,
时,![]() 最大.
最大.
这时,点P的纵坐标![]() 为
为![]() .由此实际问题知,
.由此实际问题知,![]() ,
,
所以![]() 最大时,
最大时,![]() 最大.
最大.
故当此人距水平地面60米高时,观看铁塔的视角![]() 最大.
最大.
问题7,解:(I)以B为原点,![]() 、
、![]() 分别为y、z轴建立空间直角坐标系.
分别为y、z轴建立空间直角坐标系.
|
在三棱柱ABC—A1B1C1中有
B(0,0,0),A(0,0,![]() ),B1(0,2,0),
),B1(0,2,0),
![]()
设![]()
![]()
![]()
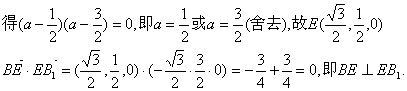
又AB⊥面BCC1B1,故AB⊥BE. 因此BE是异面直线AB、EB1的公垂线,
则![]() ,故异面直线AB、EB1的距离为1.
,故异面直线AB、EB1的距离为1.
(II)由已知有![]() 故二面角A—EB1—A1的平面角
故二面角A—EB1—A1的平面角![]() 的大小为向量
的大小为向量![]() 的夹角.
的夹角.![]()
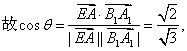
![]()
三,引入向量
向量既有方向,又有大小.她是研究现代数学的有力工具.在解高考题时,我们若能引入她,可使解题工作妙不可言.
问题8, 若异面直线![]() 所成的角为
所成的角为![]() ,AB是公垂线,E,F分别是异面直线
,AB是公垂线,E,F分别是异面直线![]() 上到A,B距离为2和1的两点,当
上到A,B距离为2和1的两点,当![]() 时,线段AB的长为
.
时,线段AB的长为
.
问题9, 已知![]() 都是正数,
都是正数,![]() 且
且![]() ,
,![]() ,则函数
,则函数![]() 的最小值是
.
的最小值是
.

问题10,(04广东)如图,在长方体ABCD—A1B1C1D1中,
已知AB= 4, AD =3, AA1= 2. E、F分别是线段
AB、BC上的点,且EB= FB=1.
(I) 求二面角C—DE—C1的正切值;
(II) 求直线EC1与FD1所成的余弦值.
解答
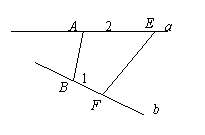 问题8,解:如图, 由
问题8,解:如图, 由![]() ,得
,得
![]()
(1)当![]() 时,有
时,有![]() ,
,
得![]() ;
;
(2)当![]() 时,有
时,有![]() ,得
,得![]() .
.
问题9,由已知,我们作向量![]() ,则
,则![]() ,
,
![]() ,
,![]() .
.
又![]() ,得
,得![]() .
.
即![]() ,于是所求的最小值为1.
,于是所求的最小值为1.
 问题10,解: (I)以A为原点,
问题10,解: (I)以A为原点,![]()
分别为x轴, y轴,z轴的正向建立空间直角坐标系,
则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2)
于是,![]()
设向量![]() 与平面C1DE垂直,则有
与平面C1DE垂直,则有

(II)设EC1与FD1所成角为β,则
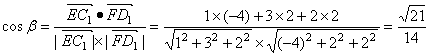 .
.