九年级数学函数练习测试题
第Ⅰ卷(选择题，共50分)
一、选择题 (本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的,请将正确答案代号填在下面的答题框内.)
1．函数y=
的定义域是
( )
A.x≥1＋
或x≤1－
B.－1<x<3
C.1＋≤x<3或－1<x≤1－
D.1－≤x≤1＋
2．若函数y=(
a) x在R上为减函数，则a的取值范围是
( )
A.(0，
) B.(，1) C.(，+∞) D.(1，+∞)
3．已知正实数x1,x2及函数f(x),满足4x=
,且f(x1)+f(x2)=1,则f(x1+x2)的最小值( )
A.4
B.2
C. 
D.
4．下列函数中既是奇函数，又在区间［－1，1］上单调递减的是
A.f(x)= sinx B.f(x)=－x+1
C.f(x)=(ax+a－x)
D.f(x)=ln
5．若函数y=()x+m的图象与x轴有公共点，则m的取值范围是
A.m≤－1 B.－1≤m<0 C.m≥1 D.0<m≤1
6．函数y=loga x在x∈［2，+∞］上总有y>1，则a的取值范围是
A.0<a<或1<a<2
B.<a<1或1<a<2
C.1<a<2
D.0<a<或a>2
7．已知f(x)=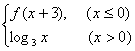
,则f(－9)等于
（ ）
A.－1 B.0 C.1 D.3
8．定义在R上的偶函数f(x)满足对任意x∈R，都有f(x+8)=f(x)+f(4)，且x∈［0，4］时f(x)=4－x，则f(2005)的值为
A.－1 B.1 C.－2 D.0
9．一个人以6米/秒的速度去追停在交通灯前的汽车，当他离汽车25米时，交通灯由红变绿，汽车以1米/秒2的加速度匀加速开走，那么 （ ）
A.人可在7秒内追上汽车 B.人可在10秒内追上汽车
C.人追不上汽车，其间距离最近为5米 D.人追不上汽车，其间距离最近为7米
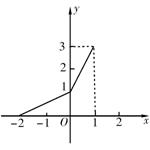
10．在同一平面直角坐标系中，函数y=f(x)和y=g(x)的图象关于直线y=x对称.现将y=g(x)的图象沿x轴向左平移2个单位，再沿y轴向上平移1个单位，所得的图象是由两条线段组成的折线（如图所示），则函数f(x)的表达式为
A.f(x)=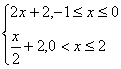
B.f(x)=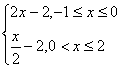 
C.f(x)=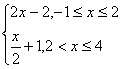 
D.f(x)=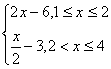 
第Ⅱ卷（非选择题，共70分）
二、填空题 (本大题共4小题，每小题3分，共12分.把答案填在下面的横线上.)
11．已知f(x)是定义在实数集R上的函数，且满足f(x+2)－f(x+2)f(x)－f(x)=1,f(1)=,f(2)=－,则f(2006)=
.
12．若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x2、值域为{1,4}的“同族函数”共有 个.
13． (创新题)规定记号“
”表示一种运算，即ab=
+a+b(a,b为正实数)，若1k=3，则k的值为 ；函数f(x)=kx的值域为
.
14． (创新题)对于函数f(x)定义域中任意x1,x2(x1≠x2)有如下结论：
①f(x1+x2)=f(x1)+f(x2); ②f(x1·x2)=f(x1)+f(x2);
③
；
④f(
)<
.
当f(x)=lgx时，上述结论中正确结论的序号是 .
三、解答题 (本大题6小题，满分58分，解答应写出文字说明、证明过程或演算步骤.)
15．（本小题满分10分）
已知函数f(x)＝a＋
(a，b为实常数).
(Ⅰ)若a＝2，b＝－1，求f(x)的值域．
(Ⅱ)若f(x)的值域为［0，＋∞］，求常数a，b应满足的条件．
16．（本小题满分12分）
某银行准备新设一种定期存款业务，经预测，存款量与存款利率成正比，比例系数为k(k>0)，贷款的利率为4.8%,假设银行吸收的存款能全部放贷出去.
(Ⅰ）若存款利率为x,x∈（0，0.048)，试写出存款数量g(x)及银行应支付给储户的利息h(x)与存款利率x之间的关系式；
（Ⅱ）问存款利率为多少时，银行可获得最大收益？
17．（本小题满分12分）
(甲)设函数f(x)在(－∞，+∞)上满足f(2－x)=f(2+x),f(7－x)=f(7+x),且在闭区间［0，7］上，只有f(1)=f(3)=0.
(Ⅰ)试判断函数y=f(x)的奇偶性；
(Ⅱ)试求方程f(x)=0在闭合区间［－2005，2005］上的根的个数，并证明你的结论.
(乙)设f(x)是定义在(0,+∞)上的函数，且满足关系f(x)=f(
)lgx+1．
(Ⅰ)求f(x)的解析式；
(Ⅱ)求f(x)有最大值和最小值，并求对应的x的值.
18．（本小题满分12分）
已知函数f(x)=1－.
(1)是否存在实数a,b(a<b),使得函数y=f(x)的定义域和值域都是［a,b］.若存在，求出a,b的值；若不存在，请说明理由；
（2）若存在实数a,b(a<b),使得函数y=f(x)的定义域为［a,b］,值域为［ma,mb］(m≠0).求实数m的取值范围.
19．（本小题满分12分）
若函数y=f(x)是周期为2的偶函数,当x∈［2,3］时,f(x)=x－1,在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间［1,3］上,定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
参考答案
1.C 解0<3+2x－x2≤1即得，也可用特殊值法检验.
2.B
由0<log
a<1得<a<1.
3.C
由4x=得出f(x)= 
.由4x1=
,4x2=
两式相乘，并注意到关系f(x1)+f(x2)=1得
=
=
=1+
≥1+
=9(当f(x1)=f(x2)=时取得等号).于是f(x1+x2)=
=1－
≥1－
=.
4.D 用排除法，A是增函数，B不是奇函数，C是偶函数.
5.B
由m=－()x求值域.
6.B 由f(x)=y=logax的图象可知loga2>1,分a>1与0<a<1求解.
7.C 由题意得f(－9)=f(－9+3)=f(－6)=f(－6+3)=f(－3)=f(－3+3)=f(0)=f(0+3)=f(3)=log33=1,故选C.
点评：本题考查分段函数的运用及其有关计算问题.
8.B 由f(4)=0知周期为8，则f(2005)=f(5)=f(－3)=f(3)=1.
9.D 本题是一道加速行程问题，需要运用物理知识建立数学模型，即通过加速运动建立二次函数关系式.
若经t秒人刚好追上汽车，则S+25=6t,由S=t2,得t2－6t+25=0
t2－12t+50=0.考虑距离差d=(S+25)－6t=t2－6t+25=(t－6)2+7,故当t=6秒时，d有最小值7米，即人与汽车最少相距7米，故选D.
10.A 由图象得函数h(x)=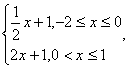
可知g(x)= 
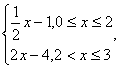再求反函数即得.本题可用特殊值法检验.
11．4 由f(x+2)－f(x+2)f(x)－f(x)=1得：
f(x+2)=
,又因为f(1)=－,f(2)=－,所以f(3)= 
=
,f(4)= 
=
,f(5)= 
=2,f(6)= 
=4,f(7)= 
=－3,f(8)= 
=－
,f(9)=
=－,f(10)= 
=－.由此推得f(x)是以8为周期的周期函数.所以f(2006)=f(8×250+6)=f(6)=4.
12．9 由题意分析知满足题意的函数的定义域有9种:即{－1,－2},{－1,2},{1,－2},{1,2},{－1,－2,2},{1,－2,2},{－1,1,2},{－1,1,－2},{－1,－2,1,2},所以“同族函数”共有9个.
13．1,［1,+∞］ ∵ab=+a+b(a,b为正实数)，∴1k=
+1+k=3(k为正数)，
求得k=1.函数f(x)=kx=1x=
+1+x,f1(x)=,
则f1(x)在［0，+∞］上为增函数.f2(x)=x+1,则f2(x)在［0，+∞］上也为增函数.
由此可得f(0)=1为最小值，所以f(x)=+1+x的值域为［1，+∞］.
点评：本题考查新定义运算符号问题，由运算关系式写1k=3为含k的关系式，求出k的值.第二个问题利用函数单调性求出f(x)的值域.
14．②③ 由对数函数f(x)=lgx的图象和性质可得.
15．解析：(Ⅰ)∵x2＋2x－1＝(x－1)2－2≥－2，∴
≥0,∴f(x)的值域为
［2，+∞)．
(Ⅱ)当a＝0时，则须x2＋b的最小值≤0，∴b≤0;
当a≠0时，只须a＜0，且x2＋ax＋b＝(x+
)2+b－
的最小值b－＝a2，即4b＝5a2.
∴a＝0，b≤0或a＜0，4b＝5a2.
点评：函数的值域与函数的最值密切相关，因此已知函数的值域，可利用函数的最值来列出限制条件.
16．(Ⅰ)由题意知，存款量g(x)=kx,银行应该支付的利息h(x)=xg(x)=kx2,x∈(0,0.048).
(Ⅱ)设银行可获得收益为y，则y=0.048kx－kx2=－k(x－0.024)2+0.0242k,
当x=0.024时，y有最大值，∴存款利率定为0.024时，银行可获得最大收益.
17．(甲)解析：（Ⅰ）由
f(4－x)=f(14－x)
f(x)=f(x+10),从而知函数y=f(x)的周期为T=10
又f(3)=f(1)=0，而f(7)≠0，f(－3)=f(－3+10)=f(7)≠0，所以f(－3)≠±f(3)
故函数y=f(x)是非奇非偶函数;
(Ⅱ)又f(3)=f(1)=0,f(11)=f(13)=f(－7)=f(－9)=0
故f(x)在［0,10］和［－10,0］上均有有两个解,从而可知函数y=f(x)在［0,2005］上有402
个解,在［－2005，0］上有400个解,所以函数y=f(x)在［－2005,2005］上有802个解.
点评：本题重点考查对抽象函数的性质及综合运用函数性质解题的能力，特别是对函数单调性、周期性、奇偶性的讨论，要结合题目所给的条件把三者联系在一起思考.
(乙)解析：(Ⅰ)f(x)=f()lgx+1
①
以代入得：f()=f(x)lg+1，即f()=－f(x)lgx+1 ②
以②代入①得：f(x)=［－f(x)lgx+1］lgx+1，
整理得：f(x)= 
.
(Ⅱ)令t=lgx,则函数变为：y=
.
去分母得：yt2+y=t+1，整理得：yt2－t+(y－1)=0
∵t∈R，∴Δ=1－4y(y－1)≥0，
解得：
≤y≤
，
所以，当t=
=
=－(
+1)，
即x=
时，ymin=；
当t=lgx=
=－1，即x=
－1时，ymax=.
点评：求抽象函数的解析式，有时要通过以变量换变量，然后通过解方程组求出解析式，有时也可以通过取特殊值来求解析式.
18．(1)不存在实数a,b满足条件.
假设存在实数a,b,使得y=f(x)=1－的定义域和值域都是［a,b］,而y≥0,x≠0,所以应有a>0.又f(x)=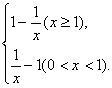
①当a,b∈(0,1)时，f(x)=－1在（0，1）上为减函数，故有
,即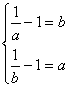
,
由此可推得a=b矛盾，此时实数a,b不存在.
②当a,b∈［1,+∞］时，f(x)=1－=1－在［1，+∞］上是增函数，∴,
即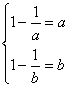
,∴a,b是方程x2－x+1=0的根，但方程x2－x+1=0无实根，所以此时实数a,b也不存在.
③当a∈(0,1),b∈［1,+∞)时，显然，1∈［a,b］,而f(1)=0∈［a,b］,这不可能.此时实数a,b也不存在.
综上可知，适合条件的实数a,b不存在.
(2)若存在实数a,b使函数y=f(x)的定义域为［a,b］,值域为［ma,mb］(m≠0).
由mb>ma， b>a得m(b－a)>0m>0.而ma>0,所以a>0.仿（1）可知，当a,b∈(0,1)或a∈(0,1),b∈［1,+∞］时，a,b不存在.故只可能是a,b∈［1,+∞］.
∵f(x)=1－=1－在区间［1，+∞］上是增函数，
∴
即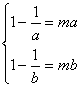
,
∴a,b是方程mx2－x+1=0的两个不等实根，且两实根均大于等于1，∴
解之得0<m<.故实数m的取值范围是(0, ).
19．∵f(x)是以2为周期的周期函数,当x∈［2,3］时,f(x)=x－1,
∴当x∈［0,1］时,f(x)=f(x+2)=(x+2)－1=x+1.
∵f(x)是偶函数,∴当x∈［－1,0］时,f(x)=f(－x)=－x+1,当x∈［1,2］时,f(x)=f(x－2)=－(x－2)+1=－x+3.
设A、B的横坐标分别为3－t,t+1,1≤t≤2,则AB=(t+1)－(3－t)=2t－2,∴△ABC的面积为S=(2t－2)·(a－t)=－t2+(a+1)t－a(1≤t≤2)=－(t－
)2+
∵2<a<3,∴
<<2.当t=时,S最大值=