高考数学复习向量练习试题
第Ⅰ卷(选择题，共40分)
一、选择题 (本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的,请将正确答案代号填在下面的答题框内.)
1.在边长为1的等边△ABC中，若
=a，
=b，
=c，则a·b+b·c+c·a等于
A.
B .-
C.3
D.0
2.已知
=(x+
，y)，
=(x -，y)，且+=6，则2x-3y-12的最大值为
A.12+6
B.12-6
C.6
D.12
3．下列五个命题：
(1)所有的单位向量相等；
(2)长度不等且方向相反的两个向量不一定是共线向量；
(3)若a、b满足a>b且a、b同向，则a>b;
(4)由于零向量的方向不确定，故0与任何向量不平行；
(5)对于任何向量a、b，必有 a +b≤ a +b.
其中正确命题的序号为
A.(1)，(2)，(3) B.(5) C.(3)，(5) A.(1)，(5)
4．已知向量a与b的夹角为
，如果向量2 a +k b与3
a -2b共线，则实数的k的值为
A.
B.-
C. 
D.-
5.设四边形ABCD中，有
=
，且
=，则这个四边形是
A.平行四边形 B.矩形 C.等腰梯形 D.菱形
6．在△ABC中G为边BC中线AH上一点，若AH=2，则
·(
+
)的
A.最大值为-2 B.最大值为2
C.最小值为-2 D.最小值为2
7．已知P1(2，-1)，P2(0，5)，且点P在
的延长线上，
=2
，则点P的坐标为
A.(-2，11) B.(，3) C.(，3) D.(2，-7)
8.已知△ABC三顶点A，B，C的坐标分别为（a1，a2），(b1，b2)，(c1，c2)，在边BC、CA、AB上分别取D、E、F使之满足：
∶=
∶
=
∶
=m∶n，则
A.△DEF与△ABC的重心重合 B.△DEF与△ABC的外心重合
C.△DEF与△ABC的内心重合 D.△DEF与△ABC的垂心重合
第Ⅱ卷(非选择题，共60分)
二、填空题 (本大题共4小题，每小题3分，共12分.把答案填在下面的横线上.)
9.已知点M是△ABC的重心，则
+
+
=
.
10.已知点A(1，-2)，若向量与a ={2，3}同向， =2
，则点B的坐标为
.
11．已知△ABC中，a=x，b=2，B=45°，若该三角形有两个解，则x的取值范围是 .
12.已知a =(cosα，sinα)，b=(cosβ，sinβ)(0<α<β<π)，且λa+μb=μa-λb(λμ≠0)，则β-α= .
三、解答题 (本大题4小题，共48分.解答应写出必要的文字说明、证明过程或演算步骤.)
13. (本小题满分12分)
设e1，e2是两个垂直的单位向量，且a= -(2 e1 + e2)，b= e1-λe2.
(1)若a∥b，求λ的值；（2）若a⊥b，求λ的值.
14.(本小题满分12分)
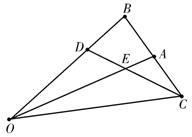如图，在△OAB中，点C是以A为中心的点B的对称点，点D是将
分成2∶1的一个内分点，DC和OA交于点E，设
=a，=b.
（1）用a和b表示向量
、；
（2）若
=λ，求实数λ的值.
15.(本小题满分12分)
(1)已知a=4，b=3，(2a-3b)·(2a+b)=61，求a与b的夹角θ;
(2) =(2，5)，=(3，1)，=(6，3)，在上是否存在点M，使⊥，若存在，求出点M的坐标，若不存在，请说明理由.
16.(本小题满分14分)
已知点H（-3，0），点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足
·
=0，= -
.
（Ⅰ）当点P在y轴上移动时，求点M的轨迹C；
（Ⅱ）过点T（-1，0）作直线l与轨迹C交于A、B两点，若在x轴上存在一点E(x0，0)，使得△ABE是等边三角形，求x0的值.
参考答案
1.B 依题意，得a·b+b·c +c·a=3a2·cos120°= -，选B.
2.A 显然有P(x，y)，A(-，0)，B(，0).由 +=6知，动点P的轨迹为以A（-，0），B（，0）为焦点，长轴长为6的椭圆，其方程为
+
=1，令x=
3cosθ，y=2sinθ，则2x-3y-12=6cos(θ+
)-12，当cos(θ+)=-1时2x-3y-12取最大值为12+6.
3.B 单位向量可能方向不同，所以不一定相等，（1）不正确；只要方向相同或相反的向
量都是共线向量，（2）不正确；向量是不能比较大小的，（3）不正确；按人教版课本规定零向量与任意向量是平行向量，(4)不正确；(5)中为向量模的不等式，正确，故选B.
4.B 2a+k b与3a-2b共线，存在实数t，使2a+k b=
t(3a-2b)，∵a与b的夹角为，则a与b不共线.
∴2=3t，k=
-2t，解得k= -，选B.
点评：本题考查向量的夹角的概念、夹角的求法、向量共线的条件.利用方程思想是求参数的主要方法.
5.C∵=，∴∥且≠，即四边形ABCD为梯形，又= ，∴四边形ABCD为等腰梯形.
6.C·(+)=·(
+
+
+)=2·= -2·≥-2(
)2= -2，故选C.
7.A由定比分点公式可求得P(-2，11)，选A.
8.A由题意有=
，即点D分有向线段所成的比为λ=，设点D的坐标为（x，y)，则由定比分点坐标公式有
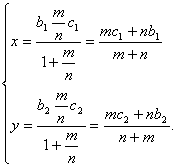
∴D(
，
).
同理可求E（
，
），F(
，
).
设△DEF的重心坐标为（x′，y′），则由重心坐标公式有：
=
(
++)= (a1+b1+c1)，
同理可求y′=(a2+b2+c2)，这也是△ABC的重心坐标.
故△DEF的重心与△ABC的重心重合.
点评：由重心坐标公式，只要求出△DEF的各个顶点坐标即可.三角形的五心中，有四个心在高考中经常出现，需要特别加以关注.一是重心，即各边的中线交点，其重心坐标公式为：x=
，y=
，(其中(x1，y1)，(x2，y2)，(x3，y3)是三角形的三个顶点的坐标）重心分对应的中线所成的比为1∶2的关系.二是外心，即外接圆圆心，也就是中垂线的交点，外心到三个顶点的距离相等.三是内心，即内切圆圆心，也就是角平分线的交点，内心到三边的距离相等.四是垂心，即三角形的三条高的交点.
9．解：设D为AB的中点，则+=2
，又M为△ABC的重心，则= -2，所以++=0.
10.解：设B(x，y)，则=(x-1，y+2)，与同a同向，∴3(x-1)=2(y+2)，又AB=
=2，解得x=5，y=4或x= -3，y=
-8，而当x=
-3，y= -8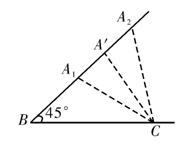
时，与a反向，故B为(5，4).
11.（2，2） 如图，当A ′C=2时，
三角形有且只有一解，此时BC=2，∴x<2.
又∵三角形有两解，∴x>2，综合得x∈(2，2).
12.解：∵λ a+μ b=(λcosα+μcosβ，λsinα+μsinβ)=
，
同理μa-λb=，由λa+μb=μa-λb得cos(β-α)=0.
∵0<α<β<π，∴β-α=
.
13.解：（1）∵a∥b，∴a=mb，即-2e1- e2=m e1 -mλe2
∴
解得：m=
-2，λ= -.
(2)∵a⊥b，∴a·b=0，(-2e1- e2)·(e1-λe2)=0
即 -2 e12+2λe1·e2- e2·e1+λe22=0，-2 +λ=0，∴λ=2.
点评：本题考查两个向量垂直、平行的充要条件、向量的数量积的意义.
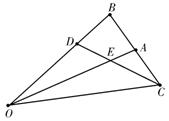14.解：（1）依题意，A为BC中点，则2=+.
=2-=2a-b ∴=-
=-=2 a-b-b=2 a-
b.
（2）若=λ，则=-=λ a-(2a-b)=(λ-2)a+b.
∵与共线，∴存在实数k，使=k.
∴(λ-2)a+b=k(2a-b) ∴解得λ=
.
15.(1)∵ (2a-3b)·(2a+b)=61，∴4a2-4a·b-3b2=61.
又a=4，b=3，∴4×16-4a·b-3×9=61，
∴a·b= -6，∴cosθ=
= -，∴θ=120°.
(2)设存在点M，且
=λ
=(6λ，3λ)(0<λ≤1)，∴
=(2-6λ，5-3λ)，
=(3-6λ，1-3λ).
∴45λ2-48λ+11=0，解得：λ=或λ=
，∴=(2，1)或 =(
，)满足题意.∴存在M（2，1）或M（，）满足题意.
16．解（Ⅰ）设点M的坐标为(x，y)，则= -，得P(0，-
)，Q(
，0)，由·=0，
得(3，-)·(x，
)=0，所以y2=4x，由点Q在x轴的正半轴上，得x>0，所以，动点M的轨迹C是以(0，0)为顶点，以(1，0)为焦点的抛物线，除去原点.
（Ⅱ）设直线l：y=k(x+1)，其中k≠0代入y2=4x，
得k2x2+2(k2-2)x+k2=0，(1)
设A(x1，y1)，B(x2，y2)，则x1，x2是方程(1)的两个实数根，由韦达定理得
x1+x2=
-
，
所以，线段AB的中点N坐标为(
，
)，
线段AB的垂直平分线方程为y -= -
(x -)，
令y=0，x0=
+1，所以，点E的坐标为(+1，0).
因为△ABE为正三角形，所以，点E(+1，0)到直线AB的距离等于
AB，而AB=
=
·
，NE=
，∴
=，解得k=±，所以，x0=
.