高考文科数学2月统一考试试题
数学(文史类)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第l卷1至2页,第Ⅱ卷3至8页,共150分,测试时间120分钟.
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.
2.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案,不能答在测试卷上.
一、选择题:本大题共12个小题.每小题5分;共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.![]() 的共轭复数是
的共轭复数是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知:![]() ,若
,若![]() 同时为假命题,则满足条件的
同时为假命题,则满足条件的![]() 的集合为
的集合为
A.![]() 或
或![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]()
4.已知函数![]() ,给出以下四个命题,其中为真命题的是
,给出以下四个命题,其中为真命题的是
A.若![]() ,则
,则![]()
B.在区间![]() 上是增函数
上是增函数
C.直线![]() 是函数图象的一条对称轴
是函数图象的一条对称轴
D.函数的图象可由![]() 的图象向右平移
的图象向右平移![]() 个单位得到
个单位得到
5.已知![]() 与
与![]() 为互相垂直的单位向量,
为互相垂直的单位向量,![]() ,
,![]() 且
且![]() 与
与![]() 的夹角为锐角,则实数
的夹角为锐角,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.若![]() 表示直线,
表示直线,![]() 表示平面,则
表示平面,则![]() 的一个充分条件是
的一个充分条件是
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]() ,则
,则![]()
7.甲乙两人随意入住两间空房,则甲、乙两人各住一间房的概率是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.函数![]() 与
与![]() 在同一直角坐标系下的图象大致是
在同一直角坐标系下的图象大致是
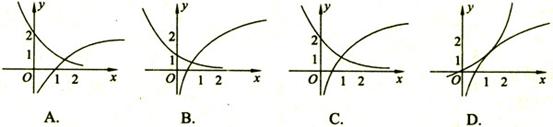
9.设数列![]() 是等差数列,且
是等差数列,且![]() 是数列
是数列![]() 的前
的前![]() 项和,则
项和,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知圆![]() 及直线
及直线![]() ,当直线
,当直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() 时,则
时,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知![]() ,则
,则![]() 之间的大小关系为
之间的大小关系为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.设![]() 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当![]() 时,
时,![]() ,若对任意的
,若对任意的![]() ,不等式
,不等式![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
注意事项:
1.第Ⅱ卷共6页,用钢笔或蓝圆珠笔直接写在试卷中.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共4个小题.每小题4分,共16分.把答案填在题中横线上.
13.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为2,2,3,则此球的表面积为 .
 14.不等式组
14.不等式组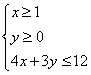 表示的平面区域的面积为
.
表示的平面区域的面积为
.
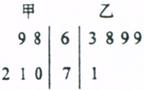
15.甲、乙两位同学某学科的连续五次考试成绩用茎叶图表示如图,则平均分数较高的是 ,成绩较为稳定的是 。
16.已知双曲线![]() 的一条渐近线方程为
的一条渐近线方程为![]() ,则该双曲线的离心率
,则该双曲线的离心率![]() 为
.
为
.
三、解答题:本大题共6个小题,共74分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)
设向量![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() ;
;
(2)求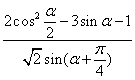 .
.
18.(本小题满分12分)
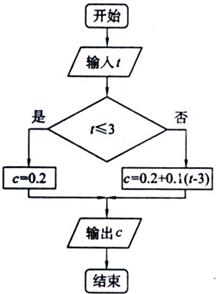
某市电信部门规定:拨打本市电话时,如果通话时间不超过3分钟,则收取通话费0.2元;如果通话时间超过3分钟,则超过部分以0.1元/分钟收取通话费(时间以分钟计,不足1分钟按1分钟计)。现设计了一个计算通话费用的算法:
S1 输入通话时间![]() (
(![]() 按题目要求取整数);
按题目要求取整数);
S2 如果![]() ,则
,则![]() ,否则
,否则![]() ;
;
S3 输出费用![]()
(1)试写出该算法的一个程序框图;
(2)表1为A、B、C、D、E五人拨打本市电话的情况,将A、C的应缴话费数填入表1中适当位置;
表1
| A | B | C | D | E | |
| 第一次通话时间 | 3分钟 | 3分45秒 | 3分55秒 | 3分20秒 | 6分钟 |
| 第二次通话时间 | 0分钟 | 4分钟 | 3分40秒 | 4分50秒 | 0分钟 |
| 第三次通话时间 | 0分钟 | 0分钟 | 5分钟 | 2分钟 | 0分钟 |
| 应缴话费(元) | 0.60 | 0.90 | 0.50 |
(3)根据表1完成表2
表2
| 时间段 | 频数 | 频率 | 累积频率 |
|
| 2 | 0.2 | 0.2 |
|
| |||
|
| |||
|
| |||
| 合计 | 10 | 1 | 1 |
19.(本小题满分12分)
如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
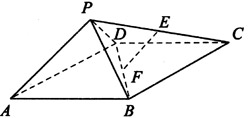 (2)证明:面PDC⊥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
20.(本小题满分12分)
在数列![]() 中,
中,![]() ,
,![]() .
.
(1)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)证明不等式![]() ,对任意
,对任意![]() 皆成立。
皆成立。
21.(本小题满分12分)
已知椭圆![]() 与直线
与直线![]() 相交于两点
相交于两点![]() .
.
(1)当椭圆的半焦距![]() ,且
,且![]() 成等差数列时,求椭圆的方程;
成等差数列时,求椭圆的方程;
(2)在(1)的条件下,求弦![]() 的长度
的长度![]() ;
;
(3)当椭圆的离心率![]() 满足
满足![]() ,且
,且![]() (
(![]() 为坐标原点)时,求椭圆长轴长的取值范围.
为坐标原点)时,求椭圆长轴长的取值范围.
22.(本小题满分14分)
已知定义在正实数集上的函数![]() ,其中
,其中![]() 。设两曲线
。设两曲线![]() 有公共点,且在公共点处的切线相同。
有公共点,且在公共点处的切线相同。
(1)若![]() ,求
,求![]() 的值;
的值;
(2)用![]() 表示
表示![]() ,并求
,并求![]() 的最大值。
的最大值。
数学(文史类)试题参考答案及评分标准
一、
1.D 2.B 3.D 4.C 5.A 6.D 7.C 8.C 9.B 10.C
11.C 12.A
二、
13.![]() 14.
14.![]() 15.甲,甲 16.
15.甲,甲 16.![]() 或
或![]()
三、
17.(1)![]()
![]()
![]() 3分
3分
∴![]() 4分
4分
∴![]() 6分
6分
(2)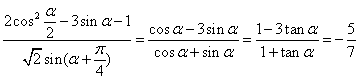 . 12分
. 12分
18.(1)
 5分
5分
(2)0.20 1.00 9分
(3)
| 时间段 | 频数 | 频率 | 累积频率 |
|
| 2 | 0.2 | 0.2 |
|
| 5 | 0.5 | 0.7 |
|
| 2 | 0.2 | 0.9 |
|
| 1 | 0.1 | 1 |
| 合计 | 10 | 1 | 1 |
12分
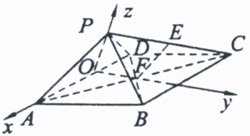 19.(1)如图,连接AC,
19.(1)如图,连接AC,
∵ABCD为矩形且F是BD的中点,
∴AC必经过F 1分
又E是PC的中点,
所以,EF∥AP 2分
∵EF在面PAD外,PA在面内,∴EF∥面PAD 4分
(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD![]() 面ABCD=AD,∴CD⊥面PAD,
面ABCD=AD,∴CD⊥面PAD,
又AP![]() 面PAD,∴AP⊥CD 6分
面PAD,∴AP⊥CD 6分
又∵AP⊥PD,PD和CD是相交直线,AP⊥面PCD 7分
又AD![]() 面PAD,所以,面PDC⊥面PAD 8分
面PAD,所以,面PDC⊥面PAD 8分
(3)取AD中点为O,连接PO,
因为面PAD⊥面ABCD及△PAD为等腰直角三角形,所以PO⊥面ABCD,
即PO为四棱锥P—ABCD的高 10分
∵AD=2,∴PO=1,所以四棱锥P—ABCD的体积![]()
12分
20.(1)数列![]() 的通项公式为
的通项公式为![]()
所以数列![]() 的前
的前![]() 项和
项和![]() 4分
4分
(2)任意![]() ,
,![]()
![]() 8分
8分
当![]() 时,
时,![]() ;
;
当![]() 且
且![]() 时,
时,![]() ,∴
,∴![]() ,即
,即![]()
所以不等式![]() ,对任意
,对任意![]() 皆成立。 12分
皆成立。 12分
21.(1)由已知得:![]() ,∴
,∴![]() 2分
2分
所以椭圆方程为:![]() 3分
3分
(2)![]() ,由
,由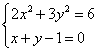 ,得
,得![]() 5分
5分
∴![]() 6分
6分
∴![]() 7分
7分
(3)由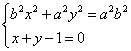 ,得
,得![]()
由![]() ,得
,得![]()
此时![]() 8分
8分
由![]() ,得
,得![]() ,∴
,∴![]()
即![]() ,故
,故![]()
由![]() ,得
,得![]()
∴![]()
由![]() 得
得![]() ,∴
,∴![]()
所以椭圆长轴长的取值范围为![]() 12分
12分
22.(1)设![]() 与
与![]() 在公共点
在公共点![]() 处的切线相同
处的切线相同
![]() 2分
2分
由题意知![]() ,∴
,∴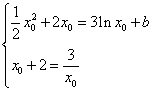 4分
4分
由![]() 得,
得,![]() ,或
,或![]() (舍去)
(舍去)
即有![]() 6分
6分
(2)设![]() 与
与![]() 在公共点
在公共点![]() 处的切线相同
处的切线相同
![]()
由题意知![]() ,∴
,∴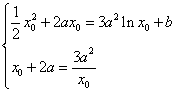
由![]() 得,
得,![]() ,或
,或![]() (舍去) 9分
(舍去) 9分
即有![]() 10分
10分
令![]() ,则
,则![]() ,于是
,于是
当![]() ,即
,即![]() 时,
时,![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() 13分
13分
故![]() 在
在![]() 的最大值为
的最大值为![]() ,故
,故![]() 的最大值为
的最大值为![]() 14分
14分
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
|
|
| ||||||||||||||||
| ||||||||||||||||
| ||||||||||||||||