当前位置：首页 -高中数学试卷 - 高考数学试题 - 正文*

高考数学复习—圆锥曲线练习试卷

2014-5-11 0:13:04下载本试卷

高考数学复习—圆锥曲线练习试卷

第Ⅰ卷　(选择题　共50分)

一、选择题(10×5′=50′)

第1题图
 
1.已知有向线段的起点P（-1，1），终点Q（2，2）,

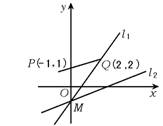
若直线l:x+my+m=0与有向线段的延长线相交，如图所示，

则m的取值范围是　　(　　)

A.　　　　　　　　　 B.

C.(-∞,-3) 　　　　　　　　　 D.

2.若P(x1,y1)是直线l:f (x,y)=0上的一点,Q(x2,y2)是直线l外一点,则方程f (x,y)=f (x1,y1)+f (x2,y2)表示的直线　　(　　)

A.与l重合　　　　　　　　  B.与l相交于点P

Ｃ.过点Ｑ且与l平行　　　　 Ｄ.过点Q且与l相交

3.直线l:y=kx+1(k≠0)，椭圆E：.若直线l被椭圆E所截弦长为d,则下列直线中被椭圆E所截弦长不是d的直线是　　(　　)

A.kx+y+1=0　　　　　　  B.kx-y-1=0

C.kx+y-1=0　　　　　　　 D.kx+y=0

4.若m、n是不大于6的非负整数，则Cx2+Cy2=1表示不同的椭圆的个数为　　(　　)

A.A　　　　 B.C　　　　C.A　　　　 D.C

5.在椭圆上一点A看两焦点F1、F2的视角为直角，设AF1的延长线交椭圆于点B，又AB=AF2，则椭圆的离心率e可能为　　(　　)

A.2-2　　　　B.　　　　 C.-1　　　 　D.

6.F1、F2分别为椭圆的左、右焦点，AB为其过点F2且斜率为1的弦，则·的值为　  (　　)

A.　　　 B.　　　　C.　　　　  D.5

7.如果把圆C:x2+y2=1沿向量a=(1,m)平移到C′,且C′与直线3x-4y=0相切,则m的值为　(　　)

A.2或-　　  B.2或　　　　C.-2或　　　　D.-2或-

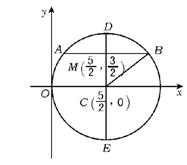
8.在圆x2+y2=5x内,过点有n条弦的长度成等差数列,最小弦长为数列的首项a1,最大弦长为an,若公差d∈,那么n的取值集合为　　(　　)

A.{3,4,5}　　　B.{4,5,6}　　　　C.{3,4,5,6}　　　 D.{4,5,6,7}

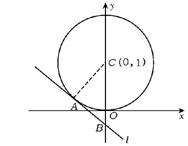
9.若当p(m,n)为圆x2+(y-1)2=1上任意一点时，不等式m+n+c≥0恒成立，则c的取值范围是 (　　)

A.-1-≤c≤-1　　　　  B.-1≤c≤+1

C.c≤--1　　　　　　　　 D.c≥-1

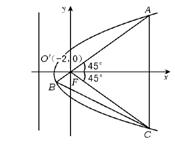
10.过抛物线y2=8(x+2)的焦点F作倾斜角为45°的直线交抛物线于A、B两点，使AF>BF,过点A作与x轴垂直的直线交抛物线于点C,则△BCF的面积是　　(　　)

A.64　　　　B.32　　　　 C.16　　　　D.8

二、填空题（4×4′=16′）

11.一个圆周上有10个点，每两点连成一条弦，这些弦在圆内的交点最多有　　　　 个.

12.设圆C经过点M(-2,0)和点N(9,0),直线l过坐标原点,圆C与直线l相交于点P、Q,当直线l绕原点在坐标平面内旋转时,弦PQ长度的最小值是　　　　  .

13.函数y=的图象是平面上到两定点距离之差的绝对值等于定长的点的轨迹，则这个定长是　　　　　 .

14.椭圆(a>b>0)的两焦点为F1、F2，以F1F2为边作正三角形，若椭圆恰好平分正三角形的另两条边，则椭圆的离心率为　　　　　  .

三、解答题（4×10′+14′=54′）

15.对任意的实数λ,直线(2+λ)x-(1+λ)y-2(3+2λ)=0与点P(-2,2)的距离为d,求d的取值范围.

16.已知椭圆E：(a>b>0),以F1（-c,0）为圆心，以a-c为半径作圆F1，过点B2（0,b）作圆F1的两条切线，设切点为M、N.

(1)若过两个切点M、N的直线恰好经过点B1(0,-b)时，求此椭圆的离心率;

(2)若直线MN的斜率为-1,且原点到直线MN的距离为4（-1）,求此时的椭圆方程；

(3)是否存在椭圆E，使得直线MN的斜率k在区间(-)内取值？若存在，求出椭圆E的离心率e的取值范围；若不存在，请说明理由.

17.椭圆的焦点在y轴上，中心在原点，P为椭圆上一点，F1、F2为椭圆两焦点，点P到两准线的距离分别为和,且PF1⊥PF2.

(1)求椭圆的方程；

(2)过点A（3，0）的直线l与椭圆交于M、N两点，试判断线段MN的中点Q与点B（0，2）的连线能否过椭圆的顶点，若能则求出l的方程，若不能则说明理由.

18.椭圆E的中心在原点O，焦点在x轴上，离心率e=,过点C(-1,0)的直线l交椭圆于A、B两点，且满足：=λ.

(1)若λ为常数,试用直线l的斜率k(k≠0)表示△OAB的面积;

(2)若λ为常数，当△OAB的面积取得最大值时，求椭圆E的方程;

(3)若λ变化，且λ=k2+1,试问：实数λ和直线l的斜率k(k∈R)分别为何值时，椭圆E的短半轴长取得最大值？并求出此时的椭圆方程.

19.有一张矩形纸片ABCD，如图(1)所示那样折叠，使每次折叠后，点A都落在DC边上，试确定：是否存在一条曲线，使这条曲线上的每一点都是某条折痕（满足以上条件）与该曲线的切点，且每条折痕与该曲线相切［如图(2)］.

第19题图
 


圆锥曲线练习参考答案

一、选择题

1.B　易知kPQ=,直线x+my+m=0过点M（0，-1）.

当m=0时，直线化为x=0,一定与PQ相交，所以m≠0.

当m≠0时，k1=-.考虑直线l的两个极限位置.

(1)l经过点Q，即直线为l1,则k=.

(2)l与平行，即直线为l2,则k=kPQ=.

∴<-<.∴-3<m<-.故选B.

2.C　由题意知f (x1,y1)=0,f (x2,y2)=m(m为非零常数).所以方程f (x,y)=f (x1,y2)+f (x2,y2),即f (x,y)-m

=0.所以f (x)表示的直线过点Ｑ,且平行于直线l.

3.D　因为A、B、C三个选项分别是直线l关于x轴、原点、y轴的对称直线，又椭圆E关于x轴、原点、y轴都对称，所以A、B、C三个选项所表示的直线被椭圆E所截弦长都是d.故选D.

4.C　因为C只有4个不同的值，故选C.

5.B　由题意知AF1≠AF2.∴2(AF12+AF22)>(AF1+AF2)2.

∴2×4c2>4a2.∴e=>≈0.707.

对照备选答案，只有B可能.

6.C　分析　本题可把直线AB与椭圆两方程联立求出A、B坐标后写出、的坐标表示，再按定义进行.也可先求出向量、，利用·=(+)·(+)来做.

解法一　消去y得5x2-8x+8=0,

设A(x1,y1),B(x2,y2).

∴·=(x1+,y1)·(x2+,y2)=(x1+,x1-)·(x2+,x2-)

=(x1+)(x2+)+(x1-)(x2-)=2(x1x2+3)=2(+3)=,选C.

解法二　设直线AB方程为,代入椭圆方程,有5t2+2t-2=0

·=(+)·(+)=()2+·(+)+·

=(2)2+2··+=.选C.

7.A　平移后圆的方程为(x-1)2+(y-m)2=1.由题意知平移后所得的圆的圆心到直线的距离d==1,解得m=2或-.

8.D　如图，⊙C的圆心为C(),半径R=CB=,最短弦a1=AB=4,最长弦an=DE=5.

由an=a1+(n-1)d,得d=,已知d∈,

∴n-1∈［3,6］,n∈［4,7］,即n=4,5,6,7.选D.

第8题图解
 

第9题图解
 


9.D　本题是解析几何题型，而又求数的范围,故适合用数形结合思想直观解之.

如图，圆C恒在直线y=-x-c上方，至少直线l与圆相切于A点,若l交y轴于B,

∵kl=-1,∴△ABC为等腰直角三角形.AB=AC=1,BC=,必有B(-+1,0),

即直线的纵截距-c≤-+1时圆恒在直线l上方，∴c≥-1.选D.

第10题图解
 
10.C　分析　如图由抛物线关于x轴对称知∠AFC=90°,

△BFC为Rt△,只须求FB、FC之长即可.

解　抛物线顶点为(-2,0),且焦参数p=4,知焦点F(0,0)为原点.

∴直线AB的方程为y=x,代入抛物线方程:x2=8(x+2).

即(x-4)2=32,∴x=4±4.

故有A(4+4,4+4),B(4-4,4-4),C(4+4,-4-4).

由条件知∠AFx=∠CFx=45°,∴在△BFC中∠BFC=90°.

∴S△BFC=FB·FC=

==32-16=16.∴选C.

二、填空题

11.210　分析　本题直接求解较难，可转化为求圆的内接四边形的个数（由于每一个四边形，对应着对角线的一个交点），从而使问题简化.

解　在圆内相交于一点的两弦，可作为一个四边形的两条对角线，它对应着一个圆内接四边形.反之，每一个圆内接四边形，都对应着对角线的一个交点.这样，圆内接四边形与弦在圆内的交点可建立一一对应的关系.因此，弦在圆内的交点最多有C=210个.

12.6　当直线l绕原点O旋转到使OC垂直于l时,｜PQ｜最小.因为O为PQ的中点,所以由相交弦定理得｜OP｜｜OQ｜=｜OM｜｜ON｜=18,即｜OP｜2=18,所以｜OP｜=3.所以｜PQ｜=2｜OP｜=6.

13.2　由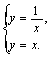得A(-1,-1)、B(1,1)，所以2a=AB=2.

14.-1　设过左焦点F1的正三角形的边交椭圆于点A，则AF1=c,AF2=c.

∴2a=(1+)c.∴e==.

三、解答题

15.解　将原方程化为(2x-y-6)+λ(x-y-4)=0,它表示的是过两直线2x-y-6=0和x-y-4=０交点的直线系方程,但其中不包括直线x-y-4=０.因为没有λ的值使其在直线系中存在.解方程组得所以交点坐标为(2,-2).当所求直线过点Ｐ和交点时,d取最小值为０;当所求直线与过点Ｐ和交点的直线垂直时,d取最大值,此时有d=.

但是此时所求直线方程为x-y-4=0.而这条直线在直线系中不存在.所以d的取值范围是.

16.解　（1）圆F1的方程是（x+c）2+y2=(a-c)2,因为B2M、B2N与该圆切于M、N点，所以B2、M、F1、N四点共圆，且B2F1为直径，则过此四点的圆的方程是(x+)2+(y-)2=,从而两个圆的公共弦MN的方程为cx+by+c2=(a-c)2,又点B1在MN上,

∴a2+b2-2ac=0,∵b2=a2-c2,

∴2a2-2ac-c2=0,即e2+2e-2=0,∴e=-1.(负值已舍去)

(2)由（1）知，MN的方程为cx+by+c2=(a-c)2,由已知-=-1.

∴b=c,而原点到MN的距离为d==2c-a=()a,

∴a=4,b2=c2=8,所求椭圆方程是;

(3)假设这样的椭圆存在，由（2）则有-<-<-,

∴<<,∴<<,∴<<.故得2<<3,

∴3<<4,求得<e<,即当离心率取值范围是（,）时，直线MN的斜率可以在区间(,-)内取值.

17.解　（1）设椭圆的方程为(a>b>0),c=,

PF1=m,PF2=n,则由题意和椭圆的性质得m+n=2a,n=2m,m2+n2=4c2,

解得a=3,b=2,c=.

故所求的椭圆方程为.

(2)由（1）知直线l与椭圆相交时斜率一定存在，故设l的方程为y=k(x-3),

代入,整理得(9+4k2)x2-24k2x+36k2-36=0

由Δ=(-24k2)2-4(9+4k2)(36k2-36)>0,

得-.设M(x1,y1),N(x2,y2),Q(x0,y0)

则x0=,y0=k(x0-3)=-

当k=0时，Q为坐标原点，BQ过椭圆顶点（0，3）和（0，-3），此时l的方程为y=0;

当k≠0时，x0≠0,则直线BQ的方程为y=x+2,

若直线BQ过顶点（2，0），则×2+2=0,即x0+y0=2,

所以=24k2-27k-18=0,

解得k=或k=(舍去)

此时l的方程为y=x+2

若直线BQ过顶点(-2,0),则×(-2)+2=0,即x0-y0=-2,

所以=-220k2+27k+18=0.

方程无实根，直线l不存在

18.解　设椭圆方程为(a>b>0).

由e==及a2=b2+c2得a2=3b2,故椭圆方程为x2+3y2=3b2　　　　①

(1)∵直线l:y=k(x+1)交椭圆于A（x1,y1）,B(x2,y2)两点，并且=λ(λ≥2),

∴(x1+1,y1)=λ(-1-x2,-y2)，即　　　　　　　　  ②

把y=k(x+1)代入椭圆方程，得(3k2+1)x2+6k2x+3k2-3b2=0,且k2(3b2-1)+b2>0,

∴x1+x2=-,　　　　　　　　　　　　　　  ③

x1x2=,　　　　　　　　　　　　　　　  ④

∴S△OAB=×１×y1-y2=λ+1·y2=·k·x2+1.

联立②、③得x2+1=,

∴S△OAB=·(k≠0),

(2)S△OAB=·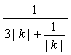≤(λ≥2).

当且仅当3k=,即k=±时，S△OAB取得最大值，

此时，x1+x2=-1,又∵x1+1=-λ(x2+1),

∴x1=,x2=,代入④得3b2=

故此时椭圆的方程为x2+3y2=(λ≥2).

(3)由②、③联立得：x1=,x2=,

将x1、x2代入④，得3b2=.

由k2=λ-1得3b2==+1.

易知，当λ≥2时,3b2是λ的减函数，故当λ=2时，(3b2)max=3.

故当λ=2,k=±1时，椭圆短半轴长取得最大值，此时椭圆方程为x2+3y2=3.

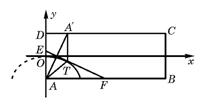
19.解　以AD的中点为原点建立直角坐标系（如图），

第19题图解
 
设AD=p,则点A的坐标为(0,-).A′是DC上任意一点，

EF是A与A′重合时的折痕，易证:EF是AA′的中垂线，

过A′作A′T⊥DC,交EF于T，设T的坐标为(x,y),于是有

A′T=-y,AT=,由TA′=AT,得 (-y)2=

x2+(y+)2,整理得y=-x2,由此可知点T的轨迹为一段抛

物线，下面证明每一条折痕EF与抛物线y=-x2相切于点T，设AA′的斜率为k,则易得k=,

由于EF是AA′的中垂线，所以EF的方程为y=-.

联立直线EF与抛物线的方程：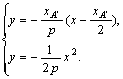

得x2-2xA′·x+x2A′=0,(x-xA′)2=0,解得重根x=xA′,直线EF与抛物线y=-x2相切于点T，故存在一条曲线（抛物线），这条曲线（抛物线）上的每一点都是某条折痕与该曲线的切点，且每条折痕与该曲线相切.