高考数学复习—导数及其应用练习试题卷

高考数学复习—导数及其应用练习试题卷

一、选择题(10×5′=50′)

1.曲线y=x在点P（2，8）处的切线方程为　　(　　)

A.y=6x-12　　　　B.y=12x-16　　　　　 C.y=8x+10　　　　D.y=12x-32

2.过原点与曲线y=相切的切线方程为　  (　　)

A.y=x　　　　 B.y=2x　 　　　C.y=x　　　　  D.y=x

3.物体自由落体运动方程为s=s(t)=gt,g=9.8m/s,若v==g=9.8m/s.那么下列说法正确的是　  (　　)

A.9.8m/s是在1s这段时间内的速率

B.9.8m/s是从1s到（1+Δt）s这段时间内的速率

C.9.8m/s是物体在t=1 s这一时刻的速率

D.9.8m/s是物体从1 s到（1+Δt）s这段时间内的平均速率

4.已知过曲线y=x上点P的切线l的方程为12x-3y=16,那么P点坐标只能为　　(　　)

A.　　　 B.　　　　 C.　　　　  D.

5.一质点做直线运动，若它所经过的路程与时间的关系为：s(t)=4t-3(s单位：m,t单位：s),则t=5时的瞬时速率为　　(　　)

A.37　　　　 B.38　　　　 C.39　　　　  D.40

6.一个圆半径以0.1 cm/s速率增加，那么当半径r=10 cm时，此圆面积的增加速率（单位：cm/s）为　  (　　)

A.3π　　　　  B.4π　　　　　 C.2π　　　　　　 D.π

7.一圆面以10π cm/s的速率增加，那么当圆半径r=20 cm 时，其半径r的增加速率u为 (　　)

A. cm/s　　　　 B. cm/s　　　　 C. cm/s　　　　 D. cm/s

8.曲线y=x(n∈N)在点P(,2)处切线斜率为20，那么n为　　(　　)

A.7　　　　  B.6　　　　C.5　　　　 D.4

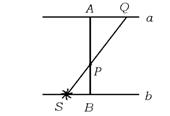
9.直线a∥b，a处一面高墙，点P处站一人，P到直线a的距离PA＝10 m,P到直线b的距离PB＝2 m,在夜晚一光源S从B点向左运动，速率为5 m/s(沿直线b运动)，那么，P点处的人投在墙a上影子Q的运动速率为　　(　　)

A.10 m/s　　　　 B.15 m/s　　　　 C.20 m/s　　　　  D.25 m/s

第10题图

10.质点P在半径为r的圆周上逆时针方向做匀角速率运动，

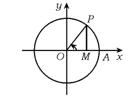
角速率为1 rad/s.如图所示，设A为起点，那么t时刻点P在x

轴上射影点M的速率为　　(　　)

A.rsint　　　　  B.-rsint　　　　 C.rcost　　　　D.-rcost

二、填空题（4×4′=16′）

11.曲线y=x(x+1)(2-x)有两条平行于直线y=x的切线，则两切

线之间的距离是　　　　　 .

12.函数S=esin(ωt+φ),那么S′t为　　　　  .

13.设曲线y=上有点P(x₁,y₁)，与曲线切于点P的切线为m.若直线n过P且与m垂直，则称n为曲线在P处的法线，设n交x轴于Q,又作PR⊥x轴于R,则RQ的长是　　　　 .

14.设坐标平面上的抛物线y=x的图象为C,过第一象限的点(a,a)作C的切线l,则l与y轴的交点Q的坐标为　　　　  ,l与y轴夹角为30°时，a=　　　　　 .

三、解答题（4×10′+14′=54′）

15.A(1,c)为曲线y=x-ax+b上一点，曲线在A点处的切线方程为y=x+d,曲线斜率为1的切线有几条？它们之间的距离是多少？

16.已知抛物线C:y=x+2x和C:y=-x+a，如果直线l同时是C和C的切线，则得l为C1和C的公切线，公切线上两切点之间的线段称为公切线段.

(1)a取什么值时，C和C有且仅有一条公切线?写出此公切线方程；

(2)若C与C有两条公切线，证明相应的两条公切线段互相平分.

17.已知函数f(x)=ln(x+1)-x.

(1)求函数f (x)的单调递减区间;

(2)若x>-1,证明：1-≤ln(x+1)≤x.

第18题图

18.如图所示的是曲柄连杆装置，

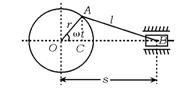
（1）求滑块运动方程；

（2）求滑块运动速率.

19.质点运动方程s=f (t)实为位移s对时间t的函数，质点的运动速度即是对应的位移函数的导数s′=f ′(t).

(1)求质点运动s₁=vt+s₀和s₂=at+vt+s₀的运动速度并判定运动的性质.(v、a、s均为大于零的常数)

(2)已知某质点的运动方程为s=sin2πt,问此运动何时速度为0？

导数练习100分参考答案

一、选择题

1.B　设所求切线斜率为k,那么，k===12,所以，所求切线方程为

y-8=12(x-2),整理得:y=12x-16.

2.A　设切点P（x,），那么切线斜率k=y′=.又因为切线过点O（0，0），及点P，则k=,所以=.

解得x=2.所以斜率k=.从而切线方程为:y=x.

3.C

4.A　设P点坐标为,由导数几何意义可知：y′=k=4,又因为y′=x,

所以x=±2,所以点P 坐标为.

5.D　设物体在时刻5时的瞬时速度为:v(5)= .

6.C　当圆半径变化t s时，圆面积为S=πr,那么圆面积变化速率为v=S′=2πr·r′;又因为r′=0.1 cm/s.从而r=10 cm时，v=2π×10×0.1 cm/s=2π cm/s.

7.C　设t s时刻圆面积为S，则S=πr,时刻t圆面积增加速率为S′,对应半径增加速率

u=r′,S′=2πr·r′,此时S′=10π cm/s,r=20 cm.

由10π=2π×20×r′,从而r′= cm/s.

8.C　由导数的几何意义可知，曲线在P点处切线斜率k=y′,

第9题图解

∴20=y′=n·()　　　　 ①

然后采用试值法，可知当n=5时满足方程①.

9.D　设光源S运动路程为l,则SB＝l=5t,此时影子Q运动路

程为x=AQ,又由于△APQ∽△BPS(如图).

从而,.

∴,∴x=25t,从而影子Q运动速率为v=x′=25.

10.B　点M的运动方程为x=rcost,那么点M的运动速率v=x′=-rsint.

二、填空题

11.　分析　从y′=1入手，写出两切线的方程.

解　y=-x+x+2x,∴y′=-3x+2x+2.所求直线与直线y=x平行.∴k=1.

命y′=1,即3x-2x-1=0,(3x+1)(x-1)=0,x=-或1,x=-时,

y=-(-)+-=-,x=1时,y=-1+1+2×1=2.

故切点为A,B(1,2)切线方程为:l:y+=x+,即x-y-=0,l:y-1=x-2,

即x-y+1=0,两切线间的距离为:d==.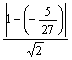

12.S′=-2esin(ωt+φ)+ωecos(ωt+φ).

S′=(e)′sin(ωt+φ)+e(sin(ωt+φ))′=-2esin(ωt+φ)+eωcos(ωt+φ).

13.　由y′=得P(x,y)的切线斜率k=,

P点的法线斜率k=-,

∴法线方程为y-y=-2(x-x),令y=0得x=,

即Q的横坐标为,RQ=x-x===.

点评　有关曲线切线的问题，一般都可用导数的几何意义完成，曲线在某一定点处的切线是惟一的，因此斜率也是惟一的（若存在的话），采用斜率相等这一重要关系，往往都可解决这类问题.

14.(0,-a),　∵y′=2x,y′=2a,

∴l:y-a=2a(x-a),令x=0得y=-a,

∴Q(0,-a),由k=2a=tan(90°-30°)=,∴a=.

三、解答题

15.分析　根据题目条件可列出多个不等式，但要用它们解出全部4个未知系数是困难的，问题在于，要回答本题的两个问题，是否必须求出所有的未知系数，想到这里，便会豁然开朗.

解　f ′(x)=3x-2ax,f ′(1)=3-2a

∵切线斜率为1,∴3-2a=1,a=1

3x-2ax=3x-2x

令3x-2x=1,x=1或-

故已知曲线斜率为1的切线有两条.

因为A在曲线上，∴c=1-1+b=b,

过点A的切线为y-c=x-1,即y=x+c-1,∴d=c-1.

当x=-时，y=(-)-(-)+c,

故相应切点为(-,c-).

切线方程为y-(c-)=x+,即y=x+c+.

两直线间距离为.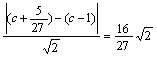

16.解　(1)函数y=x+2x的导数y′=2x+2,曲线C在点P(x,x+2x)处的切线方程是

y-(x+2x)=(2x+2)(x-x)

即y=(2x+2)x-x　　　　　 ①

函数y=-x+a的导数y′=-2x.

曲线C₂在点Q(x,-x+a)处的切线方程是y-(-x+a)=-2x(x-x)

即y=-2xx+x+a　　　　　　 ②

如果直线l是过P和Q的公切线，则①式和②式都是直线l的方程，

所以：

消去x，得2x+2x+1+a=0

若Δ=4-8(1+a)=0,即a=-，得x=-，x=-,

∴P(-,-)、Q(-,-)，P与Q重合，所以：当a=-时，C与C只有一条公切线，

公切线方程是：y=x-.

(2)由(1)知：当

Δ=4-8(1+a)>0即a<-时，P与Q不重合，此时C与C有两条公切线.

设一条公切线上的切点为P(x,y)、Q(x,y)，其中P∈C，Q∈C，则x+x=-1

y+y=(x+2x)+(-x+a)=x+2x-(x+1)+a=a-1

线段PQ的中点E.

同理，另一条公切线段P′Q′的中点也是.

∴当C与C有两条公切线时，相应的两公切线段相互平分.

点评　本题把导数与二次曲线位置关系融为一体，重在考查用导数的几何意义分析问题解决问题的能力.

17.解　(1)函数f(x)的定义域为(-1,+∞),f ′(x)=-1=-.

由f ′(x)<0及x>-1得x>0.∴当x∈(0,+∞)时，f(x)是减函数，即f(x)的单调递减区间为(0,+∞).

(2)由(1)知，当x∈(-1,0)时，f ′(x)>0;当x∈(0,+∞)时，f ′(x)<0.

因此，当x>-1时，f(x)≤f(0)，即ln(x+1)-x≤0.

∴ln(x+1)≤x.令g(x)=ln(x+1)+-1,

则g′(x)=-.

当x∈(-1,0)时，g′(x)<0；当x∈(0,+∞)时，g′(x)>0.

∴当x>-1时，g(x)≥g(0),即ln(x+1)+-1≥0,

∴ln(x+1)≥1-.

综上可知，当x>-1时，有1-≤ln(x+1)≤x.

18.解　(1)由图可知s=OC+CB.由三角函数定义可知：OC=rcosωt,CA=rsinωt,

所以，CB=,从而，

s=rcosωt+,此为滑块运动方程.

(2)s关于时间t的导数s′就是滑块运动速率v即

v=st′=(rcosωt+)′=-rωsinωt+,

v=-rωsinωt-

19.解　（1）s₁′=v,s₂′=at+v

s为匀速直线运动，速度为v;s为匀加速直线运动，加速度为a.

（2）s′=2πcos2πt.令s′=0,

即cos2πt=0,得2πt=kπ+,t=+.