高考数学复习—概率与统计练习试题卷-高考数学试题、数学高考试卷、模拟题、复习资料-高中数学试卷-试卷下载

高考数学复习—概率与统计练习试题卷

一、选择题(10×5′=50′)

1.设导弹发射的事故率为0.01,若发射导弹10次，其中出事故的次数为ξ,则下列结论正确的是(　　)

A.Eξ=0.1　　　　　　　　　　　　 B.P(ξ=k)=0.01^k·0.99^10-k

C.Dξ=0.1　　　　　　　　　　　　 D.P（ξ=k）=C0.99^k·0.01^10-k

2.一个盒子里装有相同大小的黑球10个，红球12个，白球4个，从中任取2个，其中白球的个数记为ξ,则下列算式中等于的是　 (　　)

A.P(0<ξ≤2)　　　　　　 B.P(ξ≤1)

C.Eξ　　　　　　　　　　 D.Dξ

3.已知随机变量ξ和η，其中η=12ξ+7,且Eη=34,若ξ的分布列如下表，则m的值为

ξ	1	2	3	4
P		m	n

A.　　　　　 B.　　　　　 C.　　　　　 D.

4.一整数等可能地在1、2、…、10中取值，以ξ记除得尽这一整数的正整数的个数，那么Eξ等于　　(　　)

A.2.6　　　　　 B.2.5　　　　　 C.2.7　　　　　 D.2.8

5.若ξ的分布列为：

ξ	0	1
P	p	q

其中p∈(0,1),则　　(　　)

A.Eξ=p,Dξ=p³　　　　 B.Eξ=p,Dξ=p²

C.Eξ=q,Dξ=q²D.Eξ=1-p,Dξ=p-p²

6.如果ξ是离散型随机变量，η=3ξ+2,那么　　(　　)

A.Eη=3Eξ+2,Dη=9Dξ　　　　　　　　　 B.Eη=3Eξ,Dη=3Dξ+2

C.Eη=3Eξ+2,Dη=9Eξ+4　　　　　　　　 D.Eη=3Eξ+4,Dη=3Dξ+2

7.设随机变量ξ～B（n,P）,且Eξ＝1.6，Dξ=1.28,则　 (　　)

A.n=8,P=0.2　　　　　　　 B.n=4,P=0.4

C.n=5,P=0.32　　　　　　 D.n=7,P=0.45

8.设掷1颗骰子的点数为ξ,则　　(　　)

A.Eξ=3.5,Dξ=3.5²　　　　　　　 B.Eξ=3.5,Dξ=

C.Eξ=3.5,Dξ=3.5　　　　　　　 D.Eξ=3.5,Dξ=

9.设离散型随机变量ξ满足Eξ＝-1，Dξ＝3，则E［3(ξ²-2)］等于　　(　　)

A.9　　　　　 B.6　　　　 C.30　　　　　 D.36

10.设随机变量ξ的分布列如下所示：

ξ	0	1	2
P

则函数F(x)=P(ξ≤x)(x∈R)的解析式为　　(　　)

A.F(x)=P(ξ≤x)=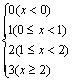　　　　　 B.F(x)=P(ξ≤x)=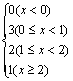

C.F(x)=P(ξ≤x)= 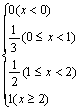　　　　　D.F(x)=P(ξ≤x)=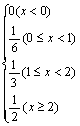

二、填空题（4×4′=16′）

11.已知某离散型随机变量ξ的数学期望Eξ=，ξ的分布列如下：

ξ	0	1	2	3
P	a			B

则a=　　　　　　　.

12.两名战士在一次射击比赛中，战士甲得1分、2分、3分的概率分别为0.4、0.1、0.5;战士乙得1分、2分、3分的概率分别为0.1、0.6、0.3,那么两名战士得胜希望大的是　　　　　　 .

13.某人有6把钥匙，其中只有一把能打开门，今任取一把试开，不能打开的除去，则打开此门所需试开次数ξ的数学期望Eξ=　　　　　 .

14.罐中有6个红球，4个白球，从中任取1球，记住颜色后再放回，连续摸取4次，设ξ为取得红球的次数，则ξ的期望Eξ=　　　　 .

三、解答题（4×10′+14′=54′）

15.某篮球队与其他6支篮球队依次进行6场比赛，每场均决出胜负，设这支篮球队与其他篮球队比赛胜场的事件是独立的，并且胜场的概率是.

(1)求这支篮球队首次胜场前已经负了两场的概率；

(2)求这支篮球队在6场比赛中恰好胜了3场的概率；

(3)求这支篮球队在6场比赛中胜场数的期望和方差.

16.某市出租车的起步价为6元，行驶路程不超过3km时，租车费为6元，若行驶路程超过3km，则按每超出1km(不足1km也按1km计程)收费3元计费.

设出租车一天行驶的路程数ξ（按整km数计算，不足1km的自动计为1km）是一个随机变量，则其收费也是一个随机变量.已知一个司机在某个月每次出车都超过了3 km,且一天的总路程数可能的取值是200、220、240、260、280、300（km），它们出现的概率依次是0.12、0.18、0.20、0.20、100a²+3a、4a.

(1)求这一个月中一天行驶路程ξ的分布列，并求ξ的数学期望和方差.

(2)求这一个月中一天所收租车费η的数学期望和方差.

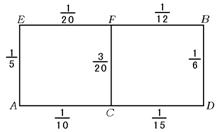
17.某先生居住在城镇的A处，准备开车到单位B处上班.若该地各路段发生堵车事件都是相互独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图所示(例如A→C→D算作两个路段：路段AC发生堵车事件的概率为,路段CD发生堵车事件的概率为).

(1)请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小;

(2)若记路线A→C→F→B中遇到堵车次数为随机变量ξ,求ξ的数学期望Eξ.

第17题图

18.一出租车司机从饭店到火车站途中有6个交通岗，假设他在各交通岗遇到红灯这一事件是相互独立的，并且概率都是.

(1)求这位司机遇到红灯前，已经通过了2个交通岗的概率；

(2)求这位司机在途中遇到红灯数ξ的期望和方差.

19.A有一个放有x个红球、y个白球、z个黄球的箱子（x、y、z≥1,x+y+z=6）,B有一个放有3个红球、2个白球、1个黄球的箱子，两人各自从自己的箱子中任取一球，规定当两球同色时为A胜，异色时为B胜.

(1)用x、y、z表示A胜的概率；

(2)若又规定当A取红、白、黄而得胜的得分分别为1、2、3；负则得0分，求使A得分的期望最大的x、y、z.

概率与统计练习100分参考答案

一、选择题

1.A　∵P(ξ=k)=C·0.01^k(1-0.01)^10-k,Eξ=nP=0.1.

2.B　作出概率分布可得.

3.A　本题考查随机变量的期望及有关的运算，由

η=12ξ+7Eη=12Eξ+734=12Eξ+7Eξ=

=1×+2×m+3×n+4×,

又+m+n+=1,联立求解可得m=,故选A.

4.C　P(ξ=1)=,P(ξ=2)=,P(ξ=3)=,P(ξ=4)=.

∴Eξ=+2×+3×+4×=2.7.

5.D　由于p＋q=1,所以q=1-p,从而Eξ=0×p+1×q=q=1-p,

Dξ=［0-(1-p)］²p+［1-(1-p)］²q=(1-p)²p+p²(1-p)=p-p²

6.A　设随机变量ξ的分布列是：

ξ	x₁	x₂	…	x_n_-1	x_n
P	P₁	P₂	…	P_n-₁	P_n

则η=3ξ+2的分布列为：

η	3x₁+2	3x₂+2	…	3x_n_-1+2	3x_n+2
P	P₁	P₂	…	P_n-₁	P_n

从而Eη=E(3ξ+2)=(3x₁+2)P₁+(3x₂+2)P₂+…+(3x_n_-1+2)P_n_-1+(3x_n+2)P_n

=3(x₁P₁+x₂P₂+…+x_n_-1P_n_-1+x_nP_n)+2(P₁+P₂+…+P_n-1+P_n)=3Eξ+2;

Dη=［(3x₁+2)-(3Eξ+2)］²P₁+［(3x²+2)-(3Eξ+2)］²P₂+…+［(3x_n_-1+2)-(3Eξ+2)］²P_n_-1+［(3x_n+2)-(3Eξ+2)］²P_n=9(x₁-Eξ)²P₁+9(x₂-Eξ)²P₂+…+9(x_n_-1-Eξ)²P_n_-1+9(x_n-Eξ)²P_n

=9［(x₁-Eξ)²P₁+(x₂-Eξ)²P₂+…+(x_n_-1-Eξ)²P_n_-1+(x_n-Eξ)²P_n］=9Dξ.

点评　对于随机变量ξ和η，如果η=aξ+b(a、b为常数)，则有Eη=aEξ+b,Dη=a²Dξ.

7.A　∵ξ~B(n,P),∴Eξ=nP,Dξ=nP(1-P),

从而有解之，得n=8,P=0.2.

8.B　随机变量ξ的分布列是：

ξ	1	2	3	4	5	6
P

从而Eξ=1×+2×+3×+4×+5×+6×=3.5,

Dξ=(1-3.5)²×+(2-3.5)²×+(3-3.5)²×+(4-3.5)²×+(5-3.5)²×+(6-3.5)²×=.

9.B　E［3(ξ²-2)］=E(3ξ²-6)=3Eξ²-6=3［Dξ+(Eξ)²］-6=6.

10.C　从表中可见，当x<0时，P（ξ≤x）=0;

当0≤x<1时，P(ξ≤x)=P(ξ=0)=;

当1≤x<2时，P（ξ≤x）=P(ξ=0)+P(ξ=1)=;

当x≥2时，P（ξ≤x）=P(ξ=0)+P(ξ=1)+P(ξ=2)=1.

点评　对于密度函数，要理解其意义，搞清它与概率分布的联系与区别.

二、填空题

11.　本题需运用离散型随机变量的期望等知识.

Eξ==0×a+1×+2×+3bb=.

又P(ξ=0)+P(ξ=1)+P(ξ=2)+P(ξ=3)=1

a+++=1a=.

12.乙　甲获胜的期望与方差分别是:

(Eξ)_甲=0.4×1+0.1×2+0.5×3=2.1,(Dξ)_甲=(2.1-1)²×0.4+(2.1-2)²×0.1+(2.1-3)²×0.5=0.89.

乙获胜的期望与方差分别是:

(Eξ)_乙=0.1×1+0.6×2+0.3×3=2.2,(Dξ)_乙=(2.2-1)²×0.1+(2.2-2)²×0.6+(2.2-3)²×0.3=0.456.

∵乙的期望高于甲，且乙的水平比甲稳定，故得胜希望大的是乙.

13.　Eξ=1×+2×+3×+4×+5×+6×=.

14.　因为是有放回地摸球，所以每次摸球（试验）摸得红球（成功）的概率均为,连续摸4次（做4次试验），ξ为取得红球（成功）的次数，则ξ~B,从而有Eξ=nP=4×=.

三、解答题

15.解　(1)p=(1-)²·=.

(2)6场胜3场的情况有C种.

∴p=C=20××=.

(3)由于ξ服从二项分布，即ξ～B(6,),

∴Eξ=6×=2,Dξ=6××(1-)=.

答：(1)这支篮球队首次胜场前已负两场的概率为;

(2)这支篮球队在6场比赛中恰胜3场的概率为;

(3)在6场比赛中这支篮球队胜场的期望为2,方差为.

点评　在二项分布ξ～B(n,p)中,期望Eξ=np,方差=npq.这两个公式只要求考生了解、会用，不要求给予证明.

16.解　（1）由概率分布的性质有0.12+0.18+0.20+0.20+100a²+3a+4a=1.

∴100a²+7a=0.3,∴1 000a²+70a-3=0,a=,或a=-(舍去)，即a=0.03,

∴100a²+3a=0.18,4a=0.12,∴ξ的分布列为

ξ	200	220	240	260	280	300
P	0.12	0.18	0.20	0.20	0.18	0.12

∴Eξ=200×0.12+220×0.18+240×0.20+260×0.20+280×0.18+300×0.12=250(km)

Dξ=50²×0.12+30²×0.18+10²×0.20+10²×0.20+30²×0.18+50²×0.12=964;

(2)由已知η=3ξ-3(ξ>3,ξ∈Z),∴Eη=E(3ξ-3)=3Eξ-3=3×250-3=747(元)

Dη=D(3ξ-3)=3²Dξ=8 676.

17.解　(1)记路段MN发生堵车事件为MN,因为各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，所以路线A→C→D→B中遇到堵车的概率P₁为

1-P(··)=1-P()·P()·()

=1-［1-P(AC)］［1-P(CD)］［1-P(DB)］=1-··=;

同理：路线A→C→F→B中遇到堵车的概率P₂为1-P(··)=(大于);路线A→E→F→B中遇到堵车的概率P₃为1-P(··)=(小于);

显然要使得由A到B路线途中发生堵车事件的概率最小，只可能在以上三条路线中选择.因此

选择路线A→C→F→B,可使得途中发生堵车事件的概率最小.

(2)路线A→C→F→B中遇到堵车次数ξ可取值为0,1,2,3.

P(ξ=0)=P(··)=.

P(ξ=1)=P(AC··)+P(·CF·)+P(··FB)

=××+××+××=.

P(ξ=2)=P(AC·CF·)+P(AC··FB)+P(·CF·FB)

=××+××+××=,

P(ξ=3)=P(AC·CF·FB)=××=,

Eξ=0×+1×+2×+3×=.

答：路线A→C→F→B中遇到堵车次数的数学期望为.

18.解　(1)因为这位司机第一二个交通岗未遇到红灯，在第三个交通岗遇到红灯，

所以P=(1-)(1-)×=.

(2)易知ξ~B(6,).∴Eξ=6×=2,Dξ=6××(1-)=.

19.解　(1)从两个箱子里各取1球，共CC=36种取法，

其中同色的取法有CC+CC+CC=3x+2y+z故A胜的概率为.

(2)设A得分为ξ,则ξ可能取值为0、1、2、3,其概率分别为

P(ξ=0)=1-=1-

P(ξ=1)=

P(ξ=2)=

P(ξ=3)=

∴Eξ=0×1-+1×+2×+3×=

∵x+y+z=6,∴Eξ=

∵x,y,z≥1,∴当x=1,y=4,z=1时，Eξ最大为.

高考数学复习—概率与统计练习试题卷

P

P

P

P

P

P n-1

P

P n-1

P

P

P_n-₁

P_n-₁