高考数学复习—直线与圆练习试题
第Ⅰ卷 (选择题 共40分)
一、选择题(10×4′=40′)
1.直线l与直线y=1、x-y-7=0分别交于P、Q两点,线段PQ的中点为(1,-1),则直线l的斜率为( )
A.![]() B.
B.![]() C.-
C.-![]() D.-
D.-![]()
2.点P在直线2x+y+10=0上,PA、PB与圆![]() 分别相切于A、B两点,则四边形PAOB面积的最小值为 ( )
分别相切于A、B两点,则四边形PAOB面积的最小值为 ( )
A.24 B.16 C.8 D.4
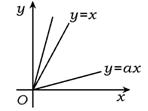
3.已知直线![]() :y=x,
:y=x,![]() :ax-y=0,其中a为实数,当这两直线的夹角θ∈(0,
:ax-y=0,其中a为实数,当这两直线的夹角θ∈(0,![]() )时,a的取值范围为 ( )
)时,a的取值范围为 ( )
A.(0,1) B.(![]() ,
,![]() ) C.(
) C.(![]() ,1)∪(1,
,1)∪(1,![]() ) D.(1,
) D.(1,![]() )
)
4.设a、b、k、p分别表示同一直线的横截距、纵截距、斜率和原点到直线的距离,则有( )
A.![]() B.k=
B.k=![]() C.
C.![]() =p D.a=-kb
=p D.a=-kb
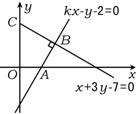
5.已知直线x+3y-7=0,kx-y-2=0和x轴、y轴围成四边形有外接圆,则实数k等于 ( )
A.-3 B.3 C.-6 D.6
6.若圆![]() (r>0)上恰有相异两点到直线4x-3y+25=0的距离等于1,则r的取值范围是( )
(r>0)上恰有相异两点到直线4x-3y+25=0的距离等于1,则r的取值范围是( )
A.[4,6]
B.![]() 4,6)
C.(4,6
4,6)
C.(4,6![]() D.(4,6)
D.(4,6)
7.直线![]() :
:![]() ,
,![]() :
:![]() ,则
,则![]() =-1是
=-1是![]() ⊥
⊥![]() 的 ( )
的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
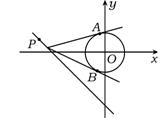
8.过圆![]() 外一点P(4,-1)引圆的两条切线,则经过两切点的直线方程为 ( )
外一点P(4,-1)引圆的两条切线,则经过两切点的直线方程为 ( )
A.4x-y-4=0 B.4x+y-4=0 C.4x+y+4=0 D.4x-y+4=0
9.倾斜角为60°,且过原点的直线被圆![]() (r>0)截得弦长恰好等于圆的半径,则a、b、r满足的条件是 ( )
(r>0)截得弦长恰好等于圆的半径,则a、b、r满足的条件是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.直线y=kx+1与圆![]() 的两个交点关于y轴对称,则k为 ( )
的两个交点关于y轴对称,则k为 ( )
A.-1 B.0 C.1 D.任何实数
第Ⅱ卷 (非选择题 共60分)
二、填空题(4×3′=12′)
11.若点P(a,b)与点Q(b+1,a-1)关于直线l对称,则直线l的方程是 .
12.已知圆![]() 的一条直径通过直线x-2y-3=0被圆截弦的中点,则该直径所在直线的方程为
.
的一条直径通过直线x-2y-3=0被圆截弦的中点,则该直径所在直线的方程为
.
13.关于x的方程kx+1=![]() 有且只有一个实根,则实数k的取值范围是
.
有且只有一个实根,则实数k的取值范围是
.
14.经过点P(-2,4),且以两圆![]() 和
和![]() 的公共弦为一条弦的圆的方程是
.
的公共弦为一条弦的圆的方程是
.
三、解答题(6×8′=48′)
15.若直线![]() :x+y+a=0,
:x+y+a=0,![]() :x+ay+1=0,
:x+ay+1=0,![]() :ax+y+1=0能围成三角形,求a的取值范围.
:ax+y+1=0能围成三角形,求a的取值范围.
16.已知点P是直线l上的一点,将直线l绕点P逆时针方向旋转α(0<α<![]() )所得直线
)所得直线![]() 的方程为3x-y-4=0,若继续绕点P逆时针方向旋转
的方程为3x-y-4=0,若继续绕点P逆时针方向旋转![]() ,则得
,则得![]() 的方程为x+2y+1=0,试求直线l的方程.
的方程为x+2y+1=0,试求直线l的方程.
17.设P是圆M:![]() 上的动点,它关于A(9,0)的对称点为Q,把P绕原点依逆时针方向旋转90°到点S,求SQ的最值.
上的动点,它关于A(9,0)的对称点为Q,把P绕原点依逆时针方向旋转90°到点S,求SQ的最值.
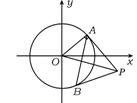
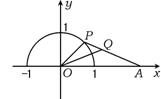
18.已知点A(3,0),点P在圆![]() 的上半圆周上,∠AOP的平分线交PA于Q,求点Q的轨迹方程.
的上半圆周上,∠AOP的平分线交PA于Q,求点Q的轨迹方程.
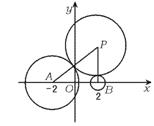
19.如图,已知⊙A:![]() ,⊙B:
,⊙B:![]() ,动圆P与⊙A、⊙B都外切.
,动圆P与⊙A、⊙B都外切.
(1)求动圆圆心P的轨迹方程,并说明轨迹是什么曲线;
(2)若直线y=kx+1与(1)中的曲线有两个不同的交点![]() 、
、![]() ,求k的取值范围;
,求k的取值范围;
(3)若直线l垂直平分(2)中的弦![]() ,求l在y轴上的截距b的取值范围.
,求l在y轴上的截距b的取值范围.
|
20.已知圆C:![]() ,是否存在斜率为1的直线l,使得l被圆C截得弦AB为直径的圆过原点?若存在,求出l的方程;若不存在,说明理由.
,是否存在斜率为1的直线l,使得l被圆C截得弦AB为直径的圆过原点?若存在,求出l的方程;若不存在,说明理由.
直线与圆练习参考答案
1.C 方法1 设直线l为y=kx+b,分别与y=1,x-y-7=0联立解得P
(-![]() ,1),Q (
,1),Q (![]() ,
,![]() ).由PQ中点为(1,-1),∴
).由PQ中点为(1,-1),∴![]() ,且1+
,且1+![]() =-2,∴k=-
=-2,∴k=-![]() ,故选C.
,故选C.
方法2 设P (a,1),Q (b+7,b),因PQ的中点为(1,-1),
∴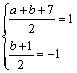 ,解得
,解得![]() ,故P为(-2,1),Q为(4,-3),
,故P为(-2,1),Q为(4,-3),
∴![]() ,故选C.
,故选C.
2.C 如图,![]() =
=![]() =2
=2![]() .
.
要求![]() 的最小值,只需求PO的最小值即可.
的最小值,只需求PO的最小值即可.
|
3.C 如图,设直线y=ax的倾斜角为α,
则α≠![]() ,∴α-
,∴α-![]() <
<![]() ,
,
∴![]() <α<
<α<![]() ,且α≠
,且α≠![]() .a=tanα∈(
.a=tanα∈(![]() ,1)∪(1,
,1)∪(1,![]() ).
).
4.A 应用点到直线的距离公式,选A.
| ||||
| ||||
5.B 如图,设围成四边形为OABC,因OABC有外接圆,且∠AOC=90°,故∠ABC=90°.
∴两条直线x+3y-7=0,kx-y-2=0互相垂直,(-![]() )·k=-1,即k=3,故选B.
)·k=-1,即k=3,故选B.
说明 运用圆的几何性质是解决圆的问题的有效途径.
6.D 如图,设l:4x-3y+25=0,与l平行且距离等于1的直线为4x-3y+b=0.
∴![]() 或b=30.
或b=30.
![]() :4x-3y+20=0,
:4x-3y+20=0,![]() :4x-3y+30=0.
:4x-3y+30=0.
|
故满足条件的r取值范围(4,6).
实际上,圆![]() 没有点到直线4x-3y+25=0的距离等于1,
没有点到直线4x-3y+25=0的距离等于1,
则0<r<4,若圆上只有一点到直线4x-3y+25=0的距离等于1,
则r=4,类似可求出圆上有三点、四点到直线的距离等于1
的r的取值范围.
7.A 由![]() ,可得
,可得![]() ⊥
⊥![]() ,∴选A.
,∴选A.
|
∵![]() ,∴
,∴![]() .故排除B、C.
.故排除B、C.
又由图可知,AB在y轴的截距为负,故排除D,所以选A.
方法2 设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
由AP⊥OA可得![]() ·
·![]() =-1,
=-1,
即![]() .∴
.∴![]() ,又
,又![]() ,
,
∴![]() .
.
同理可得![]() ,∴AB直线为-4x+y+4=0,即4x-y-4=0.
,∴AB直线为-4x+y+4=0,即4x-y-4=0.
方法3 设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),则切线PA为
),则切线PA为![]() ,
,![]() .
.
∴![]() ,
,![]() ,∴A、B在直线4x-y-4=0上.
,∴A、B在直线4x-y-4=0上.
另:此题可推广到一般结论,若P (![]() ,
,![]() )为圆
)为圆![]() (r>0)外一点,过P引圆的两条切线,则经过两切点的直线方程为
(r>0)外一点,过P引圆的两条切线,则经过两切点的直线方程为![]() .
.
9.A 直线方程为![]() ,则圆心(a,b)到直线
,则圆心(a,b)到直线![]() x-y=0的距离为d=
x-y=0的距离为d=![]() ,又因截得弦长恰好等于圆的半径,故d=
,又因截得弦长恰好等于圆的半径,故d=![]() r,∴
r,∴![]() a-b=
a-b=![]() r,故选A.
r,故选A.
10.B 方法1 将y=kx+1代入![]() 中有
中有![]() .
.
设交点为 A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),∵A、B关于y轴对称,∴
),∵A、B关于y轴对称,∴![]() ,
,
∴k=0.故选B.
方法2 因直线与圆的两个交点A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )关于y轴对称
)关于y轴对称
∴![]() ,
,![]() ,故圆心在y轴上,∴k=0,故选B.
,故圆心在y轴上,∴k=0,故选B.
11.x-y-1=0 P、Q关于直线l对称,故![]() =-1且PQ中点在l上,
=-1且PQ中点在l上,
∴![]() ,又PQ中点为(
,又PQ中点为(![]() ,
,![]() ),
),
∴l的方程为y-![]() =x-
=x-![]() ,即x-y-1=0.此题也可将a,b赋特殊值去求直线l.
,即x-y-1=0.此题也可将a,b赋特殊值去求直线l.
12.2x+y-3=0 由圆的几何意义知该直径与直线x-2y-3=0垂直.故该直径方程为y+1=-2(x-2),即2x+y-3=0.
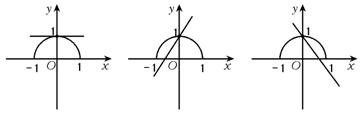
13.{kk>1或k=0或k<-1} 画出函数y=kx+1、y=![]() 的图象,两曲线相切及只有一个交点时如图所示.
的图象,两曲线相切及只有一个交点时如图所示.
|
14.![]() 设圆的方程为
设圆的方程为![]() 经过P(-2,4),
经过P(-2,4),
∴![]() ,
,
∴λ=-2,∴所求的圆的方程为![]() .
.
15.解 由![]() 、
、![]() 相交,需1·a-1·1≠0,得a≠1,此时解方程组
相交,需1·a-1·1≠0,得a≠1,此时解方程组![]() ,
,
可解得![]() 即
即![]() 、
、![]() 的交点为(-1-a,1),由
的交点为(-1-a,1),由![]() 、
、![]() 相交,
相交,
需1·1-1·a≠0,∴a≠1,由![]() ,
,![]() 相交,需1·1-a·a≠0,∴a≠±1,又(-1-a,1)
相交,需1·1-a·a≠0,∴a≠±1,又(-1-a,1)![]()
![]() ,
,
∴a·(-1-a)+1+1≠0,得a≠1且a≠-2,
综上所述,a∈R且a≠±1且a≠-2,能保证三交点(-1-a,1),(1,-1-a)、(-1-a,-1+a+![]() )互不重合,所以所求a的范围为a∈(-∞,-2)∪(-2,-1)∪(-1,1)∪(1,+∞).
)互不重合,所以所求a的范围为a∈(-∞,-2)∪(-2,-1)∪(-1,1)∪(1,+∞).
16.解 由已知条件知P为直线3x-y-4=0和直线x+2y+1=0的交点,联立两直线方程得
![]() ,∴
,∴![]() .∴P点为(1,-1).
.∴P点为(1,-1).
又l与![]() 垂直,故l的方程为y+1=2(x-1),即l的方程为2x-y-3=0.
垂直,故l的方程为y+1=2(x-1),即l的方程为2x-y-3=0.
17.解 设P(x,y),则Q(18-x,-y),记P点对应的复数为x+yi,
则S点对应的复数为:(x+yi)·i=-y+xi,即S(-y,x),
∴SQ=![]()
=![]()
其中![]() 可以看作是点P到定点B(9,-9)的距离,其最大值为MB+r=2
可以看作是点P到定点B(9,-9)的距离,其最大值为MB+r=2![]() +1,最小值为MB-r=2
+1,最小值为MB-r=2![]() -1,则SQ的最大值为2
-1,则SQ的最大值为2![]() +
+![]() ,SQ的最小值为2
,SQ的最小值为2![]() -
-![]() .
.
18.解 方法1 如图,设P(![]() ,
,![]() )(
)(![]() >0),Q(x,y).
>0),Q(x,y).
|
∴Q分PA的比为![]() .
.
∴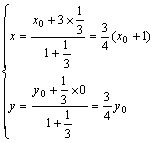 即
即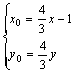 .
.
又因![]() ,且
,且![]() >0,∴
>0,∴![]() .
.
∴Q的轨迹方程为![]() (y>0).
(y>0).
方法2 设∠AOP=α,α∈(0,π),则P(cosα,sinα),∠AOQ=![]() ,
,
则OQ直线方程为y=x·tan![]() =kx ①
=kx ①
![]() ,∴直线PA方程为y=
,∴直线PA方程为y=![]() (x-3) ②
(x-3) ②
由Q满足①②且k=tan![]() .
.
由②得y=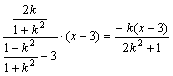 .
.
消去k有y=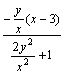 ,∴
,∴![]() ,由图知y>0.
,由图知y>0.
故所求Q点轨迹方程为![]() (y>0).
(y>0).
说明 上述两种方程为求轨迹的基本方法、相关点及参数法.
|
由题设,有PA=R+![]() ,PB=R+
,PB=R+![]() ,∴PA-PB=2.
,∴PA-PB=2.
∴⊙P的圆心轨迹是实轴长为2,焦点在x轴上,且焦距长
为4的双曲线的右支,其方程为![]() (x>0).
(x>0).
(2)由方程组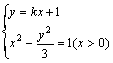 ,有
,有![]() (x>0).
①
(x>0).
①
因为直线与双曲线有两个不同交点,
∴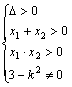 .从而,有
.从而,有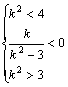
![]()
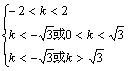 . ∴-2<k<-
. ∴-2<k<-![]() .
.
(3)设![]() 的中点为M(
的中点为M(![]() 、
、![]() ),则
),则![]() =
=![]() .
.
又M在y=kx+1上,∴![]() =k
=k![]() +1=
+1=![]() .
.
∴M(![]() ,
,![]() ).
).
∴![]() 的垂直平分线l的方程为:y-
的垂直平分线l的方程为:y-![]() =-
=-![]() (x-
(x-![]() ),即y-
),即y-![]() =-
=-![]() (x-
(x-![]() ).
).
令x=0,得截距b=![]() ,k∈(-2,-
,k∈(-2,-![]() ),又-2<k<-
),又-2<k<-![]() ,∴-1<3-
,∴-1<3-![]() <0.∴b<-4.
<0.∴b<-4.
20.解 假设存在这样的直线,设直线l方程为y=x+b.
方法1 将y=x+b代入圆的方程有![]() .
.
由题设知OA⊥OB,设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),
),
∴![]()
![]() +
+![]()
![]() =0.
=0.
又![]()
![]() =(
=(![]() +b)(
+b)(![]() +b)=
+b)=![]()
![]() +b(
+b(![]() +
+![]() )+
)+![]() ,∴2
,∴2![]()
![]() +b(
+b(![]() +
+![]() )+
)+![]() =0.
=0.
又∵![]() +
+![]() =-(b+1),
=-(b+1),![]()
![]() =2b-2+
=2b-2+![]() ,
,
∴2(![]() +2b-2)-b(b+1)+
+2b-2)-b(b+1)+ ![]() =0.
=0.
∴b=1或b=-4.此时Δ=![]() ,
,
∴存在这样的直线l:y=x+1或y=x-4满足题设.
方法2 设过圆C与l的交点的圆系D为![]()
即![]() .
.
圆心为(-![]() ,-
,-![]() ),在直线y=x+b上,
),在直线y=x+b上,
∴-![]() =-
=-![]() +b,即λ=3+b.
①
+b,即λ=3+b.
①
又圆D过原点,∴bλ-4=0. ②
由①②得,![]() ,即b=1或b=-4.
,即b=1或b=-4.
此时圆D的方程存在.故存在直线y=x+1或y=x-4.