高考数学复习—立体几何练习试卷
第Ⅰ卷 (选择题 共50分)
一、选择题(10×5′=50′)
|
过O的动平面与P-ABC的三条侧棱或其延长线的交点分别记
为Q、R、S，则
( )
A.有最大值而无最小值
B.有最小值而无最大值
C.既有最大值又有最小值，且最大值与最小值不等
D.是一个与平面QRS位置无关的常量
2.在正n棱锥中，相邻两侧面所成的二面角的取值范围是 ( )
A.
B.
C.
D.
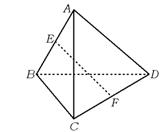
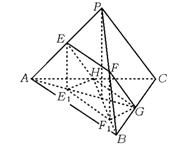
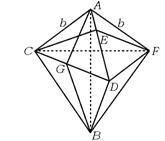
3.正三棱锥P-ABC的底面边长为2a,点E、F、G、H分别是PA、PB、BC、AC的中点，则四边形EFGH的面积的取值范围是 ( )
A.(0,+∞) B.
C.
D.
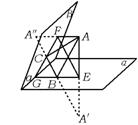
4.已知二面角α-a-β为60°，点A在此二面角内，且点A到平面α、β的距离分别是AE=4，AF=2，若B∈α,C∈β,则△ABC的周长的最小值是 ( )
A.4
B.2
C.4
D.2
|
使得
=λ(0<λ<+∞),记f (λ)=αλ+βλ,其中αλ表示EF
与AC所成的角，βλ表示EF与BD所成的角，则 ( )
A.f (λ)在(0,+∞)单调增加
B.f (λ)在(0,+∞)单调减少
C.f (λ)在(0,1)单调增加,在(1,+∞)单调减少
D.f (λ)在(0,+∞)为常数
6.直线a∥平面β,直线a到平面β的距离为1，则到直线a的距离与平面β的距离都等于
的点的集合是
( )
A.一条直线 B.一个平面 C.两条平行直线 D.两个平面
7.正四棱锥底面积为Q，侧面积为S，则它的体积为 ( )
A.
B.
C.
D.
8.已知球O的半径为R，A、B是球面上任意两点，则弦长AB的取值范围为 ( )
A.［0,2R］
B.(0,2R
C.（0,2R） D.［R,2R］
9.已知平面α∩平面β=l,m是平面α内的一条直线，则在平面β内 （ ）
A..一定存在直线与直线m平行，也一定存在直线与直线m垂直
B.一定存在直线与直线m平行，但不一定存在直线与直线m垂直
|
线m垂直
D.不一定存在直线与直线m平行，也不一定存在直线与
直线m垂直
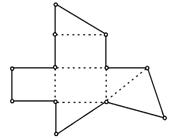
10.如图为一个简单多面体的表面展开图（沿图中虚线折
叠即可还原），则这个多面体的顶点数为 ( )
A.6 B.7 C.8 D.9
二、填空题（4×4′=16′）
11.边长为a的等边三角形内任一点到三边距离之和为定值，这个定值为 ;推广到空间，棱长为a的正四面体内任一点到各面距离之和为 .
12.在△ABC中，AB=9，AC=15，∠BAC=120°，其所在平面外一点P到A、B、C三个顶点的距离都是14，则P点到直线BC的距离为 .
13.已知将给定的两个全等的正三棱锥的底面粘在一起，恰得到一个所有二面角都相等的六面体，并且该六面体的最短棱的长为2，则最远的两顶点间的距离是 .
14.有120个等球密布在正四面体A-BCD内，问此正四面体的底部放有 个球.
三、解答题（4×10′+14′=54′）
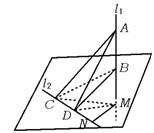
15.定直线l1⊥平面α,垂足为M，动直线l2在平面α内过定点N，但不过定点M.MN=a为定值，在l1、l2上分别有动线段AB=b,CD=c.b、c为定值.问在什么情况下四面体ABCD的体积最大？最大值是多少？
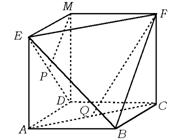
16.如图所示，已知四边形ABCD、EADM和MDCF都是边长为a的正方形，点P、Q分别是ED和AC的中点，求：
|
与
所成的角；
（2）P点到平面EFB的距离;
（3）异面直线PM与FQ的距离.
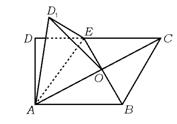
17.如图，在梯形ABCD中，AB∥CD，∠ADC＝90°,3AD=DC=3,AB=2,E是CD上一点，满足DE＝1，连结AE，将△DAE沿AE折起到△D1AE的位置，使得∠D1AB＝60°,设AC与BE的交点为O.
(1)试用基向量
,
,
表示向量
(2)求异面直线OD1与AE所成的角.
(3)判断平面D1AE与平面ABCE是否垂直，并说明理由.
|
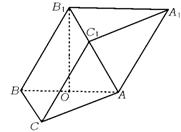
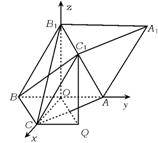
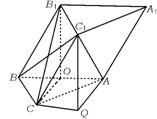
18.如图，在斜棱柱ABC—A1B1C1中，底面为正三角形，侧棱长等于底面边长，且侧棱与底面所成的角为60°,顶点B1在底面ABC上的射影O恰好是AB的中点.
（1）求证：B1C⊥C1A；
（2）求二面角C1-AB-C的大小.
|
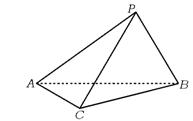
19.如图所示，在三棱锥P-ABC中，PA=PB=PC，BC=2a,AC=a,AB=a,点P到平面ABC的距离为
a.
（1）求二面角P-AC-B的大小；
（2）求点B到平面PAC的距离.
|
立体几何练习参考答案
一、选择题
1.D 设正三棱锥P-ABC中，各棱之间的夹角为α,棱与底面夹角为β,h为点S到平面PQR的距离，则VS-PQR=
S△PQR·h=(
PQ·PR·sinα)·PS·sinβ,另一方面，记O到各平面的距离为d,则有VS-PQR=VO-PQR+VO-PRS+VO-PQS=S△PQR·d+S△PRS·d+S△PQS·d=
··PQ·PR·sinα+·PS·PR·sinα+··PQ·PS·sinα.故有PQ·PR·PS·sinβ=d(PQ·PR+PR·PS+PQ·PS)，即=
=常量.
2.B 设正n棱锥的高为h,相邻两侧面所成二面角为θ.当h→0时，正n棱锥的极限为正n边形，这时相邻两侧面所成二面角为平面角，即二面角θ→π.
当h→∞时，正n棱锥的极限为正n棱柱，这时相邻两侧面所成二面角为正n边形的内角，即θ→
π.故选B.
3.B 如图，易知四边形EFGH为矩形，当P→底面△ABC的中心O时，矩形EFGH→矩形E1F1GH.
=E1F1·F1G=a·
a=a2.
即S矩形EFGH→a2.当P→∞时，S矩形EFGH→∞.
∴S矩形EFGH∈.故选B.
|
|
4.C 如图，∵a⊥AE,a⊥AF,∴a⊥平面AEF.
设a交平面AEF于点G，则∠EGF是二面角α-a-β的平面角，∠EGF=60°,∠EAF=120°,且易知当△ABC的周长最小时，B∈EG,C∈FG.
设点A关于平面α的对称点为A′,点A关于平面β的对称点为A″,连结A′A″,分别交线段EG
、FG于点B、C,则此时△ABC的周长最短，记为l.由中位线定理及余弦定理得
l=2EF=2
=4.
5.D 因为ABCD是正四面体，故AC⊥BD,作EG∥AC交BC于G，连结GF，则αλ=∠GEF,且
,
∴GF∥BD,故GF⊥EG,且βλ=∠EFG,∴f (λ)=αλ+βλ=90°为常数.
6.C 这两条直线在距a为
的平面上，分布在a在该平面上的射影的两侧.
7.A 设正四棱锥各棱长均为1，则Q=1，S=，此时，正四棱锥的高h=
,
∴V=Qh=
,将Q=1，S=代入选择支，知A正确.
8.B 考虑A、B两点在球面上无限靠近但又不重合，及A、B两点应为直径的两端点时的情况.
点评 若忽视几何里的两点、两直线、两平面等均应是相异的两元素，就会误选A，球的最长弦就是直径，但球没有最短弦.
9.C 若m∥l，则β内必有与m平行的直线；若m与l相交，则β内无直线与m平行.
∴不一定存在直线与直线m平行，排除A、B.又β内一定存在与m在β内的射影垂直的直线，由三垂线定理知，β内一定存在直线与m垂直,故选C.
10.B 本题考查简单多面体的表面展开与翻折，着重考查考生的空间想像能力,该多面体是正方体切割掉一个顶点，故有7个顶点.
二、填空题
11.
;
a 本题通过等积找规律.
12.
分析 P点到A、B、C距离相等，故P点在平面ABC上的射影是三角形ABC的外心，故可由△ABC的已知条件求出△ABC外接圆半径，进而求得P点到平面ABC的距离，及外心到直线BC的距离，从而最终解决问题.
解 记P点在平面ABC上的射影为O，则AO、BO、CO分别是PA、PB、PC在平面ABC上的射影
∵PA=PB=PC,∴OA=OB=OC,
∴O为△ABC的外心.
在△ABC中，BC=
=21
由正弦定理，2R=
,∴R=7
P点到平面ABC的距离为
.
O点到直线BC的距离OD=
(D为BC边的中点)
∵OP⊥平面ABC，OD⊥BC,∴PD⊥BC.
∴P到BC的距离PD=
.
13.3 如图所示，作CE⊥AD，连结EF，易证EF⊥AD,
|
CD的中点，同理∠AGB为面ACD和面BCD所成二面角的
平面角，由已知∠CEF=∠AGB.
设底面△CDF的边长为2a,侧棱AD长为b.在△ACD中，
CE·b=AG·2a,所以CE=
在△ABC中，易求得AB=2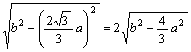
,
由△CEF∽△AGB得
,即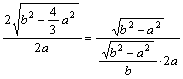
解得b=
a,因此b=2时，2a=3,∴最远的两顶点间距离为3.
14.36 正四面体ABCD的底部是正△BCD,假设离BC边最近的球有n个，则与底面△BCD相切的球也有n排，各排球的个数分别为n、n-1、…、3、2、1,这样与底面相切的球共有1+2+…+n=
个.由于正四面体各面都是正三角形.因此，正四面体内必有n层球，自上而下称为：第1层、第2
层、…第n层，那么第n-1层，第n-2层，…第2层，第1层球的个数分别是：
1+2+…+n=、1+2+…+n-1=
,
1+2=
,1=
∴
即
n(n+1)(n+2)=120.
即(n-8)(n2+11n+90)=0,∴n=8,因此正四面体内共有8层小球，其底部所放球数为
=36(个).
三、解答题
|
解 如图，连结MC、MD，则
∵AM⊥平面MDC，BM⊥平面MDC
∴VA-BCD=VA-MDC-VB-MDC=S△MDC·(AM-BM)
=S△MDC·AB
设M到CD的距离为x,则S△MDC=CD·x=cx,
∴VA-BCD=×cx·b=bcx
∵x≤MN=a,∴当x=a时，
即MN为l1与l2的公垂线时，VA-BCD最大，它的最大值为abc.
点评 x≤MN,包含x=MN,也包含x<MN,垂线段小于斜线段.
16.解 建立空间直角坐标系，使得D(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0)，M（0,0,a）,E(a,0,a)，F（0,a,a），
则由中点坐标公式得P(
,0,),Q(,,0),
(1)
所以=(-,0,),(,-,-a),·=(-)×+0+×(-a)=-
a2,
且=a,=
a,所以cos
,
=
.
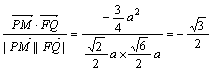故得两向量所成的角为150°;
(2)
设n=(x,y,z)是平面EFB的单位法向量，即n=1,n⊥平面EFB，所以n⊥
,且n⊥
,
又=(-a,a,0)，=（0,-a,a）,即有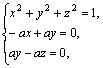
得其中的一个解是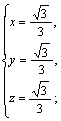
∴n=
,
=
,
设所求距离为d,则d=·n=
;
(3) 设e=(x1,y1,z1)是两异面直线的公垂线上的单位方向向量，
则由=
,=
,
得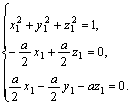
求得其中的一个e=
，
而
=(0,a,0)，设所求距离为m,则m=]·e=-a=a.
17.解 （1）根据已知，可得四边形ABCE为平行四边形，所以O为BE中点.
.
(2)
∵(
)2=(
-
-
)2=
,
∴=
.
∴cos<,>=
,
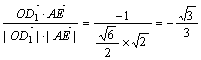所以OD1与AE所成角为arccos
.
(3)设AE的中点为M，则
=-.
∵·=·-·=1×2×cos60°-×
×2cos45°=0,
∴⊥.
·=·-
=cos 45°-×()2=0,∴⊥.
所以MD1垂直于平面ABCE内两条相交直线,∴MD1⊥平面ABCE.
而D1M平面AD1E，所以平面AD1E⊥平面ABCE.
18.(1)解法一 连结BC1、CO，∵B1O⊥平面ABC，CO⊥AB，∴B1C⊥AB，
又∵在菱形BB1C1C中，B1C⊥BC1，
∴B1C⊥平面ABC1，∴B1C⊥C1A.
（2）作C1Q⊥平面ABC于Q点，连接AQ，
∴∠C1CQ是侧棱与底面所成的角，即∠C1CQ=60°,
在△C1CQ中，CQ=CC1=AO，C1Q=
CC1，
由BC，B1C1，OQ平行且相等，又∵CO⊥AB,∴QA⊥AB,∴C1A⊥AB,
∴∠QAC1是二面角C1-AB-C的平面角,
在△AQC1中，C1Q=AQ，∴∠QAC1=45°
| ||||
| ||||
解法二 （1）以O为原点，OC所在直线为x轴，AB所在直线为y轴，建立空间直角坐标系，如图，
∵B1O⊥平面ABC，
∴∠B1BO是侧棱与底面所成角，∴∠B1BO=60°.
设棱长为2a,则OB1=a,BO=a,又CO为正三角形的中线，∴CO=a.
则A(0,a,0),B(0,-a,0),C(a,0,0),B1(0,0,a),C1(a,a,a).
=(a,0,-a),
=(-a,0,-a).
∵·=-3a2+0+3a2=0,∴B1C⊥C1A.
(2)在△C1AB中，=
a,
=（a,2a,a）=
a,=2a,
∴S△C1AB=a2,
作C1Q⊥平面ABC于Q点，则Q(a,a,0).
∴S△ABQ=a2,设二面角C1-AB-C的平面角为θ,
则cosθ=
.
二面角C1-AB-C的平面角为45°.
19.（1）解法一 由条件知△ABC为直角三角形，∠BAC=90°,
∵PA=PB=PC,∴点P在平面ABC上的射影是△ABC的外心，即斜边BC的中点E，取AC中点D，连结PD、DE、PE，PE⊥平面ABC.
|
DE⊥AC(∵DE∥AB).∴AC⊥PD,∠PDE为二面角P-AC-B的平面角.
tanPDE=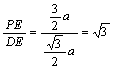
,
∴∠PDE=60°,故二面角P-AC-B的平面角为60°.
解法二 设O为BC的中点，则可证明PO⊥面ABC，建立如图空间直角坐标系，
则A
,B(-a,0,0),C(a,0,0),P
,
AC中点D
,
=
,
=
∵AB⊥AC,PA=PC,PD⊥AC,
cos<,>即为二面角P-AC-B的余弦值.
而cos<,>=
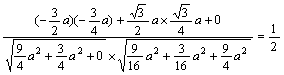
二面角P-AC-B的平面角为60°
(2)解法一 PD=
,
S△APC=·AC·PD=
设点B到平面PAC的距离为h,
则由VP-ABC=VB-APC得
·S△ABC·PE=·S△APC·h,
h=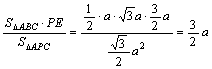
.
故点B到平面PAC的距离为
.
解法二 点E到平面PAC的距离容易求得，为
a,而点B到平面PAC的距离是其2倍,
∴点B到平面PAC的距离为.