高三数学上学期第一次摸底考试试题

高三数学上学期第一次摸底考试试题

本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 共150分，考试时间120分钟.

注意事项：

1．第Ⅰ卷的答案用2B铅笔涂在答题卡上，第Ⅱ卷的答案或解答过程均写在答题纸内的

　 指定处，写在试题卷上的无效．

2．答题前，考生务必将自己的“班级”、“学号”、“姓名”写在答题卡和答题纸上．

3．考试结束后，只交答题卡和答题纸．

第Ⅰ卷（选择题）

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知全集,集合，则集合　　　 （　　）

　　　 A． {1, 2, 3, 4}　 　B．{2, 3, 4}　 　　　　C．{1,5}  　　　　　　　D．{5}

2．设函数，则　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 　　　　　　　　　B． 0　　　 　　　　　C．1　　　　　　　　　D．4

3． 曲线在点P(1,2)处的切线方程是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A． 　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　 D．

4．已知、是两个不同平面，、是两不同直线，下列命题中的假命题是　　（　　）

　　　 A．　　　　　　　　 B．

　　　 C．　　　　　　　 D．

5．曲线在点处的切线与坐标轴围成的三角形面积为　　　　　　　　 （　　）

　　　 A．　　 　　　　　　 B．　　　　　　　　　  C．　　  　　　　　D．

6． 函数在[0, 2]上最小值是　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　B．　　　　　　　　C．　　　　  D．

7．已知一个球的直径为，则此球的表面积为　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．　 　　　　　　　 B． 　　　　　　　　 C．　　　 　　D．

8．若的展开式的二项式系数之和为64，则展开式的常数项为　　　　　　　　　 （　　）

　　　 A． 10　　　　　　　　B． 20　　　　　　　　　C．30　　　　　　　　D．120

9．由数字1，2，3，4，5所组成的三位数中，其各个数字之和为9的三位数共有　（　　）

　　　 A．16个　　　　　　　　　B．18个　　　　　　　C．19个　 　　　　　　 D．21个

1,3,5

10．P为抛物线上的任意一点，则P到直线的最短距离为　　　 （　　）

　　　 A．　　　　　　　　　B． 　　　　　　　C．　　　　　　　　D．0

11．设函数是R上以5为周期的可导偶函数，则曲线在处的切线的斜率为　　　　　　　　　　　 （　　）

　　　 A． 　　　　　　　B． 0　 　　　　　　　　 C．　 　　　　　　　　 D．5

12．设，且，则下列结论必成立的是

　　　 A．＞　　　　　 B．+＞0 　　　　C．＜ 　　　　　　D．＞

1,3,5

第Ⅱ卷（非选择题　共90分）

二、填空题：本大题共4小题，每小题5分，共20分．

13．的单调减区间是　　　　　　 

14．从4名男生和6名女生，选出3名奥运火炬手，要求至少包含1名男生，则不同的选法共有　　　　　　

15．某校现有高一学生210人，高二学生270人，高三学生300人，校学生会采用分层抽样的方法从这三个的学生中随机抽取n名学生进行问卷调查，如果已知从高一学生中抽取的人数为7，那么从高三学生中抽取的人数为　　　　　 

16．在正方体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是　　　　　　　　　 （写出所有正确结论的编号）.

①矩形；

②不是矩形的平行四边形；

③有三个面为等腰直角三角形，有一个面为等边三角形的四面体；

④每个面都是等边三角形的四面体；

⑤每个面都是直角三角形的四面体.

三、解答题（本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤）

17．（本题满分10分）

已知集合，若,求实数的取值范围．

18．（本题满分12分）

规定，其中R，m是正整数．

　 （Ⅰ）求的值；

　 （Ⅱ）设，当为何值时，的值最小？求出最小值.

19．（本题满分12分）

袋中装有四个标号为2、3、4、5的均匀小球，从中有放回地摸球两次，记其标号依次为,.

　 （Ⅰ）求使为偶数的概率；

　 （Ⅱ）求使的概率.

　　

20．（本题满分12分）

已知函数经过点M(1,4)，在点M处的切线恰与直线垂直

　 （Ⅰ）求a,b的值

　 （Ⅱ）若函数在区间[]上单调递增，求实数m的取值范围．

　　　　　

21．（本题满分12分）

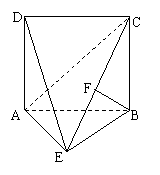如图，直二面角D—AB—E中，四边形ABCD是边长为2的正方形，AE=EB，F为CE上的点，且BF⊥平面ACE.

　 （Ⅰ）求证AE⊥平面BCE；

　 （Ⅱ）求二面角B—AC—E的正切值.　　　　　　　　　　　　　 

22．（本题满分12分）

设函数的图象关于原点对称，且 时，取极小值．

　 （Ⅰ）求a，b，c，d的值

　 （Ⅱ）当x∈[－1，1]时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论

　 （Ⅲ）若时，求证.

参考答案

一、选择题：

1,3,5

1．C　 2．B　 3．A　　4．B　　5．A　　6．A　　7．A　　8．B　　9．C　

10．B　　11．B　　12．D

二、填空题：

13．；　14．100；　　 15．10；　　16．①③④⑤

三、解答题

17．解： 由 ，解得．∴……………3分

又由，解得或．

∴……………………………………………………6分

∵，则有 ，即，

故所求实数的取值范围是．………………………………………10分

18．解：（Ⅰ）；………………………………4分

　 （Ⅱ），

当时，（当且仅当时取等号），

∴当时，有最小值，最小值为.………………………12分

19．解：（Ⅰ）欲使为偶数，则、同奇同偶，

∴.………………………………………………………6分

　 （Ⅱ）时，的可能取值为0、1、2、3；

时，的可能取值为0、1、2、3；

时，的可能取值为2、3、4；

时，的可能取值为3、4、5、6.

∴.………………………………………………………………12分

20．解：（1） ∵　∴

由已知得　，即 　　　

∴ a=1,b=3　　　……………………6分

　 （2）由（1）知 ∴  

令　解得 x≤－2或x≥0

∴f(x)在区间(－∞,－2 )和[0,+∞]上单调递增

若f(x)在[m-1,m+1] 上单调递增

则　[m-1,m+1] (－∞,－2 )或[m-1,m+1]  [0,+∞]

∴m+1≤－2或 m-1≥0 　∴ m≤－3或 m≥1

所以m的取值范围是m≤－3或 m≥1　　　　…………………12分

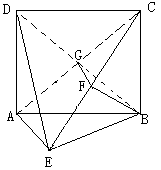21．证明:（1）

………6分

　 （2）（法一）连结AC、BD交于G，连结FG，

∵ABCD为正方形，∴BD⊥AC，∵BF⊥平面ACE，∴FG⊥AC，

∠FGB为二面角B-AC-E的平面角，由（1）可知，AE⊥平面BCE，

∴AE⊥EB，又AE=EB，AB=2，AE=BE=，

在直角三角形BCE中， BE=，CE=

在正方形中，BG=，在直角三角形BFG中，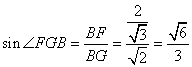

∴二面角B-AC-E为……………………………………………………12分

（法二）向量法：取AB中点为O,连EO, ∵AE=EB，∴EO⊥AB,

∴EO⊥平面ABCD， 以O为原点，OE，AB所在直线分别为x，y

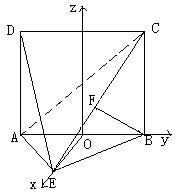轴，建立空间直角坐标系。易知为面ABC的一　个法向量，设 为面ACE的法向量。

∵，，则，

，

　 ，

∴二面角B-AC-E为.

22．（1）解：∵函数的图象关于原点对称

∴为奇函数，

∴

即恒成立

∴b=0，d=0

∵x=1时，f(x)取极小值－，

∴(1)=0，f(1)= －

∴3a+c=0，a+c=－　 ∴a=，c=－1

∴a=，b=0，c=－1，d=0 ……………………………………………………4分

　 （2）解：由（1）有

当x∈[－1，1]时，－1≤x²－1≤0，因而对x₁，x₂∈[－1，1]时，

(x₁) (x₂)≥0

∴当x∈[－1，1]时，f(x)图象上不存在两点，使得过此两点处的切线互相垂直

…………………………8分

　 （3）解：由（2）有函数f(x)在[－1，1]上是减函数

 …………………12分