高三数学上学期质量检测试题
一、选择题(本大题共6小题,每小题5 分,共30分)
1、 已知全集![]() ,集合
,集合![]() ,则
,则![]() 等于
等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、下列函数为奇数函数的是
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3、对于直线![]() 和平面
和平面![]() ,下列命题中,真命题是
,下列命题中,真命题是
A.若![]() ,则
,则![]() B.若
B.若![]() 则
则![]()
C. 若![]() ,则
,则![]() D. 若
D. 若![]() ,则
,则![]()
4、直线![]() 与圆
与圆![]() 有公共点,则常数
有公共点,则常数![]() 的取值范围是
的取值范围是
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5、已知命题![]() :
:![]() ,则命题┐
,则命题┐![]() 是
是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
6、函数![]() (
(![]() )是
)是![]() 上的减函数,则
上的减函数,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
二、填空题(本大题共10小题,每小题5分,共50分,把答案填在题中横线上)
7、计算![]() 的结果是
。
的结果是
。
8、各项均为实数的等比数列![]() 中,
中,![]() ,则
,则![]() 。
。
9、某校共有师生1600人,其中教师有100人,现用分层抽样的方法,从所有师生中抽取一个容量为80的样本,则抽取的学生为 。
10、已知向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() ,则
,则 ![]() 。
。
11、一只蚂蚁在三边边长分别为3,4,5的三角形的边上爬行,某时刻该蚂蚁距离三角形的三个顶点的距离均超过![]() 的概率为
。
的概率为
。
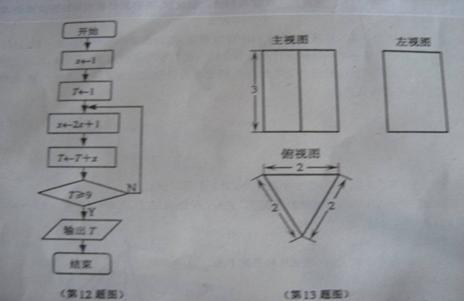
12、根据如图所示的算法流程图,可知输出的结果![]() 为
。
为
。
13、已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:![]() ),可得这个几何体的表面积是
。
),可得这个几何体的表面积是
。
14、已知实数![]() 满足约束条件
满足约束条件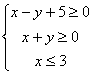 则
则 ![]() 的最小值为
。
的最小值为
。
15、设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 绕原点按逆时针方向旋转
绕原点按逆时针方向旋转![]() 得到直线
得到直线![]() ,则
,则![]() 的方程是
。
的方程是
。
16、设函数![]() 的图象位于
的图象位于![]() 轴右侧所有的对称中心从左依次为
轴右侧所有的对称中心从左依次为![]() ,则
,则
![]() 的坐标是
。
的坐标是
。
二、解答题
17、(本题满分12分,第1小题8分,第2小题4分)
已知函数![]()
(1)
求函数![]() 的周期;
的周期;
(2)
函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
18、(本题满分12分)
要建一间地面面积为20![]() ,墙高为
,墙高为![]() 的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元
的长方形储藏室,在四面墙中有一面安装一扇门(门的面积和墙面的面积按一定的比例设计)。已知含门一面的平均造价为300元![]() ,其余三面的造价为200元
,其余三面的造价为200元![]() ,屋顶的造价为250元
,屋顶的造价为250元![]() 。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
。问怎样设计储藏室地面矩形的长与宽,能使总价最低,最低造价是多少?
 19、(本题满分12分,第1小题3分,第2小题4分,第3小题5分)
19、(本题满分12分,第1小题3分,第2小题4分,第3小题5分)
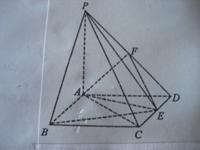
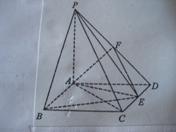
如图,在四棱锥![]() 中,ABCD是矩形,
中,ABCD是矩形,![]() ,
,![]() ,
,
点![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上移动。
上移动。
(1)
求三棱锥![]() 体积;
体积;
(2)
当点![]() 为
为![]() 的中点时,试判断
的中点时,试判断![]() 与平面
与平面![]() 的关系,并说明理由;
的关系,并说明理由;
(3)
求证:![]()
20、(本题满分14分,第1小题4分,第2小题5分,第3小题5分)
已知各项均为正数的数列![]() 中,
中,![]() 是数列
是数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,有
,有
![]()
(1)
求常数![]() 的值;
的值;
(2)
求数列![]() 的通项公式;
的通项公式;
(3)
记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() 。
。
21、(本题满分14分,第1小题5分,第2小题9分)
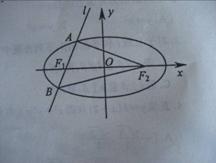 如图,椭圆
如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点。
两点。
(1)
若![]() ,且
,且 ![]() 求椭圆的离心率。
求椭圆的离心率。
(2)
若![]() ,求
,求![]() 的最大值和最小值。
的最大值和最小值。
22、(本题满分16分,第1小题8分,第2小题8分)
设函数![]() ,
,![]() ,当
,当![]() 时,
时,![]() 取得极值。
取得极值。
(1)
求![]() 的值,并判断
的值,并判断![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(2)
当![]() 时,函数
时,函数![]() 与
与![]() 的图象有两个公共点,求
的图象有两个公共点,求![]() 的取值范围。
的取值范围。
参考答案
一、选择题(本大题共6小题,每小题5 分,共30分)
ABDADB
二、填空题(本大题共10小题,每小题5分,共50分,把答案填在题中横线上)
7、![]() ;8、
;8、![]() ;9、75;10、
;9、75;10、![]() ;11、
;11、![]() ;12、11;13、
;12、11;13、![]() ;
;
14、![]() ;15、
;15、![]() ;16、
;16、![]()
三、解答题
17、解:(1)![]()
![]()
所以 函数![]() 的周期是
的周期是![]() ………………………………………………8分
………………………………………………8分
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再将所得图象上每一点的横坐标变为原来的
个单位,再将所得图象上每一点的横坐标变为原来的![]() 倍(纵坐标不变式),得函数
倍(纵坐标不变式),得函数![]() 的图象………………………12分。
的图象………………………12分。
18、解:设地面矩形在门正下方的一边长为![]() ,则另一边的长为
,则另一边的长为![]() ………2分
………2分
设总造价为![]() 元,则
元,则
![]() …………………………………………………………………………………7分
…………………………………………………………………………………7分
因为 ![]()
当且仅当![]() (
(![]() 即
即![]() 时 取“=”…………………………9分
时 取“=”…………………………9分
所以,当![]() 时
时![]() 有最小的值
有最小的值![]() 此时
此时![]() ……………………11分
……………………11分
答:当储藏室地面矩形在门正下方的一边长为![]() ,另一边的长为
,另一边的长为![]() 时,能使总造价最低造价为17000元。……………………………………………………12分。
时,能使总造价最低造价为17000元。……………………………………………………12分。
19、解:(1)![]()
![]() ,
,
![]() …………3分
…………3分
(2)当点![]() 为
为![]() 的中点时,
的中点时,![]() 。…………4分
。…………4分
理由如下:![]() 点
点![]() 分别为
分别为![]() 、PD的中点,
、PD的中点,
![]()
![]() 。
。
![]()
![]() ,
,![]()
![]() …………………………………………7分
…………………………………………7分
(3)![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]() ,
,![]()
![]()
![]() …………………………………10分
…………………………………10分
![]() ,点
,点![]() 是
是![]() 的中点
的中点 ![]()
又![]()
![]()
![]()
![]() ………………………………12分
………………………………12分
20、解:(1)由![]() 及
及![]() ,得:
,得:
![]()
![]() ……………………………………………………4分
……………………………………………………4分
(2)由![]() ①
①
得![]() ②
②
由②—①,得
![]()
即:![]()
![]()
由于数列![]() 各项均为正数,
各项均为正数,
![]() 即
即 ![]() ……………………………………6分
……………………………………6分
![]() 数列
数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,
的等差数列,
![]() 数列
数列![]() 的通项公式是
的通项公式是 ![]() ……………9分
……………9分
(3)由![]() ,得:
,得:![]()
![]() ……………………………………………………11分
……………………………………………………11分
![]()
![]()
![]()
![]()
21、解:(1)![]()
![]() ,
,![]()
![]()
![]() ,
,![]() …………………………3分
…………………………3分
![]() ,
,![]()
![]() ………………………………………5分
………………………………………5分
(2)![]() ,
,![]() 。
。
①若![]() 垂直于
垂直于![]() 轴,则
轴,则![]() ,
,
![]() ,
,
![]()
②若![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为
![]()
由![]() 得
得 ![]()
![]() ,
,![]() 方程有两个不等的实数根。
方程有两个不等的实数根。
设![]() ,
,![]() .
.
![]() ,
, ![]() ………………………………9分
………………………………9分
![]()
![]()
![]()
![]()
=![]() ……………………………………12分
……………………………………12分
![]() …………………………………13分
…………………………………13分
![]() ,所以当直线
,所以当直线![]() 垂于
垂于![]() 轴时,
轴时,![]() 取得最大值
取得最大值![]()
当直线![]() 与
与![]() 轴重合时,
轴重合时,![]() 取得最小值
取得最小值![]() …………………………14分
…………………………14分
22、解:(1)由题意 ![]() ………………………………………………2分
………………………………………………2分
![]() 当
当![]() 时,
时,![]() 取得极值,
取得极值,
![]() 所以
所以 ![]()
![]()
![]() 即
即 ![]() …………………………5分
…………………………5分
此时当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 是函数
是函数![]() 的最小值。………………………………………8分
的最小值。………………………………………8分
(2)设![]() ,则
,则 ![]() ,
,![]() ……10分
……10分
设![]() ,
,![]()
![]() ,令
,令![]() 解得
解得![]() 或
或![]()
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
| __ | 0 | + | ||
|
|
|
|
|
|
|
|
|
![]() 函数
函数![]() 在
在![]() 和
和![]() 上是增函数,在
上是增函数,在![]() 上是减函数。
上是减函数。
当![]() 时,
时,![]() 有极大值
有极大值![]() ;当
;当![]() 时,
时,![]() 有极小值
有极小值![]() ……14分
……14分
![]() 函数
函数![]() 与
与![]() 的图象有两个公共点,
的图象有两个公共点,![]() 函数
函数![]() 与
与![]() 的图象有两个公共点
的图象有两个公共点
![]() 或
或 ![]()
![]()